金融原理/第一部分/第七章/资本资产定价模型

道琼斯工业平均指数在3年内每月数据的CAPM和证券市场线（紫色）的估计。

在金融领域，资本资产定价模型（CAPM）用于确定资产在加入已充分多元化的投资组合时的理论上适当的必要回报率，前提是该资产具有不可分散风险。该模型考虑了资产对不可分散风险的敏感性（也称为系统性风险或市场风险），金融行业通常用β（β）表示，以及市场的预期回报和理论无风险资产的预期回报。

该模型由Jack Treynor（1961，1962）、 William Sharpe（1964）、John Lintner（1965a，b）和Jan Mossin（1966）独立提出，其基础是Harry Markowitz早期的多元化和现代投资组合理论研究。Sharpe、Markowitz和Merton Miller因对金融经济学领域的贡献而共同获得了诺贝尔经济学奖。

公式

文件:SecMktLine.png 证券市场线，如图形所示，描述了β与资产预期回报率之间的关系。

CAPM是用于对单个证券或投资组合进行定价的模型。对于单个证券，我们利用证券市场线 (SML) 及其与预期回报和系统性风险 (β) 之间的关系来表明市场必须如何根据其安全风险类别对单个证券进行定价。SML 使我们能够计算任何证券的风险回报率与整个市场的风险回报率之间的关系。因此，当任何证券的预期回报率除以其β系数时，市场中任何单个证券的风险回报率等于市场风险回报率，因此

${\frac {E(R_{i})-R_{f}}{\beta _{i}}}=E(R_{m})-R_{f}$

市场风险回报率实际上是市场风险溢价，通过重新排列上面的等式并求解E(Ri)，我们得到了资本资产定价模型 (CAPM)。

$E(R_{i})=R_{f}+\beta _{i}(E(R_{m})-R_{f})\,$

其中

• $E(R_{i})~~$是资本资产的预期回报
• $R_{f}~$是无风险利率，例如政府债券产生的利息
• $\beta _{i}~~$（beta）是预期超额资产回报对预期超额市场回报的敏感性，或者$\beta _{i}={\frac {\mathrm {Cov} (R_{i},R_{m})}{\mathrm {Var} (R_{m})}}$,
• $E(R_{m})~$是市场的预期回报
• $E(R_{m})-R_{f}~$有时被称为市场溢价（预期市场回报率与无风险回报率之间的差值）。
• $E(R_{i})-R_{f}~$ 也被称为 *风险溢价*。

换句话说，从风险溢价的角度来看，我们发现

$E(R_{i})-R_{f}=\beta _{i}(E(R_{m})-R_{f})\,$

这表明 *个体风险溢价* 等于 *市场溢价* 乘以 *β*。

注意 1：市场预期回报率通常通过测量市场投资组合（例如标准普尔 500 指数）的历史回报的几何平均值来估算。

注意 2：用于确定风险溢价的无风险回报率通常是历史无风险回报率的算术平均值，而不是当前无风险回报率。

有关完整的推导，请参见现代投资组合理论。

证券市场线

SML 本质上是资本资产定价模型 (CAPM) 公式结果的图表。*x* 轴代表风险 (beta)，*y* 轴代表预期回报。市场风险溢价由 SML 的斜率决定。

β 和要求回报之间的关系绘制在 *证券市场线* (SML) 上，该线显示了预期回报作为 β 的函数。截距是市场上可获得的名义无风险利率，而斜率是市场溢价，E(R_m)− R_f。证券市场线可以被视为代表资产价格的单因素模型，其中 Beta 是对市场价值变化的敞口。因此，SML 的方程式为

$\mathrm {SML} :E(R_{i})=R_{f}+\beta _{i}(E(R_{M})-R_{f}).~$

这是一个有用的工具，用于确定正在考虑纳入投资组合的资产是否提供了合理的风险预期回报。单个证券绘制在 SML 图表上。如果证券的预期回报与风险绘制在 SML 以上，则该证券被低估，因为投资者可以预期从固有的风险中获得更高的回报。而绘制在 SML 以下的证券被高估，因为投资者会接受较低的回报以换取承担的风险。

资产定价

一旦使用 CAPM 计算出预期/要求回报率，$E(R_{i})$，我们可以将此要求回报率与资产在特定投资期限内的估计回报率进行比较，以确定其是否为合适的投资。要进行此比较，您需要根据 **基本面分析或技术分析技术**（包括市盈率、市净率等）对证券的回报前景进行独立估计。

假设 CAPM 是正确的，当估计价格与资产未来现金流的现值相同时，资产的价格是正确的，该现值以 CAPM 建议的比率贴现。如果估计价格高于 CAPM 估值，则该资产被低估（而当估计价格低于 CAPM 估值时被高估）。 当资产不在 SML 上时，这也可能表明定价错误。由于资产在时间 $t$ 的预期回报是 $E(R_{t})={\frac {E(P_{t+1})-P_{t}}{P_{t}}}$，比 CAPM 建议的预期回报率更高表明 $P_{t}$ 太低（该资产目前被低估），假设在时间 $t+1$ 该资产恢复到 CAPM 建议的价格。

使用 CAPM 的资产价格 $P_{0}$，有时被称为确定性等价定价公式，是一个线性关系，由下式给出

$P_{0}={\frac {1}{1+R_{f}}}\left[E(P_{T})-{\frac {\mathrm {Cov} (P_{T},R_{M})(E(R_{M})-R_{f})}{\mathrm {Var} (R_{M})}}\right]$

其中 $P_{T}$ 是资产或投资组合的收益。

资产特定要求回报

CAPM 返回资产适当的必要回报或折现率，即考虑到资产的相对风险性，应按该比率折现资产产生的未来现金流。高于 1 的贝塔系数表示风险高于平均水平；低于 1 的贝塔系数表示风险低于平均水平。因此，风险较高的股票将具有更高的贝塔系数，并以更高的比率折现；风险较低的股票将具有较低的贝塔系数，并以较低的比率折现。鉴于公认的凹型效用函数，CAPM 与直觉一致 - 投资者（应该）要求更高的回报来持有风险较高的资产。

由于贝塔系数反映了资产对不可分散的（即市场）风险的特定敏感性，因此整个市场（按定义）的贝塔系数为 1。股票市场指数通常用作市场的局部代理 - 在这种情况下（按定义）贝塔系数为 1。因此，一个大型多元化投资组合（如共同基金）的投资者预计表现将与市场一致。

风险和多元化

投资组合的风险包括系统性风险（也称为不可分散风险）和非系统性风险（也称为特质风险或可分散风险）。系统性风险是指所有证券共有的风险，即市场风险。非系统性风险是与单个资产相关的风险。通过在投资组合中包含更多资产，非系统性风险可以分散到更小的水平（特定风险“平均化”)。在一个市场内，系统性风险无法以同样的方式分散。根据市场的不同，在英国或美国等发达市场，一个大约 30-40 种证券的投资组合将使投资组合充分多元化，以至于风险敞口仅限于系统性风险。在发展中国家，由于资产波动性较高，需要更多数量的证券。

理性的投资者不应该承担任何可分散的风险，因为在这个模型的范围内，只有不可分散的风险才会得到回报。因此，资产的必要回报，即补偿所承担风险的回报，必须与它在投资组合中的风险性相关联 - 即它对整体投资组合风险性的贡献 - 而不是它“独立风险性”。在 CAPM 的背景下，投资组合风险用更高的方差（即更低的可预测性）来表示。换句话说，投资组合的贝塔系数是衡量投资者承担的系统性敞口回报的决定因素。

有效边界

(马科维茨) 有效边界。CAL 代表资本配置线。

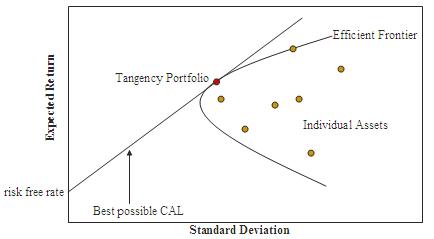
CAPM 假设投资组合的风险回报状况可以优化 - 最佳投资组合在回报水平方面显示出最低可能的风险水平。此外，由于添加到投资组合中的每项额外资产都会进一步分散投资组合，因此最佳投资组合必须包含所有资产（假设没有交易成本），并且每个资产的价值加权以实现上述目标（假设任何资产都是无限可分的）。所有这些最佳投资组合，即每个回报水平的一个，构成有效边界。

由于非系统性风险是可分散的，因此投资组合的总风险可以视为贝塔系数。

市场投资组合

投资者可以选择将其财富的一部分投资于风险资产组合，其余部分投资于现金 - 以无风险利率赚取利息（或者实际上可以借钱来为其购买风险资产提供资金，在这种情况下，现金权重为负）。在这里，风险资产与无风险资产的比例不决定总回报 - 这种关系显然是线性的。因此，可以通过两种方式实现特定回报

1. 将全部财富投资于风险投资组合，
2. 或将一部分投资于风险投资组合，其余部分投资于现金（借入或投资）。

然而，对于给定的回报水平，这些投资组合中只有一个是最优的（从最低风险的角度而言）。由于无风险资产（按定义）与任何其他资产不相关，因此选项 2 通常具有较低的方差，因此是两种选项中更有效的一个。

这种关系也适用于有效边界上的投资组合：对于较低的回报水平，较高回报投资组合加上现金比仅有较低回报投资组合更有效。对于给定的无风险利率，只有一个最优投资组合可以与现金相结合，以在任何可能的回报下实现最低的风险水平。这就是市场投资组合。

CAPM 的假设

所有投资者： Template:Unreferenced section

1. 旨在最大化经济效用。
2. 是理性的，并且厌恶风险。
3. 在各种投资中实现广泛多元化。
4. 是价格接受者，即他们无法影响价格。
5. 可以以无风险利率借入和借出无限金额。
6. 在没有交易或税收成本的情况下进行交易。
7. 处理所有可高度分割成小部分的证券。
8. 假设所有信息都同时提供给所有投资者。

此外，该模型假设过去回报的标准差是与给定证券相关的未来风险的完美替代指标。

CAPM 的问题

• 该模型假设回报的方差是风险的充分衡量指标。这将由回报呈正态分布的假设所暗示，或者确实，以任何双参数方式分布，但对于一般的回报分布，其他风险衡量指标（如相干风险衡量指标）将更充分地反映活跃和潜在股东的偏好。事实上，金融投资中的风险本身并不是方差，而是亏损的可能性：它本质上是不对称的。
• 该模型假设所有活跃和潜在股东都能获得相同的信息，并且同意所有资产的风险和预期回报（同质预期假设）。
• 该模型假设活跃和潜在股东的概率信念与回报的真实分布相匹配。另一种可能性是，活跃和潜在股东的预期是有偏见的，导致市场价格信息效率低下。这种可能性在行为金融领域被研究，该领域使用心理假设来提供 CAPM 的替代方案，例如肯特·丹尼尔、大卫·希尔斯利弗和阿瓦尼达尔·苏布拉马尼亚姆（2001 年）的过度自信资产定价模型。
• 该模型似乎无法充分解释股票回报的变化。实证研究表明，低贝塔系数股票可能比模型预测的提供更高的回报。这种数据最早在 1969 年纽约布法罗的一次会议上由菲舍尔·布莱克、迈克尔·詹森和迈伦·斯科尔斯在一篇论文中提出。要么这个事实本身是理性的（这将拯救有效市场假说，但使 CAPM 错误），要么它是不理性的（这将拯救 CAPM，但使 EMH 错误 - 事实上，这种可能性使波动率套利成为可靠地击败市场的一种策略）。
• 该模型假设，在给定的预期回报下，活跃和潜在股东会更倾向于较低的风险（较低的方差）而不是较高的风险，反之亦然，在给定的风险水平下，会更倾向于较高的回报而不是较低的回报。它不允许存在愿意为更高风险接受较低回报的活跃和潜在股东。赌场赌徒付费以承担更多风险，并且有可能一些股票交易者也会为风险付费。
• 该模型假设没有税收或交易成本，尽管这个假设可以通过更复杂的模型版本来放宽。
• 市场投资组合由所有市场中的所有资产组成，其中每个资产的权重与其市值成正比。这假设个人活跃和潜在股东对市场和资产没有偏好，并且活跃和潜在股东仅根据其风险回报状况选择资产。它还假设所有资产都是无限可分的，可以持有或交易的量没有限制。
• 理论上，市场组合应该包含所有由任何人作为投资持有的资产类型（包括艺术品、房地产、人力资本等等）。实际上，这种市场组合是不可观察的，人们通常用股票指数来代替真实的市场组合。不幸的是，已经证明这种替代并非无害，它会导致对资本资产定价模型有效性的错误推断，并有人指出，由于真实市场组合的不可观察性，资本资产定价模型可能无法在经验上进行检验。这在理查德·罗尔 1977 年发表的一篇论文中得到了更深入的论述，通常被称为罗尔批判。
• 该模型假设经济主体在短期内进行优化，事实上，具有长期视野的投资者会最优地选择长期通胀挂钩债券而不是短期利率，因为对于这样的主体来说，这将是更无风险的资产。
• 该模型只假设两个日期，因此没有机会随着时间的推移反复消费和重新平衡投资组合。该模型的基本见解在罗伯特·默顿的跨期资本资产定价模型（ICAPM） 和道格拉斯·布里登和马克·鲁宾斯坦的消费资本资产定价模型（CCAPM） 中得到了扩展和推广。
• CAPM 假设所有活跃的和潜在的股东都会考虑他们所有的资产并优化一个投资组合。这与个人股东持有的投资组合形成鲜明对比：人类往往拥有分散的投资组合，或者更确切地说，是多个投资组合：每个目标一个投资组合——参见行为投资组合理论 和马斯洛投资组合理论。
• 实证检验表明市场存在诸如规模效应和价值效应之类的异常现象，这些现象无法用 CAPM 解释。 更多详情请参见法玛-弗兰奇三因子模型。

参考文献

• Black, Fischer., Michael C. Jensen, 和 Myron Scholes (1972)。资本资产定价模型：一些实证检验，第 79–121 页，M. Jensen 编辑，《资本市场理论研究》。纽约：普莱格出版社。
• Fama, Eugene F. (1968)。风险、收益和均衡：一些澄清性评论。金融杂志第 23 卷，第 1 期，第 29–40 页。
• Fama, Eugene F. 和 Kenneth French (1992)。预期股票收益的横截面。金融杂志，1992 年 6 月，427-466。
• French, Craig W. (2003)。Treynor 资本资产定价模型，投资管理杂志，第 1 卷，第 2 期，第 60–72 页。可在 http://www.joim.com/ 获取。
• French, Craig W. (2002)。Jack Treynor 的“关于风险资产的市场价值理论”（12 月）。可在 http://ssrn.com/abstract=628187 获取。
• Lintner, John (1965)。风险资产的估值以及股票投资组合和资本预算中风险投资的选择，经济学与统计学评论，47 (1)，13-37。
• Markowitz, Harry M. (1999)。投资组合理论的早期历史：1600-1960，金融分析师杂志，第 55 卷，第 4 期。
• Mehrling, Perry (2005)。Fischer Black 和金融的革命性思想。霍博肯：约翰·威利父子公司。
• Mossin, Jan. (1966)。资本资产市场的均衡，计量经济学，第 34 卷，第 4 期，第 768–783 页。
• Ross, Stephen A. (1977)。资本资产定价模型 (CAPM)、卖空限制及相关问题，金融杂志，32 (177)
• Rubinstein, Mark (2006)。投资理论史。霍博肯：约翰·威利父子公司。
• Sharpe, William F. (1964)。资本资产价格：风险条件下市场均衡理论，金融杂志，19 (3)，425-442
• Stone, Bernell K. (1970) 风险、收益和均衡：资产选择和资本市场均衡的通用单期理论。剑桥：麻省理工学院出版社。
• Tobin, James (1958)。流动性偏好作为对风险的态度，经济研究评论，25
• Treynor, Jack L. (1961)。市场价值、时间和风险。未出版手稿。
• Treynor, Jack L. (1962)。关于风险资产的市场价值理论。未出版手稿。最终版本发表于 1999 年，收录于资产定价和投资组合表现：模型、策略和表现指标。罗伯特·A·科拉奇克（编辑）伦敦：风险书籍，第 15–22 页。
• Mullins, David W. (1982)。资本资产定价模型有效吗？，哈佛商业评论，1982 年 1 月至 2 月，105-113。

外部链接

• 多资产有效边界