金融原理/第 1 部分/第 7 章/现代投资组合理论

现代投资组合理论（MPT）是一种金融理论，它试图通过仔细选择各种资产的比例来最大化给定投资组合风险的投资组合预期收益，或者等效地最小化给定预期收益水平的风险。 虽然 MPT 在金融行业被广泛使用，并且它的几位创立者因该理论获得了诺贝尔经济学奖， 但近年来，行为经济学等领域的学者对 MPT 的基本假设提出了广泛的质疑。

MPT 是投资多元化概念的数学表达形式，其目标是选择一个投资资产组合，该组合的整体风险低于任何单个资产。直观地可以看出，这是可能的，因为不同类型的资产价格变化往往是相反的。 例如，在一定程度上，股票市场的价格与债券市场的价格变化不同，因此，理论上，包含这两种类型资产的集合可以承受比任何单独资产都低的总体风险。但即使资产的回报不呈负相关，多元化也能降低风险——事实上，即使它们呈正相关也是如此。

更准确地说，MPT 将资产的回报建模为正态分布函数（或更一般地，为椭圆分布随机变量），将风险定义为回报的标准差，并将投资组合建模为资产的加权组合，因此，投资组合的回报是资产回报的加权组合。通过组合回报不完全正相关的不同资产，MPT 试图降低投资组合回报的总方差。MPT 还假设投资者是理性的，市场是有效的。

MPT 在 1950 年代至 1970 年代初发展起来，被认为是金融数学建模领域的一项重大进展。从那时起，它受到了许多理论和实践上的批评。这些批评包括：金融回报不遵循高斯分布，也不遵循任何对称分布；资产类别之间的相关性并非固定，而是会根据外部事件（尤其是在危机时期）而变化。此外，越来越多的证据表明，投资者并不理性，市场并不有效。

概念

MPT 背后的基本概念是，投资组合中的资产不应单独选择，每个资产都具有自己的优点。相反，重要的是要考虑每个资产的价格变化相对于投资组合中所有其他资产的价格变化。

投资是风险和预期回报之间的权衡。一般来说，预期回报更高的资产风险更大。对于给定的风险量，MPT 描述了如何选择预期回报最高的投资组合。或者，对于给定的预期回报，MPT 解释了如何选择风险最低的投资组合（目标预期回报当然不能超过可投资的最高回报证券，除非可以进行负资产持仓）。

因此，MPT 是一种多元化形式。在某些假设下，对于风险和回报的特定量化定义，MPT 解释了如何找到最佳的多元化策略。

历史

Harry Markowitz 在 1952 年的一篇文章 和 1959 年的一本书中介绍了 MPT。 Markowitz 称之为“投资组合理论”，因为“它本身并不现代”。另请参见此 历史调查。

数学模型

在某种意义上，下面推导的数学公式就是MPT，尽管模型背后的基本概念也很有影响力。

本节介绍“经典”的 MPT 模型。此后，该模型进行了许多扩展。

风险和预期收益

MPT 假设投资者是风险厌恶的，这意味着给定两个提供相同预期回报的投资组合，投资者会选择风险较小的那个。因此，投资者只有在获得更高的预期回报时才会承担更高的风险。反之，想要获得更高预期回报的投资者必须接受更高的风险。所有投资者的精确权衡都是一样的，但不同的投资者会根据个人风险厌恶特征对权衡进行不同的评估。这意味着，理性的投资者不会投资于一个投资组合，如果存在另一个投资组合具有更优的风险-预期回报特征——也就是说，对于该风险水平，存在一个具有更好预期回报的替代投资组合。

请注意，该理论使用回报的标准差来代替风险，这在资产回报是联合正态分布或其他椭圆分布的情况下是有效的。然而，这方面存在问题；请参阅批评部分。

在该模型下

• 投资组合回报是组成资产回报的比例加权组合。
• 投资组合波动率是组成资产相关性ρ_ij的函数，对于所有资产对 (i, j) 来说都是如此。

一般来说

• 预期回报

$\operatorname {E} (R_{p})=\sum _{i}w_{i}\operatorname {E} (R_{i})\quad$

其中 $R_{p}$ 是投资组合的收益率，$R_{i}$ 是资产 i 的收益率，$w_{i}$ 是构成资产 $i$ 的权重（即资产 i 在投资组合中的比例）。

• 投资组合收益率方差

$\sigma _{p}^{2}=\sum _{i}w_{i}^{2}\sigma _{i}^{2}+\sum _{i}\sum _{j\neq i}w_{i}w_{j}\sigma _{i}\sigma _{j}\rho _{ij},$

其中 $\rho _{ij}$ 是资产 i 和 j 收益率之间的相关系数。或者，表达式可以写成

$\sigma _{p}^{2}=\sum _{i}\sum _{j}w_{i}w_{j}\sigma _{i}\sigma _{j}\rho _{ij}$,

其中 $\rho _{ij}=1$ 当 i=j 时。

• 投资组合收益率波动率（标准差）

$\sigma _{p}={\sqrt {\sigma _{p}^{2}}}$

对于一个包含两种资产的投资组合

• 投资组合收益率：$\operatorname {E} (R_{p})=w_{A}\operatorname {E} (R_{A})+w_{B}\operatorname {E} (R_{B})=w_{A}\operatorname {E} (R_{A})+(1-w_{A})\operatorname {E} (R_{B}).$
• 投资组合方差：$\sigma _{p}^{2}=w_{A}^{2}\sigma _{A}^{2}+w_{B}^{2}\sigma _{B}^{2}+2w_{A}w_{B}\sigma _{A}\sigma _{B}\rho _{AB}$

对于一个包含三种资产的投资组合

• 投资组合收益率：$w_{A}\operatorname {E} (R_{A})+w_{B}\operatorname {E} (R_{B})+w_{C}\operatorname {E} (R_{C})$
• 投资组合方差: $\sigma _{p}^{2}=w_{A}^{2}\sigma _{A}^{2}+w_{B}^{2}\sigma _{B}^{2}+w_{C}^{2}\sigma _{C}^{2}+2w_{A}w_{B}\sigma _{A}\sigma _{B}\rho _{AB}+2w_{A}w_{C}\sigma _{A}\sigma _{C}\rho _{AC}+2w_{B}w_{C}\sigma _{B}\sigma _{C}\rho _{BC}$

多元化

投资者可以通过持有不完全正相关（相关系数 $-1\leq \rho _{ij}<1$）的组合工具来降低投资组合风险。换句话说，投资者可以通过持有多元化的资产组合来降低其对单个资产风险的敞口。多元化可能允许在降低风险的情况下获得相同的投资组合预期收益。这些想法最初是由马科维茨提出的，后来得到了其他经济学家和数学家（如安德鲁·布伦南）的认可，他们在投资组合理论中表达了通过多元化减少方差的想法。

如果所有资产对的相关性都为 0——它们完全不相关——那么投资组合的收益方差是所有资产的收益方差平方与该资产持有比例平方的总和（投资组合标准差是该总和的平方根）。

没有无风险资产的有效边界

有效边界。双曲线有时被称为“马科维茨子弹”，如果不存在无风险资产，则是有效边界。如果存在无风险资产，则直线是有效边界。

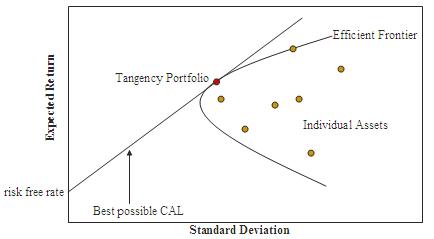
如该图所示，不包括任何无风险资产的任何可能的风险资产组合，都可以在风险-预期收益空间中绘制，所有这些可能组合的集合定义了该空间中的一个区域。该区域的左边界是双曲线， 该区域的上边缘是在没有无风险资产的情况下（有时被称为“马科维茨子弹”）的有效边界。沿着该上边缘的组合代表投资组合（包括没有无风险资产的持有），这些投资组合在给定预期收益水平下具有最低风险。等效地，位于有效边界上的投资组合代表在给定风险水平下提供最佳可能预期收益的组合。

矩阵更适合计算有效边界。

以矩阵形式，对于给定的“风险承受能力” $q\in [0,\infty )$，有效边界可以通过最小化以下表达式找到

$w^{T}\Sigma w-q*R^{T}w$

其中

• $w$ 是投资组合权重的向量，并且 $\sum _{i}w_{i}=1.$（权重可以为负，这意味着投资者可以卖空证券）；
• $\Sigma$ 是投资组合中资产收益的协方差矩阵；
• $q\geq 0$ 是一个“风险承受能力”因子，其中 0 会导致风险最小的投资组合，而 $\infty$ 会导致投资组合无限地延伸到边界，预期收益和风险都无界；以及
• $R$ 是预期收益的向量。
• $w^{T}\Sigma w$ 是投资组合收益的方差。
• $R^{T}w$ 是投资组合的预期收益。

上述优化找到了边界上的一个点，在这个点上，如果投资组合收益方差而不是标准差在水平方向上绘制，则边界的斜率的倒数将是q。边界整体上是关于q参数化的。

许多软件包（包括 MATLAB、Microsoft Excel、Mathematica 和 R）都提供适合上述问题的优化例程。

确定有效边界的一种替代方法是按预期投资组合收益$R^{T}w.$进行参数化。这种问题的版本要求我们最小化

$w^{T}\Sigma w$

受制于

$R^{T}w=\mu$

参数$\mu$。这个问题可以使用拉格朗日乘子轻松解决。

两个共同基金定理

上述分析的一个关键结果是两个共同基金定理。 该定理指出，有效边界上的任何投资组合都可以通过持有边界上任意两个给定投资组合的组合来生成；后两个给定投资组合是定理名称中的“共同基金”。因此，在没有无风险资产的情况下，即使投资者只能获得一对有效共同基金，也可以实现任何所需的有效投资组合。如果所需投资组合在有效边界上的位置位于两个共同基金位置之间，则将以正量持有这两个共同基金。如果所需投资组合位于两个共同基金跨越的范围之外，则必须卖空其中一个共同基金（以负量持有），而对另一个共同基金的投资规模必须大于可供投资的金额（超出部分由从另一个基金借款提供资金）。

无风险资产和资本配置线

无风险资产是（假设的）资产，它支付无风险利率。在实践中，短期政府债券（例如美国国库券）被用作无风险资产，因为它们支付固定利率，并且违约风险极低。无风险资产的收益方差为零（因此是无风险的）；它也与任何其他资产不相关（根据定义，因为它的方差为零）。因此，当它与任何其他资产或资产组合组合时，当组合中的比例发生变化时，收益的变化与风险的变化呈线性关系。

当引入无风险资产时，图中所示的半直线是新的有效边界。它在具有最高夏普比率的纯风险投资组合处与双曲线相切。它的水平截距表示一个投资组合，其 100% 的持仓为无风险资产；与双曲线的切线表示一个投资组合，其无风险持仓为 0%，所有资产都持有发生在切点处的投资组合；这些点之间的点是包含正量风险切线投资组合和无风险资产的投资组合；半直线超出切点处的点是杠杆投资组合，涉及无风险资产的负持仓（后者被卖空——换句话说，投资者以无风险利率借款），并且投资于切线投资组合的金额超过投资者的初始资金的 100%。这个有效的半直线被称为资本配置线 (CAL)，它的公式可以证明为

$E(R_{C})=R_{F}+\sigma _{C}{\frac {E(R_{P})-R_{F}}{\sigma _{P}}}.$

在这个公式中，P 是与马科维茨弹丸相切的风险资产子投资组合，F 是无风险资产，C 是投资组合 P 和 F 的组合。

从图中可以看出，将无风险资产引入作为投资组合可能组成部分，提高了可用风险-预期收益组合的范围，因为除了切线投资组合以外，半直线在每个可能的风险水平上都比双曲线提供更高的预期收益。所有线性有效轨迹上的点都可以通过持有无风险资产和切线投资组合的组合来实现，这一事实被称为一个共同基金定理。，其中提到的共同基金是切线投资组合。

使用 MPT 进行资产定价

上述分析描述了个人投资者的最优行为。资产定价理论以如下方式建立在这个分析的基础上。由于每个人都以相同比例持有风险资产——即切线投资组合中给出的比例——在市场均衡状态下，风险资产的价格，因此它们的预期收益将进行调整，以使切线投资组合中的比率与风险资产供应给市场的比率相同。因此，相对供应将等于相对需求。MPT 在这种情况下推导出正确定价资产的所需预期收益。

系统性风险和特有风险

特有风险与单个资产相关联 - 在投资组合中，这些风险可以通过多元化来降低（特有风险“抵消”）。特有风险也称为可分散风险、独特风险、非系统性风险或特质风险。系统性风险（又名投资组合风险或市场风险）是指所有证券共有的风险——除了卖空外，系统性风险无法通过分散投资消除（在一个市场内）。在市场投资组合中，资产特有风险将在最大程度上通过分散投资消除。因此，系统性风险等同于市场投资组合的风险（标准差）。

由于只有当证券能够改善市场投资组合的风险-预期收益特征时，才会购买该证券，因此，衡量证券风险的适当指标是它添加到市场投资组合中的风险，而不是孤立的风险。在这种情况下，资产的波动性及其与市场投资组合的相关性是根据历史观察得出的，因此是已知的。（有几种资产定价方法试图通过对资产收益的矩的随机属性进行建模来对资产进行定价——这些方法通常被称为条件资产定价模型。）

可以通过在单个投资组合中使用多头和空头头寸的策略来管理一个市场中的系统性风险，从而创建一个“市场中性”投资组合。

资本资产定价模型

资产收益取决于今天支付的资产金额。支付的价格必须确保在将资产添加到市场组合时，市场组合的风险/收益特征得到改善。CAPM 模型推导出资产在市场中的理论必要预期收益（即折现率），该模型考虑了投资者可获得的无风险利率以及整个市场的风险。CAPM 通常表示为

$\operatorname {E} (R_{i})=R_{f}+\beta _{i}(\operatorname {E} (R_{m})-R_{f})$

• $\beta$，即贝塔系数，是衡量资产对整体市场变动敏感程度的指标；贝塔系数通常通过对历史数据的回归分析得出。贝塔系数大于 1 表示资产对整体投资组合风险的贡献大于平均水平；贝塔系数小于 1 表示资产对整体投资组合风险的贡献低于平均水平。

• $(\operatorname {E} (R_{m})-R_{f})$ 是市场溢价，即市场组合预期收益超过无风险利率的预期超额收益。

可以使用以下回归方程对该方程进行统计估计

$\mathrm {SCL} :R_{i,t}-R_{f}=\alpha _{i}+\beta _{i}\,(R_{M,t}-R_{f})+\epsilon _{i,t}{\frac {}{}}$

其中 α_i 称为资产的阿尔法，β_i 是资产的贝塔系数，SCL 是证券特征线。

一旦使用 CAPM 计算出资产的预期收益，$E(R_{i})$，可以使用该比率将资产的未来现金流折现到现值，以确定资产的正确价格。风险较高的股票将具有较高的贝塔系数，并以较高的比率折现；风险敏感度较低的股票将具有较低的贝塔系数，并以较低的比率折现。理论上，当资产的观察价格与其使用 CAPM 推导出的折现率计算出的价值相同，则该资产的定价是合理的。如果观察价格高于估值，则该资产被高估；如果价格过低，则被低估。

（1）在将额外的风险资产 a 添加到市场组合 m 中时，风险和预期收益的增量影响遵循双资产投资组合的公式。这些结果用于推导出适用于资产的折现率。

• 市场组合的风险 = $(w_{m}^{2}\sigma _{m}^{2}+[w_{a}^{2}\sigma _{a}^{2}+2w_{m}w_{a}\rho _{am}\sigma _{a}\sigma _{m}])$

因此，添加到投资组合的风险 = $[w_{a}^{2}\sigma _{a}^{2}+2w_{m}w_{a}\rho _{am}\sigma _{a}\sigma _{m}]$

但由于资产的权重相对较低，$w_{a}^{2}\approx 0$

即新增风险 = $[2w_{m}w_{a}\rho _{am}\sigma _{a}\sigma _{m}]\quad$

• 市场组合的预期收益 = $(w_{m}\operatorname {E} (R_{m})+[w_{a}\operatorname {E} (R_{a})])$

因此，额外的预期收益 = $[w_{a}\operatorname {E} (R_{a})]$

(2) 如果一项资产 a 的价格被正确定价，那么将其添加到市场组合 m 中所带来的风险收益比改善将至少与将这些资金投入市场组合中所带来的收益相匹配。假设投资者将以无风险利率 $R_{f}$ 借款购买该资产；如果 $\operatorname {E} (R_{a})>R_{f}$，这是合理的。

因此：$[w_{a}(\operatorname {E} (R_{a})-R_{f})]/[2w_{m}w_{a}\rho _{am}\sigma _{a}\sigma _{m}]=[w_{a}(\operatorname {E} (R_{m})-R_{f})]/[2w_{m}w_{a}\sigma _{m}\sigma _{m}]$

也就是说：$[\operatorname {E} (R_{a})]=R_{f}+[\operatorname {E} (R_{m})-R_{f}]*[\rho _{am}\sigma _{a}\sigma _{m}]/[\sigma _{m}\sigma _{m}]$

也就是说：$[\operatorname {E} (R_{a})]=R_{f}+[\operatorname {E} (R_{m})-R_{f}]*[\sigma _{am}]/[\sigma _{mm}]$

$[\sigma _{am}]/[\sigma _{mm}]\quad$ 是“贝塔系数”，$\beta$ 回报—— 资产回报与市场回报之间的协方差除以市场回报的方差—— 即资产价格对市场组合价值变动的敏感度。

批评

尽管在理论上具有重要意义，但现代投资组合理论的批评者质疑它是否是一种理想的投资策略，因为其金融市场模型在许多方面与现实世界不符。

将理论基础转化为可行的投资组合构建算法的努力一直受到技术困难的困扰，这些困难源于原始优化问题相对于可用数据的稳定性。最近的研究表明，当在优化过程中加入正则化约束或惩罚项时，此类不稳定性会消失。

假设

现代投资组合理论的框架对投资者和市场做出了许多假设。一些假设在方程中明确表达，例如使用正态分布对回报进行建模。另一些假设是隐含的，例如忽略税收和交易费用。这些假设没有一个是完全正确的，每一个都在一定程度上损害了现代投资组合理论。

• 投资者对上述优化问题感兴趣（在给定方差的情况下最大化均值）。在现实中，投资者拥有效用函数，这些函数可能对收益分布的高阶矩敏感。为了让投资者使用均值-方差优化，必须假设效用和收益的组合使效用优化问题类似于均值-方差优化问题。没有关于收益假设的二次效用就足够了。另一个假设是使用指数效用和正态分布，如下所述。

• 资产回报是（联合）正态分布随机变量。事实上，人们经常观察到，股票和其他市场的回报并非正态分布。市场中出现的大幅波动（偏离均值的 3 到 6 个标准差）远远超过正态分布假设所预测的。虽然该模型也可以通过假设任何联合椭圆的收益分布来证明，但所有联合椭圆分布都是对称的，而资产收益在经验上并非对称的。

• 资产之间的相关性是固定的，永远不变。相关性取决于基础资产之间的系统性关系，当这些关系发生变化时，相关性也会发生变化。例如，一个国家对另一个国家宣战，或者发生普遍的市场崩溃。在金融危机期间，所有资产往往都会变得正相关，因为它们都会（向下）一起移动。换句话说，现代投资组合理论恰好在投资者最需要保护免受风险时失效。

• 所有投资者都致力于最大化经济效用（换句话说，尽可能多地赚钱，而不考虑任何其他因素）。这是现代投资组合理论所依赖的有效市场假说的一个关键假设。

• 所有投资者都是理性的，并且厌恶风险。这是有效市场假说的另一个假设，但我们现在从行为经济学中了解到，市场参与者并非理性。它不允许“羊群行为”或愿意为更高风险接受更低回报的投资者。赌场赌徒显然会为风险付费，一些股票交易者也可能为风险付费。

• 所有投资者都可以在同一时间获得相同的信息。事实上，现实市场存在信息不对称、内幕交易以及那些比其他人更了解信息的人。此外，估计回报的均值（例如，当在 0 和 T 之间进行子采样时，布朗运动的漂移没有一致的估计量）和协方差矩阵（当资产数量与时期数量同阶时）是困难的统计任务。

• 投资者对可能的回报有准确的概念，即投资者的概率信念与回报的真实分布相匹配。另一种可能性是，投资者的预期是有偏见的，导致市场价格缺乏信息效率。这种可能性在行为金融领域中得到了研究，该领域使用心理假设为资本资产定价模型提供替代方案，例如肯特·丹尼尔、大卫·希尔希利弗和阿瓦尼达尔·苏布拉曼尼安 (2001) 的基于过度自信的资产定价模型。

• 不存在税收或交易成本。真实的金融产品会受到税收和交易成本（例如经纪费用）的影响，考虑这些因素将改变最佳投资组合的构成。这些假设可以通过更复杂的模型来放宽。

• 所有投资者都是价格接受者，即他们的行为不会影响价格。在现实中，单个资产的足够大的出售或购买可能会改变该资产和其他资产（通过需求的交叉弹性）的市场价格。如果市场在他们购买所需证券时移动过快，投资者甚至可能无法组建理论上的最佳投资组合。

• 任何投资者都可以以无风险利率无限期地借入和贷出。在现实中，每个投资者都有信用额度。

• 所有证券都可以分成任意大小的部分。在现实中，通常不能购买或出售零股，并且某些资产有最低订单规模。

• 资产的风险/波动率是预先知道的/是恒定的。事实上，市场经常错误地定价风险（例如美国抵押贷款泡沫或欧洲债务危机），而波动率正在迅速变化。

更复杂的现代投资组合理论版本可以考虑更复杂的模型（例如具有非正态分布和税收的模型），但所有金融数学模型仍然依赖于许多不切实际的前提。

现代投资组合理论实际上并没有对市场进行建模

现代投资组合理论使用的风险、回报和相关性指标是基于期望值，这意味着它们是关于未来的数学陈述（回报的期望值在上述方程中是明确的，在方差和协方差的定义中是隐含的）。在实践中，投资者必须用基于资产回报和波动率历史测量的预测来替代这些方程中的值。这些期望值通常无法考虑到生成历史数据时不存在的新情况。

更重要的是，投资者被迫从过去的市场数据中估计关键参数，因为现代投资组合理论试图根据损失的可能性对风险进行建模，但没有说明这些损失可能发生的原因。使用的风险测量本质上是概率性的，而不是结构性的。这与许多工程风险管理方法相比是一个重大差异。

期权理论和现代投资组合理论至少与核电站进行的概率风险评估有一个重要的概念差异。PRA 是经济学家所说的结构模型。系统及其组件之间的关系在蒙特卡洛模拟中进行建模。如果阀门 X 发生故障，会导致泵 Y 的背压损失，导致流向容器 Z 的流量下降，等等。

但在布莱克-斯科尔斯方程和现代投资组合理论中，没有尝试解释价格变化的潜在结构。各种结果只是被赋予了概率。而且，与 PRA 不同，如果没有特定系统级事件（如流动性危机）的历史记录，就没有办法计算其发生的可能性。如果核工程师以这种方式进行风险管理，他们将永远无法计算特定工厂发生熔毁的可能性，除非在相同的反应堆设计中发生过几次类似的事件。

——道格拉斯·W·哈伯德，《风险管理的失败》，第 67 页，约翰·威利父子公司，2009 年。 ISBN 978-0-470-38795-5

本质上，现代投资组合理论的数学将市场视为一堆骰子。通过检查过去的市场数据，我们可以对骰子如何加权形成假设，但这对实际市场依赖于更大、更复杂、更混乱的系统（即世界）的情况没有帮助。因此，真实的金融市场的精确结构模型不太可能出现，因为它们本质上将是整个世界的结构模型。尽管如此，人们越来越认识到金融市场中系统性风险的概念，这应该会导致更复杂的市场模型。

数学风险测量也只有在它们反映了投资者真实担忧的程度上才有用——在实践中，对没有人关心的变量进行最小化毫无意义。现代投资组合理论使用方差的数学概念来量化风险，这在椭圆分布收益（例如正态分布收益）的假设下可能是合理的，但对于一般的收益分布，其他风险测量（如一致性风险测量）可能更好地反映投资者的真实偏好。

特别是，方差是一种对称度量，它将异常高的回报视为与异常低的回报一样危险。有些人会认为，在现实中，投资者只关心损失，并不关心高于平均回报的分散或紧密程度。根据这种观点，我们对风险的直观概念本质上是不对称的。

现代投资组合理论没有考虑投资决策的个人、环境、战略或社会维度。它只试图最大化风险调整后的回报，而不考虑其他后果。从狭义上讲，它完全依赖于资产价格，使其容易受到各种标准市场失灵的影响，例如由信息不对称、外部性和公共物品引起的市场失灵。它还奖励企业欺诈和不诚实的会计行为。从更广泛的意义上讲，公司可能具有影响其投资决策的战略或社会目标，而个人投资者可能具有个人目标。在这两种情况下，历史回报以外的信息都是相关的。

金融经济学家纳西姆·尼古拉斯·塔勒布也批评了现代投资组合理论，因为它假设了高斯分布

在股市崩盘（1987 年）之后，他们奖励了两个人物，哈里·马科维茨和威廉·夏普，他们基于高斯基础构建了美丽的柏拉图模型，并促成了所谓的现代投资组合理论。简单地说，如果你去除他们的高斯假设，并将价格视为可扩展的，那么你剩下的只是热空气。诺贝尔委员会本可以测试夏普和马科维茨模型——它们的作用就像互联网上出售的骗人疗法——但斯德哥尔摩似乎没有人考虑过这一点。

现代投资组合理论没有考虑其对资产价格的影响

多元化投资消除了非系统性风险，但代价是增加了系统性风险。多元化投资迫使投资组合经理在不分析基本面情况下投资资产，仅仅是为了消除投资组合的非系统性风险（CAPM假设投资所有可获得的资产）。这种人为增加的需求推高了资产价格，而这些资产在单独分析时，本身基本价值很低。其结果是，整个投资组合变得更加昂贵，因此，正回报的概率下降（即投资组合的风险增加）。

这方面的经验证据是，股票在被纳入标准普尔500等主要指数后通常会经历价格上涨。

扩展

自从MPT在1952年被提出后，人们做了很多尝试来改进该模型，特别是在采用更现实的假设方面。

后现代投资组合理论通过采用非正态分布的、不对称的风险度量来扩展MPT。这有助于解决其中一些问题，但不能解决其他问题。

Black-Litterman模型优化是对无约束Markowitz优化的扩展，它结合了对风险和回报的输入的相对和绝对“观点”。

其他应用

应用于项目组合和其他“非金融”资产

一些专家将MPT应用于除金融工具以外的项目组合和其他资产。当MPT应用于传统的金融投资组合之外时，必须考虑不同类型投资组合之间的一些差异。

1. 金融投资组合中的资产在实际应用中是连续可分的，而项目组合是“块状的”。例如，虽然我们可以计算出3支股票的最佳投资组合头寸分别是44%、35%、21%，但项目投资组合的最佳头寸可能不允许我们简单地改变在项目上的支出。项目可能是全有全无的，或者至少有不能分割的逻辑单位。投资组合优化方法必须考虑到项目的离散性。
2. 金融投资组合的资产是流动性的；它们可以随时评估或重新评估。但启动新项目的机会可能是有限的，并且可能出现在有限的时间窗口内。已经启动的项目不能在没有损失沉没成本的情况下放弃（即，半完成的项目几乎没有或根本没有回收/残值）。

这些情况并不能完全排除使用MPT和此类投资组合的可能性。它们仅仅表明需要使用一组额外的数学表达约束条件来运行优化，而这些约束条件通常不适用于金融投资组合。

此外，现代投资组合理论中一些最简单的要素适用于几乎任何类型的投资组合。通过记录投资者在特定回报下可接受的风险程度来捕捉投资者风险偏好的概念，可以应用于各种决策分析问题。MPT使用历史方差作为风险度量，但像重大项目这样的资产投资组合没有明确的“历史方差”。在这种情况下，MPT投资边界可以用更通用的术语表达，例如“回报率低于资本成本的可能性”或“损失超过投资金额一半的可能性”。当将风险表述为对预测和可能损失的不确定性时，该概念就可以转移到各种类型的投资中。

应用于其他学科

在20世纪70年代，现代投资组合理论中的概念被引入区域科学领域。在一系列开创性的著作中，迈克尔·康罗伊使用投资组合理论方法对经济中的劳动力进行了建模，以考察劳动力的增长和波动性。之后，出现了大量关于经济增长与波动性之间关系的文献。

最近，现代投资组合理论被用来对社会心理学中的自我概念进行建模。当构成自我概念的自我属性构成一个多元化的投资组合时，个体层面的心理结果，如情绪和自尊，应该比自我概念不多元化时更稳定。这一预测已在涉及人类受试者的研究中得到证实。

近年来，现代投资组合理论被应用于信息检索中对文档之间不确定性和相关性的建模。给定一个查询，目标是最大化排名列表中文档的整体相关性，同时最小化排名列表的整体不确定性。

与套利定价理论比较

SML和CAPM通常与套利定价理论（APT）形成对比，后者认为，金融资产的预期回报可以建模为各种宏观经济因素的线性函数，其中对每个因素变化的敏感性由特定因素的贝塔系数表示。

APT在其假设方面不太严格：它允许资产回报的统计模型，并假设每个投资者将持有具有自己独特贝塔数组的独特投资组合，而不是相同的“市场投资组合”。然而，与CAPM不同的是，APT本身并没有揭示其定价因素的身份——这些因素的数量和性质可能会随着时间和经济体的变化而变化。

进一步阅读

• Lintner，John (1965)。“风险资产的估值以及股票投资组合和资本预算中风险投资的选择”。《经济学与统计学评论》。麻省理工学院出版社。47 (1): 13–39。 doi:10.2307/1924119。 JSTOR 1924119. {{cite journal}}: 引用具有空的未知参数：|month= 和 |coauthors= (帮助)
• Sharpe，William F. (1964)。“资本资产价格：风险条件下市场均衡理论”。《金融杂志》。19 (3): 425–442。 doi:10.2307/2977928。 JSTOR 2977928. {{cite journal}}: 引用具有空的未知参数：|month= 和 |coauthors= (帮助)
• Tobin, James (1958). "流动性偏好作为对风险的态度". 经济研究评论. 25 (2): 65–86. doi:10.2307/2296205. JSTOR 2296205. {{cite journal}}: 引用包含空白未知参数：|coauthors= 和 |month= (帮助)

外部链接

• 免费股票投资组合优化在线 允许用户比较股票表现，进行免费股票分析，以及优化股票投资组合。
• 宏观投资分析, 威廉·F·夏普教授，斯坦福大学
• 投资理论导论

, 威廉·N·戈茨曼教授，耶鲁管理学院