谜题/哥尼斯堡七桥
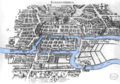
在18世纪早期,有一座名为哥尼斯堡(现称为加里宁格勒)的城市,它曾是普鲁士的一个古老城市(以前是德国的一个飞地,现在属于俄罗斯),位于普雷戈利亚河畔。这座城市的布局本身就很独特,因为克奈普霍夫岛(现在称为康德岛)被包围,有两个中心陆地由7座桥连接(参见图1),在古代,如图所示。
据说,这七座桥分别称为铁匠桥、连接桥、绿桥、商人桥、木桥、高桥和蜂蜜桥。
哥尼斯堡的市民过去常常在星期天下午在他们美丽的城市里散步。在散步的时候,市民们决定为自己创造一个游戏,他们的目标是设计一种方法,让他们可以绕着城市散步,只穿过这七座桥一次,并且只走一次。尽管哥尼斯堡的市民中没有人能设计出一条路线让他们只穿过每座桥一次,但他们仍然无法证明这是不可能的。
不幸的是,在哥尼斯堡,事情并没有那么顺利。普鲁士解体后,哥尼斯堡最终成为俄罗斯的一部分(自那以后,这座城市被改名为加里宁格勒)。二战期间,盟军在1942年炸毁了两座原始的桥,并在战后重建。后来又拆除了另外两座桥,为高速公路让路。现在,在21世纪,人们可以利用剩下的五座桥,在一次散步中完成绕城市的旅程。
莱昂哈德·欧拉(参见图2),一位瑞士数学家,对这个问题很感兴趣,当时,几何、代数甚至计数的艺术都不足以解决它。
1735年8月,欧拉发表了一篇题为“Solutio problematis ad geometriam situs pertinentis”的论文。
在这篇论文的第一段中,欧拉指出,他认为这个问题与几何有关,但并非他同时代人所熟知的测量和计算的几何,而是他称之为位置几何的一种新型几何。
他指出,每个陆地内部的路线选择并不重要。路线的唯一重要属性是穿越桥梁的顺序。因此,他将问题抽象化了。欧拉提供了这个问题的草图,并删除了地图的所有特征,除了陆地的清单(他用A、B、C、D标记)和连接它们的桥梁(a、b、c、d、e、f、g)。(参见图3)他提出了这个问题的一般问题,“能否确定是否可以正好穿过每座桥一次?”
在第三段中,欧拉告诉读者,为了解决这个问题,他可以写下所有可能的路径,但这种方法将花费大量时间,而且对于具有更多桥梁和陆地的更大的配置,这种方法将不起作用。由于这些问题,欧拉决定选择另一种方法来解决这个问题。
在第四段和第五段中,欧拉开始简化问题,用抽象的“顶点”或节点代替每个陆地。然后,他用抽象的连接,即“边”来代替每座桥。边(道路)记录了哪些顶点(陆地)是连接的。这样,他就形成了一个图。每个交叉点将被标记如下:如果交叉点从陆地A到陆地B,它将被称为AB。(参见图4)
在第五段中,欧拉继续讨论这个过程,解释说在ABDC中,尽管有四个大写字母,但只穿过了三座桥。欧拉解释说,无论有多少桥,都会多一个字母来表示必要的穿越。因此,哥尼斯堡七桥问题需要穿越七座桥,因此实际上,需要八座桥才能穿越。
总而言之,欧拉指出,“一般来说,如果桥梁的数量是任何奇数,并且增加1,那么A出现的次数就是结果的一半。”这意味着,每座桥都有两个端点,每个桥的端点都位于其他陆地。因此,桥梁端点的数量等于桥梁数量的两倍,并且始终是一个偶数。当我们在一个区域中计算桥梁连接的数量时,我们是在计算桥梁的端点。因此,如果某个区域有奇数个连接,那么肯定还有另一个区域有奇数个连接,因为所有桥梁端点的总和必须是偶数。
-
图1:带有河流和桥梁的旧哥尼斯堡地图,颜色标注
-
图2:莱昂哈德·欧拉的肖像
-
图3:莱昂哈德·欧拉关于哥尼斯堡桥的草图
-
图4:哥尼斯堡七桥的简化