拼图/符号

符号型网格拼图之所以这样命名，是因为它主要需要符号（数字、字母或有时是符号）来填充单元格以解决网格拼图。最流行的之一是数独。

数独

规则

• 在每一行、每一列和 3X3 方格中，将 1 到 9 恰好放置一次。

• 
  已解决数独的示例

像ABC一样简单

规则

• 在网格内的每个单元格的行和列中，将字母 A、B 和 C 各放置一次。
• 因此，在 5X5 网格中，每列和每行的至少 2 个单元格将为空。
• 网格外部的字母表示在该行的末端和该列的末端，哪个字母最接近该末端。

• 
  空的拼图
• 
  已解决的拼图

数独

规则

• 对于每一行和每一列，将放置数字 1-5（不重复），它们将遵循不等号。
• 某些单元格之间的大于“>”符号表示一个单元格的值始终大于另一个单元格的值，如符号所示。该符号始终指向较小的数字。

• 
  已解决数独的示例

肯肯 / 数独计算

规则

• 将数字 1 到 6 分别放置到网格的每一行和每一列中，同时遵守区域总和。
• 每个区域的左上角的值必须在该区域中的所有数字之间应用给定运算（+，-，/，*）后获得。对于 - 和 /，运算从区域中的最大数字开始，然后以任意顺序减去或除以其他数字。

• 
  已解决肯肯/数独计算的示例

数独加

规则

• 在每个白色单元格中放置数字 1 到 9。
• 在任何一组中，不能重复使用一个数字。
• 每条水平组的总和出现在组左侧的对角线上。
• 每条垂直组的总和出现在组上方的对角线上。

• 
  数独加的示例

国王之旅

规则

• 填充空单元格，使每个单元格恰好包含一次数字 1 到 64。
• 从数字 1 开始，使用的路线必须以左、右、上、下或对角线的方式访问每个网格一次，从而使每个网格单元格恰好访问一次。

摩天大楼

规则

• 将数字 1 到 5 放置到网格的每一列和每一行中。网格的放置方式使得外部的提示数字表示从该点可以“看到”的数字数量。
• 如果一个数字前面没有更高的数字，则该数字是可见的，沿着该行或该列按顺序读取。参见《摩天大楼中的视线解释》以了解更多说明。

在上例中，我们只能看到 2 个方块，即第 4 层（第 3 层被它遮挡）和第 5 层高度（第 1 层和第 2 层被它遮挡）。

在下例中，我们只能看到 2 个方块，即第 2 层（第 1 层被它遮挡）和第 5 层高度（第 3 层和第 4 层被它遮挡）。

• 
  空的拼图
• 
  已解决的拼图
• 
  摩天大楼拼图中的视线解释

涟漪效应

规则

• 在每个区域中放置一个数字，使得每个粗线区域都具有每个数字（这相当于该区域中的单元格总数）。
• 一行或一列中的相等数字必须至少间隔由该数字指定的单元格数量。

• 
  空的涟漪效应拼图
• 
  已解决的涟漪效应拼图

二进制

规则

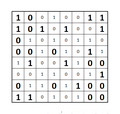
• 在每一列和每一行中放置 1 和 0，使得每一行和每一列都有相同数量的 0 和 1。
• 沿着列或行，连续的 0 或 1 的数量不应超过两倍。

• 
  一个空的二进制拼图
• 
  已解决的二进制拼图

拼图字母

规则

• 在每行、每列和粗线区域中，将 A 到 E 分别放置一次

• 
  拼图空白
• 
  拼图完成

没有连续 4 个

规则

• 在每个空单元格中放置“X”或“O”，以确保垂直、水平或对角线上没有四个（4）个连续的“X”或“O”。

• 
  没有连续 4 个拼图空白
• 
  没有连续 4 个拼图完成