标量是数字,或表示数字的量,例如 
向量由方向和大小组成,或多个标量分量组成,例如  向量的模可以通过勾股定理求得,
向量的模可以通过勾股定理求得, 
当向量乘以标量时,向量的每个分量都乘以标量,例如 
 角度
角度  、向量
、向量  和
和  之间关系的描述,以及点积
之间关系的描述,以及点积 
两个向量的点积(或标量积)由 给出。点积等于向量之间夹角的余弦乘以它们模长的乘积,因此向量之间的夹角可以使用
给出。点积等于向量之间夹角的余弦乘以它们模长的乘积,因此向量之间的夹角可以使用 轻松计算。
轻松计算。
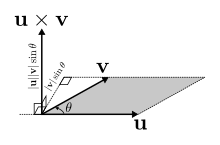 向量
向量 和
和 的叉积的描述。
的叉积的描述。
两个向量的叉积得到另一个向量,它垂直于这两个初始向量。叉积的大小等于这两个向量形成的平行四边形的面积,或 。
。


 、向量
、向量  和
和  之间关系的描述,以及点积
之间关系的描述,以及点积 



 和
和 的叉积的描述。
的叉积的描述。