半导体/掺杂

半导体

在检查晶体时，我们为了简便起见，对它们做了一些假设，例如

虽然无限的说法有点模糊，但这是一个相当好的近似，因为这些晶体通常比晶体内部的距离大得多。

由于晶体存在于3D空间中并且是周期性的，如果我们在其中一个轴上移动晶体的大小，我们将处于一个对应的位置。在数学上，我们说我们有三个线性无关的向量，并且可以移动它们的整数值到晶格中的对应位置。

$\mathbf {r} =u\mathbf {a} +v\mathbf {b} +w\mathbf {c}$

晶胞

如果我们有一个晶格，它一定是由更小的组件组成的，晶胞是晶格中最小的不可分割的部分。通过将许多晶胞放在一起，您可以再次创建整个晶格。想象一堆骰子，你可以说一个骰子是这个晶体晶格的晶胞。

存在无限数量的可能的晶胞，但只有 14 种类型的晶格。这可以推广到 7 个晶体类。

此外，晶胞存在最小尺寸，其体积为 1 个晶格点（原子/分子/任何东西）。

想象一个立方晶胞，每个角都有一个点。所以总共有 8 个点，但这些点中的每一个都与它和其他 7 个立方体共享。

所以每个晶胞的晶格点数为 8 * 1/8 = 1。我们称之为原胞。

现在，如果我们将每个点想象成一个与相邻点接触的球体，那么我们可以将填充率定义为点所占体积与晶胞体积的比率。

在立方晶胞中，每个球体的半径将是晶体大小的一半。所以我们说 r = a/2。

V_{point}={\frac {4}{3}}\pi r^{3}={\frac {4}{3}}\pi \left({\frac {a}{2}}\right)^{3}

并且每个晶胞中只有一个，即原胞 = 1。所以

PackingFraction={\frac {V_{point}}{V_{cell}}}={\frac {{\frac {4}{3}}\pi \left({\frac {a}{2}}\right)^{3}}{a^{3}}}={\frac {\pi }{6}}

或 52%

就像一个立方晶胞，除了在它的中心还有一个晶格点。

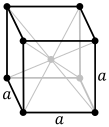
原胞 = 8 * 1/8 + 1 = 2。

它的填充率为 68%。

这是一个密堆积晶格，它就像一个立方体，只是所有 6 个面都在它们的中心有另一个点。

原胞 = 8 * 1/8 + 6 * 1/2 = 4

填充率 = 74%