半导体/PN结

简单模型

这些简单模型是对相当通用的二极管工作原理的小信号近似。齐纳二极管和隧道二极管被忽略。

在第一近似中，二极管是一种允许电流在一个方向上以零电阻流动，并在另一个方向上以无限电阻阻断电流的器件。基本上，它像电流的单向阀。

第二个近似包括正向电流流动时恒定的压降。压降随二极管类型而变化，但对于相当通用的二极管通常约为 0.7 伏，对于 LED 则超过 1 伏。

为了获得第三个近似，在二极管中添加一点电阻。现在事情变得稍微复杂了一些。由于 v-i 曲线是非线性的，因此电阻不是恒定的。但是，如果你的信号很小并且在一个较大的偏移量上承载，你可以通过正确选择压降和电阻来进行相当准确的分析。

最后，第四个近似考虑了二极管反向偏置时存在的小泄漏电流。对于大多数通用二极管，这通常在纳安培到几微安培的范围内。

如果你需要比这更高的精度，你需要查看二极管内部发生的物理现象。

二极管物理分析

二极管结可以用 N 型和 P 型半导体或半导体和金属结形成。

as $\Phi$.

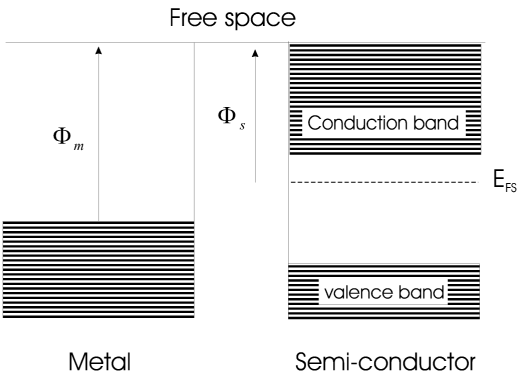金属和半导体的费米能级图。

当金属和半导体接触在一起时，多余的电子从半导体扩散到金属，直到费米能级相等。当电子从半导体扩散到金属时，它们会留下它们的施主原子。这会使界面附近的区域耗尽载流子，因此该区域的导电性不佳。因此，为了使电荷扩散穿过该区域，它们需要额外的能量。由于电荷耗尽的程度是距离的某个函数，因此导带弯曲以表示该区域扩散所需的能量。

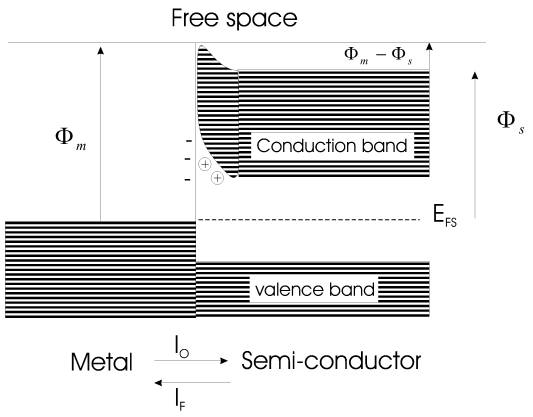金属和半导体的费米能级图。

现在将存在两种电流。电子在耗尽区产生的势垒上从金属扩散到半导体 $I_{O}$。电子从半导体在相反方向上跨越该势垒扩散 $I_{F}$。当没有施加外部电压时，电流将相等且相反。

如果电子具有足够的能量克服势垒，它们将从半导体扩散到金属。电子的能量是统计性的，由麦克斯韦-玻尔兹曼分布[1]给出。因此，随着温度升高，占据较高能量状态的电子数量增加的概率也会增加。对于低掺杂浓度，也可以应用麦克斯韦-玻尔兹曼分布。但是，对于非零温度，大多数来自掺杂剂的多余电子将存在于导带中。

麦克斯韦-玻尔兹曼分布指出：给定能量 W，能量大于 W 的电子数量由下式给出

$n_{W}=n\cdot e^{\frac {-W}{kT}}$

其中 n 是电子数密度，k 是玻尔兹曼常数，T 是温度。

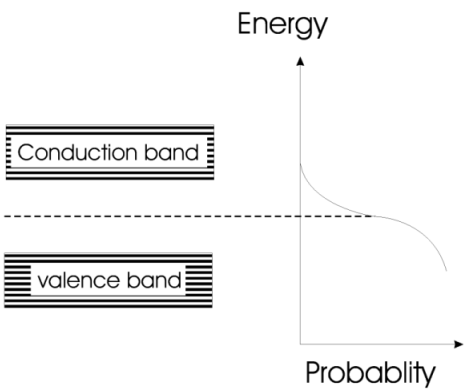费米能级附近电子的概率密度函数

麦克斯韦-玻尔兹曼分布不适用于金属。原因可以在参考文献[1]中找到。对于小电压，可以假设 $I_{O}$ 为常数。

$I_{F}=nqe^{\frac {-q\Psi }{kT}}$

$I_{O}=I_{F}$ 对于没有外部电势。这种平衡存在于我们将称为 $\Psi$ 的扩散势中，其中 $\Psi =\phi _{m}-\phi _{s}$。因此，电子跨越该势垒的能量由 $q\Psi$ 给出。

$I_{O}=I_{F}=nq\cdot e^{\frac {-q\Psi }{kT}}$

$nq=I_{O}\cdot e^{\frac {q\Psi }{kT}}$

N型半导体的费米能级可以通过外部电势升高。这将增加电子跨越势垒扩散的能量。因此，电子跨越势垒所需的能量将变为$q(\Psi -V)$.

$I_{F}=nq\cdot e^{\frac {-q(\Psi -V)}{kT}}$

$I_{F}=I_{O}\cdot e^{\frac {q\Psi }{kT}}\cdot e^{\frac {-q(\Psi -V)}{kT}}$

$I_{F}=I_{O}\cdot e^{\frac {qV}{kT}}$

因此

$I_{D}=I_{F}-I_{O}$

令

$V_{T}={\frac {kT}{q}}$

那么

$I_{D}=I_{O}{\bigg (}e^{\frac {V_{D}}{V_{T}}}{\bigg )}-I_{O}$

$I_{D}=I_{O}{\bigg (}e^{\frac {V_{D}}{V_{T}}}-1{\bigg )}$

耗尽宽度

耗尽宽度由实现扩散势所需的电荷量决定。因此，如果知道材料的掺杂密度和相对介电常数，就可以计算出耗尽宽度。

二极管结的耗尽区

耗尽宽度最容易通过泊松方程 [1] 实现。假设掺杂密度恒定。

根据泊松方程

${\frac {\partial ^{2}}{\partial x^{2}}}V(x)={\frac {\rho }{\varepsilon }}$

其中 $\rho =qN_{d}$ 为电荷密度，$\varepsilon$ 为介电常数，x 为距离结的距离。

$V={\frac {qN_{d}x^{2}}{2\varepsilon _{0}\varepsilon _{r}}}$

耗尽宽度是势垒高度的某个函数，$(\Psi -V)$。因此求解$x=W_{d}$

$\Psi -V={\frac {qN_{d}W_{d}^{2}}{2\varepsilon _{0}\varepsilon _{r}}}$

$W_{d}={\sqrt {\frac {2\varepsilon _{0}\varepsilon _{r}(\Psi -V)}{qN_{d}}}}$

耗尽电容

电容是指在耗尽区宽度变化时，电荷变化量与电压变化量的比值。

已知

$C={\frac {\partial Q}{\partial V}}$

$Q=qN_{d}W_{d}YZ$

那么

$C={\frac {\partial (qN_{d}W_{d}YZ)}{\partial (\Psi -V)}}$

$C=qN_{d}YZ{\frac {\partial W_{d}}{\partial (\Psi -V)}}$

$C=qN_{d}YZ\cdot {\frac {2\varepsilon _{0}\varepsilon _{r}}{qN_{d}}}\cdot -{\frac {1}{2}}{\bigg (}{\frac {2\varepsilon _{0}\varepsilon _{r}(\Psi -V)}{qN_{d}}}{\bigg )}^{-{\frac {1}{2}}}$

$C=-{\frac {1}{2}}qN_{d}YZ\cdot {\sqrt {\frac {2\varepsilon _{0}\varepsilon _{r}}{qN_{d}}}}{\sqrt {\frac {2\varepsilon _{0}\varepsilon _{r}}{qN_{d}}}}\cdot {\sqrt {\frac {qN_{d}}{2\varepsilon _{0}\varepsilon _{r}(\Psi -V)}}}\cdot {\frac {\sqrt {\Psi }}{\sqrt {\Psi }}}$

$C=-{\frac {1}{2}}qN_{d}YZ\cdot {\sqrt {\frac {2\varepsilon _{0}\varepsilon _{r}}{qN_{d}}}}\cdot {\frac {1}{\sqrt {\Psi }}}\cdot {\sqrt {\frac {\Psi }{\Psi -V}}}$

$C=-{\frac {1}{2}}qN_{d}YZ\cdot {\sqrt {\frac {2\varepsilon _{0}\varepsilon _{r}}{qN_{d}\Psi }}}\cdot {\frac {1}{\sqrt {1-V/\Psi }}}$

令

$C_{0}=-{\frac {1}{2}}qN_{d}YZ\cdot {\sqrt {\frac {2\varepsilon _{0}\varepsilon _{r}}{qN_{d}\Psi }}}$

因此

$C={\frac {C_{0}}{\sqrt {1-V/\Psi }}}$

参考文献

[1] John Allison. Electronic Engineering Semiconductors and devices. McGraw-Hill Book Company, Shoppenhangers Rd Maidenhead Berkshire England,1971.