信号与系统/频率响应

频率响应

系统对不同频率的输入信号有不同的响应。某些系统可能放大某些频率的成分，而衰减其他频率的成分。系统输出与系统输入在不同频率上的关系被称为系统的频率响应。

频率响应是系统输入和输出在傅立叶域的关系。

在这个系统中，X(jω) 是系统输入，Y(jω) 是系统输出，H(jω) 是频率响应。我们可以定义这些函数之间的关系为

$Y(j\omega )=H(j\omega )X(j\omega )$

${\frac {Y(j\omega )}{X(j\omega )}}=H(j\omega )$

频率响应函数

由于频率响应是一个复数函数，我们可以将其转换为复平面上的极坐标形式。这将给我们一个幅值和一个角度。我们将这个角度称为相位。

幅频响应

对于每个频率，幅值表示系统放大或衰减输入信号的趋势。

$A\left(\omega \right)=\left|{H\left({j\omega }\right)}\right|$

相频响应

相位表示系统改变输入正弦信号相位的趋势。

$\phi \left(\omega \right)=\angle H\left({j\omega }\right)$.

相频响应，或其导数群延迟，告诉我们系统如何延迟输入信号作为频率的函数。

例子

例子：电路

考虑以下具有相量输入和输出电压的通用电路

其中

$V_{o}\left({j\omega }\right)=V_{om}\cos \left({\omega t+\theta _{o}}\right)=V_{om}\angle \theta _{o}$

$V_{i}\left({j\omega }\right)=V_{im}\cos \left({\omega t+\theta _{i}}\right)=V_{im}\angle \theta _{i}$

和之前一样，我们可以将这个电路的系统函数H(jω)定义为

$H\left({j\omega }\right)={{V_{o}\left({j\omega }\right)} \over {V_{i}\left({j\omega }\right)}}$

$A\left(\omega \right)=\left|{H\left({j\omega }\right)}\right|={{\left|{V_{o}\left({j\omega }\right)}\right|} \over {\left|{V_{i}\left({j\omega }\right)}\right|}}={{V_{om}} \over {V_{im}}}$

$\phi \left(\omega \right)=\angle H\left({j\omega }\right)=\angle \left({{V_{o}\left({j\omega }\right)} \over {V_{i}\left({j\omega }\right)}}\right)=\angle V_{o}\left({j\omega }\right)-\angle V_{i}\left({j\omega }\right)=\theta _{o}-\theta _{i}$

重新排列得到以下转换

$V_{om}=A\left(\omega \right)V_{im}$

$\theta _{o}=\theta _{i}+\phi \left(\omega \right)$

示例：低通滤波器

我们将使用一个简单的低通滤波器作为示例来说明这种方法。这种类型的电路允许低频通过，但阻止高频。

求解以下 RC 电路的频率响应函数，进而求解幅度和相位响应函数（已处于相量形式）。

首先，我们使用分压器规则根据输入相量得到输出相量。

$V_{o}\left({j\omega }\right)=V_{i}\left({j\omega }\right)\cdot {{1 \over {j\omega C}} \over {R+{1 \over {j\omega C}}}}$

现在我们可以很容易地确定频率响应。

$H\left({j\omega }\right)={{V_{o}\left({j\omega }\right)} \over {V_{i}\left({j\omega }\right)}}={{1 \over {j\omega C}} \over {R+{1 \over {j\omega C}}}}$

简化后得到：

$H\left({j\omega }\right)={1 \over {1+j\omega RC}}$

由此我们可以得到幅度和相位响应

$A\left(\omega \right)=\left|{H\left({j\omega }\right)}\right|={1 \over {\sqrt {1+\left({\omega CR}\right)^{2}}}}$

$\phi \left(\omega \right)=\angle H\left({j\omega }\right)=\tan ^{-1}\left({0 \over 1}\right)-\tan ^{-1}\left({{\omega RC} \over 1}\right)=-\tan ^{-1}\left({\omega RC}\right)$

频率响应由幅度和相位响应的图形表示

当这些图形在适当的对数刻度上绘制时，通常更容易解释

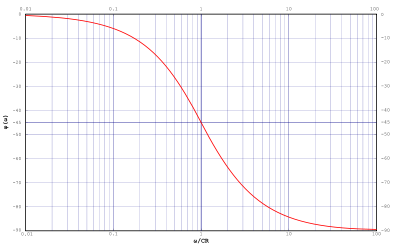
这表明该电路确实是一个滤除较高频率的滤波器。这种滤波器被称为低通滤波器。

可以使用称为频谱分析仪或增益和相位测试仪的仪器绘制任意电路的幅度和相位响应。有关使用这些仪器的更多详细信息，请参见实用电子学。

滤波器

从这些示例中可以得出的一个重要概念是，通过设计一个称为滤波器的适当系统，我们可以选择性地衰减或放大某些频率范围。这意味着我们可以最小化某些不希望的频率成分（例如噪声或竞争数据信号），并最大化我们自己的数据信号

我们可以将“接收信号”r定义为数据信号d和不希望的成分v的组合

$r(t)=d(t)+v(t)$

我们可以取r的能量谱密度来确定数据信号d的频率范围。我们可以设计一个试图放大这些频率范围并衰减v的频率范围的滤波器。我们将在接下来的几章中讨论这个问题和滤波器的一般问题。有关此主题的更深入讨论，请参阅信号处理书籍。