时域中的声音

声波的出现和行为

声音的度量（声学）定义是压力波和密度的变化，这是由波在介质中的传播引起的。在约 25Hz 到 18kHz 之间，人类的听觉系统会感知到这些波，因为它们会导致耳鼓运动。这种机械运动在耳蜗中被转化为神经冲动，并被发送到大脑的听觉区域进行分析。声波是随着时间的推移而变化的气压，可以用随着时间的推移而变化的电压或数据流来表示。这是一种声音的“时间/幅度”表示，也称为幅度时间线。幅度表示气压变化引起的分子位移。在数字域中，幅度通常表示为1到-1之间的值，其中1和-1表示信号的最大正值和负值幅度，而0表示零幅度。

图 1.1中的波形称为正弦波或正弦。正弦波可以被认为是声音的基本组成部分。该图表明幅度随时间变化，但这种变化模式周期性地重复。

图 1.2中的波形比1.1中的正弦波更复杂。存在不同幅度的峰值和谷值，并且尽管模式随着时间的推移而重复（看看你是否能找到它），但它更难发现。正如正弦波以简单的方式表现并听起来简单一样，这种声音以更大的复杂性表现并也听起来更复杂。因此，随时间变化的详细、复杂的声音在如此近距离查看时往往没有可辨别的特征——可能没有重复的模式或行为，我们可以用它来告诉我们关于声音的信息。

在图 1.3中，我们看到了一种声音在约 2 秒而不是 2 毫秒内的外观。从这个角度来看，我们可以看到整体声音幅度随时间的变化方式；特别地，高幅度部分可以很容易地被视为鼓声——它们突然出现并且迅速降低幅度，正如人们对敲击鼓面所期望的那样。如果这种声音是在几毫秒的范围内观察到的，那么可能很难判断是哪种乐器在演奏。由此，我们应该得出结论，短时间间隔和长时间间隔的视角都显示了不同类型的信息，并且选择适合自己需求的正确视角非常重要。

正弦波、频率和音高

如图 1.1所示，正弦波具有周期性形式，每 $T\,$ 秒重复一次，称为周期，循环。该波还具有正最大幅度， $A\,$ ，以及负最大幅度， $-A\,$ 。正弦波的频率， $f\,$ ，是每秒的循环次数，以赫兹（Hz）为单位测量。我们可以从以下公式中获得频率从波长

f={\frac {1}{T}}\,

此外，我们可以用以下数学形式来表示正弦波（角度以弧度表示）。这种形式可能对有兴趣在代码中创建自己的可控正弦函数的程序员有用

p(t)=Asin\left({\frac {2\pi t}{T}}\right)=Asin(2\pi ft)

从心理测量学来看，较高的频率（例如高于 1.5kHz）通常与“明亮”等词语相关联，而较低的频率（例如低于 200Hz）通常与“深度”或“低音”等词语相关联。中间范围可能与“温暖”一词相关联。例如，一种乐器，如以干净的方式演奏的电吉他，可能会被称为“明亮”或“尖锐”，而一把低音提琴可能会被称为“暗淡”和“温暖”。由于是心理测量学，这些术语不是我们可以精确测量的客观量，而是经常用来描述特定声音的音色或音调颜色。声音中存在的不同频率的各种幅度，以及它们随着时间的推移而演变是与音色相关的主要因素，并且可以通过组成声音的不同频率的组合来实现无限的音色。在心理测量学方面，人类听觉将整数频率比与音高相关联，并将特定频率与标准西方音阶中的特定音符相关联

波长 (t)	频率 (Hz)	音符名称
156.82 厘米	220.0	A3
139.71 厘米	246.94	B3
131.87 厘米	261.63	C4
117.48 厘米	293.66	D4
104.66 厘米	329.63	E4
98.79 厘米	349.23	F4
88.01 厘米	392.0	G4
78.41 厘米	440.0	A4

图 1.4。波长、频率和音符名称之间的关系。

请注意，此表涵盖了八度的范围。频率加倍，波长减半。

正弦波的构造和解构

利用傅里叶分析，正弦波可以被认为是声音的基本组成部分，因为单个正弦波是单个频率。在傅里叶分析中，结合不同频率、幅度和相位的正弦波可以重建任何声音的频谱。类似地，复杂的声音可以根据频率、幅度和相位进行分析。

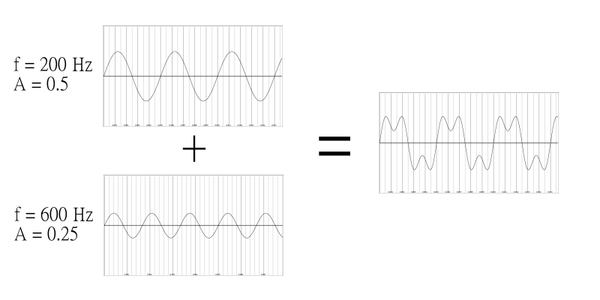
图 1.5展示了两个正弦波加在一起的外观。两个波的特性在结果波形中结合在一起。这种技术是加法合成的基础，这将在本书的后面部分讨论。此外，在声音的构建方式中，可以从整体中滤除两个组成频率；这通常通过在频域中分析波形来完成，这将在下一章中讨论。