狭义相对论/动力学

介绍

由于相对论理论，粒子速度在相对运动的观察者之间存在差异的方式意味着动量需要重新定义。

下图显示了两个粒子的典型碰撞。在右手系中，碰撞是从与其中一个粒子以相同速度运动的观察者的角度观察的，在左手系中，它是从以介于两个粒子速度之间的速度运动的观察者的角度观察的。

如果重新定义动量，那么所有变量（如力（动量变化率）、能量等）都将被重新定义，相对论将导致完全新的物理学。新物理学通过关系 $K=\gamma mc^{2}-mc^{2}\,$ 对普通体验产生影响，因此它是伽马与1之间的微小偏差，以日常动能的形式表达出来，因此整个物理学都与“相对论”推理有关，而不是牛顿的经验观点。

动量

在物理学中，动量在一个封闭的系统中是守恒的，动量守恒定律适用。考虑以下所示的相同粒子对称碰撞的特例

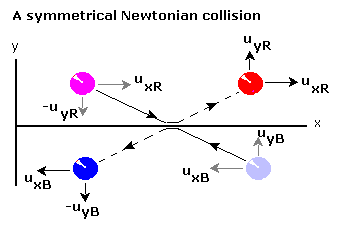
红色球的动量变化是

$2m\mathbf {u_{yR}}$

蓝色球的动量变化是

$-2m\mathbf {u_{yB}}$

情况是对称的，因此证明了牛顿动量守恒定律

$2m\mathbf {u_{yR}} =2m\mathbf {u_{yB}}$

请注意，此结果取决于速度的 y 分量相等，即 $\mathbf {u_{yR}} =\mathbf {u_{yB}}$.

相对论情况则大不相同。碰撞如下图所示，左手系显示了碰撞在一位观察者看来是什么样子，而右手系显示了完全相同的碰撞在与蓝色球以相同速度运动的另一位观察者看来是什么样子

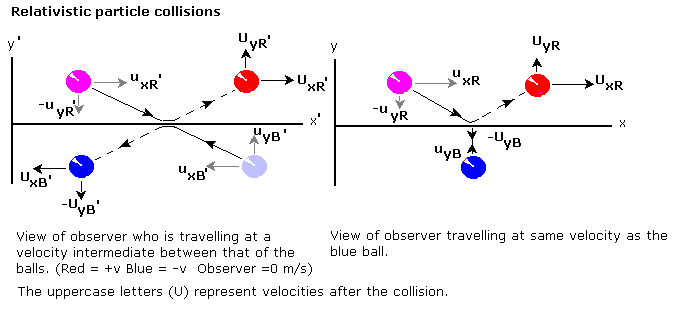
上面所示的配置已简化，因为一个系包含一个静止的蓝色球（即：$u_{xB}=0$）并且速度的选择使得红色球的垂直速度在碰撞后正好反转，即：$u_{yR}^{'}=u_{yB}^{'}$。这两个系都显示了完全相同的事件，只有观察者在不同的系之间有所不同。系之间的相对论速度变换是

$u_{yR}^{'}={\frac {u_{yR}{\sqrt {1-v^{2}/c^{2}}}}{1-u_{xR}v/c^{2}}}$

$u_{yB}^{'}={\frac {u_{yB}{\sqrt {1-v^{2}/c^{2}}}}{1-u_{xB}v/c^{2}}}=u_{yB}{\sqrt {1-v^{2}/c^{2}}}$ 给定$u_{xB}=0\,$.

假设在某个参考系中 y 分量相等，在牛顿物理学中，它们在另一个参考系中也将相等。然而，在相对论中，如果在某个参考系中 y 分量相等，它们在另一个参考系中不一定相等（时间膨胀不是方向性的，因此垂直速度在观察者之间不同）。例如，如果$u_{yR}^{'}=u_{yB}^{'}$，则

$u_{yB}={\frac {u_{yR}}{1-u_{xR}v/c^{2}}}$

因此，如果$u_{yR}^{'}=u_{yB}^{'}$，那么在这种情况下$u_{yR}\neq u_{yB}$.

如果在碰撞之间和参考系之间质量是恒定的，那么尽管$2mu_{yR}^{'}=2mu_{yB}^{'}$，人们发现

$2mu_{yR}\neq 2mu_{yB}$

因此，定义为质量乘以速度的动量在碰撞中不守恒，当碰撞在彼此相对运动的参考系中描述时。请注意，如果$u_{xR}$和$v$很小，这种差异非常小。

为了在所有惯性参考系中保持动量守恒原理，动量的定义必须改变。新的定义必须在物体以远小于光速的速度运动时简化为牛顿表达式，以便恢复牛顿公式。

当观察者以与蓝色球体相同的速度运动时，即当$u_{xB}=0\,$时，y 方向上的速度由以下方程关联：

$u_{yB}={\frac {u_{yR}}{1-u_{xR}v/c^{2}}}$

如果我们将蓝球的质量记为 $m_{B}$，红球的质量记为 $m_{R}$（从蓝球的参考系观察），那么如果相对论原理成立

$2m_{R}u_{yR}=2m_{B}u_{yB}\,$

所以

$m_{R}=m_{B}{\frac {u_{yB}}{u_{yR}}}$

但是

$u_{yB}={\frac {u_{yR}}{1-u_{xR}v/c^{2}}}$

因此

$m_{R}={\frac {m_{B}}{1-u_{xR}v/c^{2}}}$

这意味着，如果相对论原理要成立，那么为了使动量守恒定律成立，质量必须按上述方程所示的量变化。

粒子速度的选择使得 $u_{yR}^{'}=u_{yB}^{'}$。 $v$ 的选择使得 $v=u_{xR}^{'}$。 这允许 $v$ 用 $u_{xR}\,$ 表示

$u_{xR}^{'}={\frac {u_{xR}-v}{1-u_{xR}v/c^{2}}}=v$

因此

$v={\frac {c^{2}}{u_{xR}}}(1-{\sqrt {1-u_{xR}^{2}/c^{2}}})$

所以将 $v$ 代入 $m_{R}={\frac {m_{B}}{1-u_{xR}v/c^{2}}}$

$m_{R}={\frac {m_{B}}{\sqrt {1-u_{xR}^{2}/c^{2}}}}$

蓝色球体处于静止状态，因此它的质量有时被称为它的静止质量，并用符号 $m$ 表示。由于球体在加速开始时是相同的，红色球体的质量是一个蓝色球体相对于观察者运动时的质量；这个质量有时被称为相对论质量，用符号 $M$ 表示。这些术语现在很少在现代物理学中使用，将在本节末尾解释。上述讨论与蓝色球体和红色球体的相对运动有关，因此 $u_{xR}$ 对应于相对于蓝色球体静止的观察者而言的运动球体的速度。这些考虑意味着相对论质量由下式给出：

$M={\frac {m}{\sqrt {1-u^{2}/c^{2}}}}$

相对论动量由相对论质量和速度的乘积给出 $\mathbf {p} =M\mathbf {u}$.

动量相对于静止质量的整体表达式为：

$\mathbf {p} ={\frac {m\mathbf {u} }{\sqrt {1-u^{2}/c^{2}}}}$

动量的分量为：

$p_{x}={\frac {mu_{x}}{\sqrt {1-u^{2}/c^{2}}}}$

$p_{y}={\frac {mu_{y}}{\sqrt {1-u^{2}/c^{2}}}}$

$p_{z}={\frac {mu_{z}}{\sqrt {1-u^{2}/c^{2}}}}$

因此，动量的分量取决于相应的速度分量和速度。

由于带有平方根的因子写起来很麻烦，所以经常使用以下缩写，称为洛伦兹伽马因子：

$\gamma ={\frac {1}{\sqrt {1-u^{2}/c^{2}}}}$

动量的表达式然后写成 $\mathbf {p} =m\gamma \mathbf {u}$.

从上面的讨论可以看出，我们可以将以速度 $\mathbf {u}$ 运动的物体的动量写成速度 $u$ 的函数 $M(u)$ 和速度 $\mathbf {u}$ 的乘积：

$M(u)\mathbf {u}$

函数 $M(u)$ 必须在低速下简化为物体的质量 $m$，特别是在物体静止时 $M(0)=m$。

关于相对论中“质量”一词的用法存在争议。如果惯性质量是根据动量定义的，那么它确实会随着 $M=\gamma m$ 变化，对于具有静止质量的单个粒子来说，此外，正如将在下面展示的那样，具有静止质量的粒子的能量由 $E=Mc^{2}$ 给出。在关于命名法的争论之前，函数 $M(u)$ 或关系 $M=\gamma m$，被称为“相对论质量”，它在粒子框架中的值被称为“静止质量”或“不变质量”。相对论质量，$M=\gamma m$，会随着速度增加。这两个术语现在在很大程度上已经过时了：“静止质量”今天简称为质量，“相对论质量”通常不再使用，因为正如将在下面关于能量的讨论中看到的那样，它与能量相同，只是单位不同。

力

牛顿第二定律指出作用在粒子上的合力等于其动量变化率。牛顿第二定律的相同形式在相对论力学中仍然成立。相对论的*3 力* 由下式给出

$\mathbf {f} =d\mathbf {p} /dt$

如果使用相对论质量

${\frac {d\mathbf {p} }{dt}}={\frac {d(m\mathbf {u} )}{dt}}$

根据莱布尼兹定律，其中 $d(xy)=xdy+ydx$

$\mathbf {f} ={\frac {d\mathbf {p} }{dt}}=m{\frac {d\mathbf {u} }{dt}}+\mathbf {u} {\frac {dm}{dt}}$

这个关于力的方程将在下面用来推导出粒子能量的相对论表达式，这些表达式基于“相对论质量”的旧概念。

相对论力也可以用加速度来表示。牛顿第二定律可以写成熟悉的形式

$\mathbf {F} =m\mathbf {a}$

其中 $\mathbf {a} =d\mathbf {v} /dt$ 是加速度。

这里的 m 不是 相对论质量，而是不变质量。

在相对论力学中，动量为 $\mathbf {p} =m\gamma \mathbf {v}$

其中 m 是不变质量，力由 $\mathbf {F} ={\frac {d\mathbf {p} }{dt}}=m{\frac {d(\gamma \mathbf {v} )}{dt}}$

这种力的形式被用于推导出能量表达式，而无需依赖相对论质量。

在本书的第二部分，我们将看到，牛顿第二定律用加速度表示为

$\mathbf {F} =m\gamma (\mathbf {a} +{\frac {\gamma ^{2}v}{c^{2}}}{\frac {dv}{dt}}\mathbf {v} )$

能量

关于使用“相对论质量”概念的争论意味着现代物理课程可能禁止在能量推导中使用它。使用相对论质量的较新能量推导在第一部分给出，而使用相对论质量的较旧推导在第二部分给出。这两种推导可以进行比较，以深入了解关于质量的争论，但真正需要了解 4 向量才能深入讨论这个问题。原则上，第一个推导在数学上是最正确的，因为“相对论质量”由下式给出：$M={\frac {m}{\sqrt {1-u^{2}/c^{2}}}}$，其中包含常数 $m$ 和 $c$.

使用相对论动量推导相对论能量

在下文中，现代推导中，m 表示不变质量——过去称为“静止质量”。能量被定义为将物体从一个地方移动到另一个地方所做的功。我们将使用相对论动量 $p=\gamma mv$。能量由下式给出

$dE=\mathbf {f} d\mathbf {x}$

因此，在整个路径上

$E=\int _{0}^{x}\mathbf {f} d\mathbf {x}$

动能 (K) 是将物体从速度 0 移动到速度 $\mathbf {u}$ 所使用的能量。将运动限制在一个维度

$K=\int _{u=0}^{u=u}\mathbf {f} dx$

使用相对论的 *3 力*

$K=\int _{u=0}^{u=u}{\frac {d(m\gamma u)}{dt}}dx=\int _{u=0}^{u=u}m{\frac {d(\gamma u)}{dt}}dx=\int _{u=0}^{u=u}md(\gamma u){\frac {dx}{dt}}$

用 $d(\gamma u)$ 代替，并使用 $dx/dt=u$

$K=\int _{u=0}^{u=u}m(\gamma du+ud\gamma )u$

这将给出

$K=\int _{u=0}^{u=u}m(u\gamma du+u^{2}d\gamma )$

洛伦兹因子 $\gamma$ 由以下给出

$\gamma ={\frac {1}{\sqrt {1-u^{2}/c^{2}}}}$

意味着

$d\gamma ={\frac {u}{c^{2}}}\gamma ^{3}du$

$du={\frac {c^{2}}{u\gamma ^{3}}}d\gamma$

所以

$K=\int _{\gamma =1}^{\gamma =\gamma }m(u\gamma {\frac {c^{2}}{u\gamma ^{3}}}d\gamma +u^{2}d\gamma )=\int _{\gamma =1}^{\gamma =\gamma }m({\frac {c^{2}}{\gamma ^{2}}}+u^{2})d\gamma =\int _{\gamma =1}^{\gamma =\gamma }mc^{2}d\gamma$

或者，我们可以利用以下事实

$\gamma ^{2}c^{2}-\gamma ^{2}u^{2}=c^{2}\,$

求导

$2\gamma c^{2}d\gamma -\gamma ^{2}2udu-u^{2}2\gamma d\gamma =0\,$

所以，重新整理

$\gamma udu+u^{2}d\gamma =c^{2}d\gamma \,$

在这种情况下

$K=\int _{u=0}^{u=u}m(u\gamma du+u^{2}d\gamma )=\int _{u=0}^{u=u}mc^{2}d\gamma \,$

当 $u$ 从 0 到 $u$ 变化时，洛伦兹因子 $\gamma$ 从 1 到 $\gamma$ 变化，所以

$K=mc^{2}\int _{\gamma =1}^{\gamma =\gamma }d\gamma \,$

因此

$K=\gamma mc^{2}-mc^{2}\,$

量 $\gamma mc^{2}$ 称为粒子的总能量。量 $mc^{2}$ 称为粒子的静止能量。如果粒子的总能量用符号 $E$ 表示

$E=\gamma mc^{2}=mc^{2}+K\,$

因此可以看出 $mc^{2}$ 是静止质量的能量。这种能量被称为质量能。

牛顿近似动能可以通过使用二项式定理展开 $\gamma =(1-u^{2}/c^{2})^{-{\frac {1}{2}}}$ 推导出来。

二项式展开为

$(a+x)^{n}=a^{n}+na^{n-1}x+{\frac {n(n-1)}{2!}}a^{n-2}x^{2}....$

因此，展开 $(1-u^{2}/c^{2})^{-{\frac {1}{2}}}$

$K={\frac {1}{2}}mu^{2}+{\frac {3mu^{4}}{8c^{2}}}+{\frac {5mu^{6}}{16c^{4}}}+...$

因此，如果$u$远小于$c$

$K={\frac {1}{2}}mu^{2}$

这是低速下的牛顿近似值。

利用相对论质量概念推导相对论能量

能量定义为将物体从一个地方移动到另一个地方所做的功。能量来自

$dE=\mathbf {F} d\mathbf {x}$

因此，在整个路径上

$E=\int _{0}^{x}\mathbf {F} d\mathbf {x}$

动能（K）是将物体从速度为 0 移动到速度为$u$所需的能量。因此

$K=\int _{u=0}^{u=u}Fdx$

使用相对论力

$K=\int _{u=0}^{u=u}{\frac {d(Mu)}{dt}}dx$

所以

$K=\int _{u=0}^{u=u}d(Mu){\frac {dx}{dt}}$

将$d(Mu)$代入并使用$dx/dt=u$

$K=\int _{u=0}^{u=u}(Mdu+udM)u$

这将给出

$K=\int _{u=0}^{u=u}(Mudu+u^{2}dM)$

相对论质量由下式给出

$M={\frac {m}{\sqrt {1-u^{2}/c^{2}}}}$

可以扩展为

$M^{2}c^{2}-M^{2}u^{2}=m^{2}c^{2}$

求导

$2Mc^{2}dM-M^{2}2udu-u^{2}2MdM=0$

所以，重新整理

$Mudu+u^{2}dM=c^{2}dM$

在这种情况下

$K=\int _{u=0}^{u=u}(Mudu+u^{2}dM)$

可以简化为

$K=\int _{u=0}^{u=u}c^{2}dM$

但质量从 $m$ 变为 $M$，所以

$K=c^{2}\int _{M=m}^{M=M}dM)$

因此

$K=Mc^{2}-mc^{2}$

数量 $Mc^{2}$ 被称为粒子的总能量。数量 $mc^{2}$ 被称为粒子的静止能量。如果粒子的总能量用符号 $E$ 表示

$E=mc^{2}+K$

因此可以看出 $mc^{2}$ 是静止质量的能量。这种能量被称为质量能，是著名的公式 $E=mc^{2}$ 的起源，该公式是原子时代的标志性公式。

可以通过用静止质量代替相对论质量来推导出动能的牛顿近似，即

$M={\frac {m}{\sqrt {1-u^{2}/c^{2}}}}$

以及

$K=Mc^{2}-mc^{2}$

所以

$K={\frac {mc^{2}}{\sqrt {1-u^{2}/c^{2}}}}-mc^{2}$

即

$K=mc^{2}((1-u^{2}/c^{2})^{-{\frac {1}{2}}}-1)$

可以使用二项式定理展开 $(1-u^{2}/c^{2})^{-{\frac {1}{2}}}$

二项式定理是

$(a+x)^{n}=a^{n}+na^{n-1}x+{\frac {n(n-1)}{2!}}a^{n-2}x^{2}....$

因此，展开 $(1-u^{2}/c^{2})^{-{\frac {1}{2}}}$

$K={\frac {1}{2}}mu^{2}+{\frac {3mu^{4}}{8c^{2}}}+{\frac {5mu^{6}}{16c^{4}}}+...$

因此，如果$u$远小于$c$

$K={\frac {1}{2}}mu^{2}$

这是低速下的牛顿近似。

核能

当质子和中子（核子）结合形成元素时，粒子结合后的状态往往比自由中子和质子具有更低的能量状态。铁具有最低的能量，而铁在原子质量尺度上上下方的元素往往具有更高的能量。这种随着中子和质子结合而能量降低的现象被称为 **结合能**。元素的原子质量略微偏离了其组成粒子计算出的原子质量，这种质量能量差，从 $E=mc^{2}$ 计算，几乎完全等于结合能。

结合能可以通过将每个核子质量更高的元素转化为每个核子质量更低的元素来释放。这可以通过两种方式实现：一是将铀等重元素裂变为钡和氪等轻元素，二是将氢等轻元素聚变为氘等重元素。如果原子被分裂，这个过程被称为 **核裂变**；如果原子被合并，这个过程被称为 **核聚变**。比铁轻的原子可以发生聚变释放能量，而比铁重的原子可以发生裂变释放能量。

当氢和中子结合形成氘时，释放的能量可以按如下方式计算：

质子的质量为 1.00731 amu，中子的质量为 1.00867 amu，氘核的质量为 2.0136 amu。氘核与其组成粒子之间质量差为 0.00238 amu。这个质量差对应的能量为

$E=mc^{2}=1.66\times 10^{-27}\times 0.00238\times (3\times 10^{8})^{2}$

所以释放的能量为 $3.57\times 10^{-13}$ 焦耳，大约是 $2\times 10^{11}$ 焦耳每克质子（电离氢）。

(假设 1 amu = $1.66\times 10^{-27}$ 千克，阿伏伽德罗常数 = $6\times 10^{23}$，光速为 $3\times 10^{8}$ 米每秒)

现在的核反应堆使用一种被称为 **核裂变** 的过程，其中铀棒释放中子，这些中子与铀棒中的铀结合产生铀同位素，例如 ²³⁶U，它会迅速衰变为更小的原子核，例如钡和氪，以及三个中子，这些中子会导致更多 ²³⁶U 的产生和进一步的衰变。每个中子可以引起三个中子的产生，这意味着可以发生 **链式反应**。能量的产生源于质量和能量的等价性；衰变产物钡和氪的质量比原来的 ²³⁶U 低，缺少的质量以 177 MeV 的辐射形式释放。²³⁶U 衰变的核反应方程式如下：

$_{92}^{236}U\rightarrow _{56}^{144}Ba+_{36}^{89}Kr+3n+177MeV$

核爆炸

如果大量的铀同位素 ²³⁵U（**临界质量**）被限制在一个封闭的空间内，链式反应就会失控，并几乎瞬间释放大量的能量。一种限制临界质量铀的装置被称为 **原子弹** 或 **A 武器**。一种基于氘原子聚变的炸弹被称为 **热核弹**、**氢弹** 或 **H 武器**。