狭义相对论/同时性、时间膨胀和长度收缩

狭义相对论

关于同时性的相对性的更多信息

大多数物理理论假设可以同步时钟。如果您在一个空间体积内设置一个同步时钟阵列，并同时对其进行快照，您会发现最靠近您的时钟显示的时间比其他时钟晚，这是由于光从每个遥远的时钟传播到您需要时间。但是，如果已知正确的时钟位置，通过考虑光的传输时间，可以很容易地补偿这些差异并正确同步时钟。同步时钟的可能性存在于光速是恒定的，并且这个恒定速度可以用于同步过程（使用可预测的延迟，当光用于同步时钟时，被称为“爱因斯坦同步”）。

时间上的洛伦兹变换比较了任何时刻同步时钟的读数。它比较了时钟上的实际读数，考虑了观察者之间传输信息所需的任何时间延迟，并回答了“另一个观察者的时钟现在，在这个时刻，实际读数是多少”的问题。这个问题的答案令人震惊。时间上的洛伦兹变换表明，任何相对于您移动的参考系中的时钟都停止同步！

相对运动观察者之间的不同步在下面用一个更简单的图表说明。

同时性的相对性的影响是让每个观察者认为一组不同的事件是同时发生的。时钟之间的相对论相位差（“相对论相位”）意味着相对于彼此移动的观察者具有不同的同时发生事件集，或者是在他们的“现在时刻”。正是这种时间不再是绝对的发现深深地困扰了许多相对论的学生。

时钟在两个观察者之间相差多少取决于时钟到观察者的距离（ $t=xv/c^{2}$ ）。请注意，如果两个观察者都是惯性参考系的一部分，并且时钟在空间的每个点都同步，那么可以通过简单地读取远处点的时钟和原点时钟之间的差来获得相位差。这种差异对两个观察者来说都具有相同的值。

示例：闪烁的灯光

两个相对于彼此静止的灯光相隔 3000 米。这些灯光一个接一个地闪烁，闪烁之间的时间间隔为 4 微秒。你需要以多快的速度沿着灯光的线移动才能看到灯光同时闪烁？

这个问题是相对论相位的直接例子，对于运动的观察者来说是同时发生的事件，在他们自己的参考系中是连续的事件。具有距离的时钟之间的相位差由下式给出

$\Delta t=vx/c^{2}$

所以 $v=\Delta tc^{2}/x$

除以 $c$ 将 $v$ 表示为光速的一部分，得到

$v_{c}=\Delta tc/x$

因此： $v_{c}={\frac {4\times 10^{-6}\times 3\times 10^{8}}{3\times 10^{3}}}$

因此 $v_{c}=0.4c$

（参见 Scherr 等人 (2001) 中的“爆炸”示例）

讨论示例中静止观察者和运动观察者对闪光的时间分配之间的关系：事件时间的洛伦兹变换为 $t'=\gamma (t-vx/c^{2})$ ，它由经过时间 $t$ 和相位差 $vx/c^{2}$ 组成。闪光灯示例的安排是，当两个惯性参考系中的观察者在第一次闪光时彼此相遇时， $t=t'=0$ ，并且 $t=t$ 和 $t'=0$ 是第二次闪光的时间。

如果 $t'=0$ ，那么 $0=\gamma (t-vx/c^{2})$ ，因此，根据洛伦兹变换，当 $t=vx/c^{2}$ 时，运动观察者发现事件在静止惯性参考系中是同时发生的，即：当静止参考系中的经过时间等于两个参考系之间的相位差时。

Scherr, R.E., Shaffer, P.S. and Vokos, S. 学生对狭义相对论中的时间理解：同时性和参考系。物理教育研究，美国物理学杂志增刊，69，S24-35（2001）

示例：相对论捕虫

一艘 1000 米长的宇宙飞船需要以多快的速度航行才能观察到与它船首和船尾对齐的静止时钟之间存在纳秒级的差异？

从 $t=xv/c^{2}$

$10^{-9}=10^{3}v/(9\times 10^{16})$

因此 $v=9\times 10^{4}ms^{-1}$ 或每秒 90 公里。

这种效应可用于将他们在自身惯性参考系中是双胞胎的不同年龄的虫子聚集在一起。

比尔驾驶着一艘非常长的宇宙飞船经过吉姆，并同时捕捉到两只虫子，一只与宇宙飞船的船首重合，一只与船尾重合。尽管这些虫子在它们自身的参考系中是双胞胎，但它们在比尔的参考系中年龄不同。被捕的虫子可以自由地在比尔的宇宙飞船上下游荡，并且可以相遇。

以每秒 90 公里速度航行的宇宙飞船需要多长的长度才能捕捉到图片中的虫子？

仙女座悖论

当我们说事件正在“现在”发生时，我们指的是什么？如果我们正在俯瞰城市景观，观察交通情况，很多事情似乎都在同时发生。我们可以用相机拍一张快照，照片上的场景包含了所有几乎同时发生的事情。它们只是“几乎”在同一时间发生，因为照片上最远处的事件实际上比附近的事件发生得稍早，因为光到达相机需要时间。如果我们想要发现真正同时发生的事件，我们需要减去光到达我们的时间。如果你正在观察月球上的事件，这将是非常必要的：如果你在地球上看到月球钟上的时间，你会知道月球上的实际时间要晚一秒多。但这够了吗？由于运动导致的时钟之间的相对论相位差怎么办？

狭义相对论除了光传播时间之外，还引入了一个因素，它扰乱了我们对哪些事件是同时发生的认识。时钟之间的相对论相位差在月球距离处很小，但在与附近星系一样大的距离处却产生了惊人的结果，即，在地球上驾驶的观察者与站在地球上的另一个人相比，他们可能具有完全不同的事件集与他们的“现在时刻”同时发生。这种相对论相位效应的经典示例是“仙女座悖论”，也称为“Rietdijk-Putnam-Penrose”论证。彭罗斯描述了这个论证：

“两个人在街上相遇；根据其中一个人，仙女座星际舰队已经出发了，而对另一个人来说，决定是否真正开始旅程尚未做出。为什么关于那个决定的结果还存在一些不确定性？如果对任何一个人来说，决定已经做出，那么肯定不会有任何不确定性。太空舰队的发射是不可避免的。”（彭罗斯 1989）。

下面的图示说明了这个论点。

请注意，这两位观察者实际上都无法“看到”现在仙女座上发生的事情。争论的焦点不是关于什么可以“看到”，而是关于不同的观察者认为他们的瞬时现在时刻包含了什么。这两位观察者在望远镜中观察到相同的，两百万年前的事件，但运动的观察者必须假设仙女座上现在的事件比静止的观察者的现在时刻早一两天。（顺便说一下，这两位观察者在望远镜中看到相同的事件，因为从地球到仙女座的距离的长度收缩正好抵消了仙女座上的时间差。）

这个“悖论”引发了关于时间和自由意志本质的相当多的哲学辩论。本书的进阶内容讨论了围绕这种狭义相对论的几何解释的一些问题。

同时性相对论的一个结果是，如果汽车司机发射一枚太空火箭飞往仙女座星系，它可能比从地面发射的太空火箭早出发几天。这是因为对于正在移动的汽车司机来说，与地面上的现在时刻相比，随着距离的增加，他们的“现在时刻”也逐渐提前。下图显示了汽车司机的现在时刻。

仙女座悖论的最终效果是，当一个人向一个遥远的地方移动时，那个地方的事件比没有向那个遥远的地方移动的人的事件发生得晚。两个人现在时刻的事件之间存在一个时间间隔。

双生子悖论

“双生子悖论”来源于朗之万（1911 年）的一篇文章，他在文章中用前往遥远恒星再返回的旅行来描述不同惯性参考系中的时间关系。朗之万最初的例子被称为“时钟悖论”，它表明，一个前往遥远恒星再返回的太空旅行者发现，他的衰老程度比留在地球上的人要少。Benguigui（2012 年）详细描述了随着时间的推移，这个例子是如何演变成两个双胞胎的故事，一个进入太空旅行，一个留在家里，以及韦尔（1922 年）如何将它描述为“双生子悖论”。“双生子悖论”是同时性相对论和时间膨胀的一个有趣的例子，值得仔细研究，以便理解狭义相对论的这些特征。但是请注意，“双生子悖论”之所以引起如此多的困惑，是因为虽然表面上看起来很简单，但分析各个惯性参考系却很复杂。

单程旅行

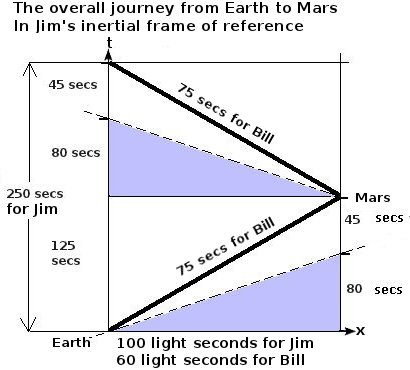
双生子“悖论”包括两个旅程，一个外向旅程和一个返回旅程。通过考虑没有返回的只是外向旅程，可以学到很多关于同时性相对论的知识。单程旅行，没有返回，可能包括以下场景：吉姆留在地球上，比尔乘坐宇宙飞船离开，比尔以 0.8c 的速度飞过吉姆，他们都在相遇时将自己的时钟设置为零，比尔直飞火星，在那里他放下一个记录了他时钟读数的东西。留在地球上的吉姆发现，比尔在旅途中的时钟记录的时间比他自己的时间少。

前往火星的旅程包括两个惯性参考系。在吉姆的参考系中，比尔在移动，吉姆是静止的。在比尔的参考系中，吉姆、地球和火星在移动，比尔是静止的。只有两个参考系，所以诸如“如果吉姆认为自己正在移动，他会观察到什么”之类的問題等同于问“吉姆在比尔的参考系中如何移动？”。

旅程的开始如下所示

为了便于计算，假设火星距离地球 100 光秒。吉姆对旅程的看法很简单，如下所示

如果火星距离 100 光秒，吉姆会计时比尔的旅程需要 125 秒 ( $100/0.8$ )。相对论时间膨胀会导致比尔的时钟读数为 75 秒，即

比尔的时钟读数将为： $125/\gamma$

其中伽马为： ${\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}=1.667$

所以 $125/1.6667=75$ 秒。

在吉姆的惯性参考系中，当比尔到达火星时，吉姆已经衰老了 125 秒，但由于时间膨胀，比尔只衰老了 75 秒。

比尔的这种没有衰老的原因看起来很像悖论，因为人们可能会认为吉姆也应该比比尔衰老得少，毕竟，吉姆远离比尔的程度与比尔远离吉姆的程度一样，所以比尔应该发现吉姆比自己衰老得少，就像吉姆发现比尔比自己衰老得少一样。事实上，这里没有悖论，因为比尔和吉姆对旅程的理解非常不同。比尔对旅程的看法如下所示。

由于相对论相位，比尔发现火星上的时钟比他自己的时钟提前了 80 秒。火星时钟在旅程中又记录了 45 秒。45 秒的旅程时间是比尔在考虑时间膨胀后的预期时间（即： $75/\gamma =75/1.6667=45$ 秒）。更令人惊讶的是，当比尔考虑地球上吉姆的时钟读数时，他发现在地球上吉姆的时钟在旅程中只过去了 45 秒，因为 80 秒的相对论相位差意味着，当比尔经过火星时，他的时钟与地球上发生的事情是同时的，而地球上发生的事件只比他经过地球晚 45 秒。

如果比尔有一艘非常长的火箭，他可以使用“相对论捕虫”的变体（见上文）来捕捉吉姆的一只时钟，就在比尔到达火星的瞬间。然后比尔可以证明在地球上有一个吉姆，他的时钟在比尔的惯性参考系中只过去了 45 秒。如果比尔捕捉了吉姆的一只时钟，那个与比尔经过火星的时刻在他的自己的参考系中是同时的吉姆会记得，一艘宇宙飞船的尾部有一张巨大的网落下，在比尔经过他 45 秒后，网抓住了他的时钟。

请注意，在这个故事中有两个吉姆，一个与比尔访问的火星同时，另一个与比尔在比尔的参考系中同时。与比尔在比尔的参考系中同时的那个吉姆，比那个与比尔到达时火星在他自己的参考系中同时的吉姆要早。

单程旅行是对称的，因为吉姆观察到比尔在旅途中的衰老程度比自己少，比尔也观察到一个更早的吉姆比自己衰老程度少。

如果比尔继续经过火星，直到他的时钟显示经过了 125 秒，那么单程旅行将变得完全对称，这时他会评估吉姆经历了 75 秒的经过时间。当吉姆的时钟显示 125 秒时，吉姆发现比尔的时钟显示 75 秒，对称地，当比尔的时钟显示 125 秒时，比尔发现吉姆的时钟显示 75 秒。这种对称性在下图的示意图中得到了强调，该图比较了吉姆和比尔的时钟读数。

速度变化时会发生什么？

在上一节中，我们已经证明，当观察者以恒定速度分离时，时间膨胀是对称的。这种对称性体现在，在单程旅行中，吉姆观察到比尔的时钟变慢，而比尔也观察到吉姆的时钟变慢。观察者之间的对称性意味着，比尔可以把自己看成是静止的，观察吉姆离开，反之亦然。

比尔发现，有两个吉姆在不同的时间参与了前往火星然后突然改变方向返回地球的旅程：它们在图中标记为 A 和 C。第一个吉姆的时钟显示从比尔经过地球起已经过去了 45 秒，这是在比尔的参考系中与比尔同时经过火星的吉姆。第二个吉姆的时钟显示从遇到比尔起已经过去了 205 秒，这个吉姆在比尔的参考系中与比尔同时到达火星并以 -0.8c 的速度开始返回地球的旅程。

由于不存在一个与比尔在速度变化时同时存在的吉姆，这在狭义相对论中引入了不对称性。比尔在火星转向返回地球并不等同于地球转向迎接比尔，因为直到比尔转向之前，尚不清楚是哪个地球和哪个吉姆在进行旅程。首次提出旅行者离开并返回时变年轻的例子的朗之万 (1911) 非常清楚地认识到这种不对称性，并指出：“因此，不对称性——由于只有旅行者，在他的旅程中途，经历了改变其速度方向的加速度”。

在狭义相对论中，物理定律对惯性参考系中的每个观察者来说都是相同的。惯性参考系可以是船上房间或整个城市的所有时钟和测量棒，惯性参考系的关键特征是时钟和测量棒彼此静止。运动的测量方式是，宇宙的其余部分相对于观察者的惯性参考系运动。在比尔前往火星并返回地球的例子中，有三个惯性参考系：吉姆、外向的比尔和内向的比尔。外向的比尔和内向的比尔之间隔着一段比尔转向时速度变化的时期。这段速度变化时期也可以看作是比尔单一惯性参考系中的一个非惯性间断，在此之后，比尔的时钟和测量棒与宇宙中其他部分的关系发生了变化。

诸如“如果转向后与比尔同时存在的吉姆把自己看成是朝比尔运动，他会如何看待事件？”这样的问题实际上是关于内向的比尔的参考系。在吉姆自己的惯性参考系中，比尔只是去火星，转身回来。吉姆总是把自己看成是静止的，除非他的参考系通过经历速度变化而变得非惯性，在这种情况下，吉姆会把自己看成是从一个静止状态移动到另一个与宇宙具有不同关系的静止状态。狭义相对论认为物理定律在所有惯性参考系中都是相同的，它并不认为所有运动都是相对的，即使在非惯性变化中也是如此。

与比尔到达火星时同时存在的吉姆和比尔开始返回地球旅程时同时存在的吉姆之间的时间间隔被称为“时间间隔”。“双生子佯谬”中的时间间隔包含了外向和内向阶段差的总和，在本例中，时间间隔为 160 秒。

“双生子佯谬”的时间间隔描述

一旦接受比尔和吉姆对旅程有截然不同的看法，这些看法就可以在“时间间隔”描述中总结出来。在这种描述中，比尔飞往火星并发现那里的时钟比他自己的时钟显示的时间晚。他转身飞回地球，并意识到同时性的相对性意味着，对比尔来说，地球上的时钟会向前跳跃，并且比火星上的时钟超前，又出现了一个“时间间隔”。当比尔回到地球时，时间间隔和时间膨胀意味着地球上的人记录了比他记录的更多的时钟滴答声。

为了便于计算，假设比尔以惊人的速度 0.8c 朝向一个距离 100 光秒（约 3000 万公里）的遥远点运动。下面的插图显示了吉姆和比尔的观察结果

从比尔的观点来看，存在时间膨胀和相位效应。正是“相位”的附加因素解释了为什么，尽管时间膨胀对两个观察者都发生，但比尔在整个旅程中观察到吉姆的时钟上的读数与吉姆相同。

总结使用该示例解释“双生子佯谬”的数学公式

吉姆观察到的距离为 100 光秒，遥远点在他的参考系中。根据吉姆的说法，比尔完成旅程所需的时间为

所需时间 = 距离 / 速度，因此根据吉姆的说法

t=100/0.8=125

秒

同样根据吉姆的说法，时间膨胀应该影响比尔的时钟上观察到的时间

T=t\times {\sqrt {1-v^{2}/c^{2}}}

所以

T=125\times {\sqrt {1-0.8^{2}}}=75

秒

因此，对吉姆来说，往返行程需要 250 秒，比尔的时钟显示 150 秒。

比尔测量的距离为

X=x\times {\sqrt {1-v^{2}/c^{2}}}=100\times {\sqrt {1-0.8^{2}}}=60

光秒。

对比尔来说，需要

X/v=60/0.8=75

秒。

比尔观察到吉姆的时钟由于时间膨胀而显得运行缓慢

t^{'}=T\times {\sqrt {1-v^{2}/c^{2}}}

所以

t^{'}=75\times {\sqrt {1-0.8^{2}}}=45

秒。

但也有一个时间差为 $vx/c^{2}=80$ 秒。

因此，对于比尔来说，吉姆的时钟从起点到远点记录了 125 秒。这包括吉姆时钟在转向点经过的 45 秒，以及旅程开始时的 80 秒时间差。比尔观察到，吉姆的时钟在整个旅程中记录了总计 250 秒，这与吉姆在自己的时钟上观察到的一样。

进一步阅读

Benguigui, L (2012). 两对双胞胎的故事。arXiv:1212.4414v1

Bohm, D. 狭义相对论（W. A. Benjamin，1965）。

D’Inverno, R. 迈入爱因斯坦的相对论（牛津大学出版社，1992）。

Eagle, A. 关于 Dolby 和 Gull 关于雷达时间和双胞胎“悖论”的注记。美国物理学杂志。2005 年，第 73 卷；第 10 期，第 976-978 页。http://arxiv.org/PS_cache/physics/pdf/0411/0411008v2.pdf

Langevin, P. (1911) 空间和时间的演变 Scientia 10 (1911), 31-34

长度收缩的本质

根据狭义相对论，像测量杆这样的物体由分布在空间和时间中的事件组成，而一个三维杆是构成杆在单个时刻的事件。然而，从同时性的相对性可以明显看出，两个相对运动的观察者将拥有不同的事件集，这些事件集在给定的时刻存在。这意味着，两个相对于彼此运动的观察者通常会观察到由**不同**的事件集组成的测量杆。如果“杆”这个词指的是被称为杆的三维形式，那么这两个相对运动的观察者将**观察到不同的杆**。

可以使用闵可夫斯基图来查看测量杆在观察者之间不同的方式。闵可夫斯基图中对应于构成物体在一段时间内的所有事件的区域被称为该物体的**世界线**。从下面的图像可以看出，长度收缩是由于各个观察者在他们的现在时刻拥有物体世界线不同的部分的结果。

（应该记住，时空图上的最长长度通常在现实中是最短的）。

有时人们说，长度收缩发生是因为物体旋转到时间轴上。这实际上是一个半真半假的答案，三维杆实际上并没有旋转，而是观察到的四维杆的三维切片发生了变化，使得它看起来像是杆旋转到时间轴上。在狭义相对论中，不是杆旋转到时间轴上，而是观察者对杆世界线的切片旋转。

毫无疑问，杆世界线的切片对于相对运动的观察者来说确实有不同的长度。组成杆世界线的事件是否总是存在，这是一个哲学思辨的问题。

进一步阅读

Vesselin Petkov. (2005) 存在一种替代块宇宙观的方案吗？

Dragan V Redžić (2010). 相对论长度之苦的延续

杆仓悖论

相对论中的长度收缩是对称的。当两个相对运动的观察者彼此经过时，他们都测量到长度的收缩。

（注意，闵可夫斯基度量涉及时间的位移的减法，因此，在二维纸张上看起来最长的长度在 (3+1)D 现实中往往是最短的长度）。

长度收缩的对称性导致了两个问题。首先，一系列事件如何被另一个观察者观察到是同时发生的事件？这个问题导致了德布罗意波和量子理论的概念。其次，如果一个杆在一个参考系中同时位于两个点之间，那么它如何在另一个参考系中被观察到依次位于这两个点之间？例如，如果一个杆以高速进入一栋建筑，一个观察者如何发现它完全在建筑物内，而另一个观察者发现杆的两端在不同的时间分别与建筑物两端相对？如果杆撞到建筑物的末端会发生什么？第二个问题被称为“杆仓悖论”或“梯子悖论”。

杆仓悖论陈述如下：假设一个以 0.75c 的速度奔跑并携带一根 15 米长的水平杆走向一个长 10 米的谷仓，谷仓有前后两个门。当跑步者和杆进入谷仓时，地面观察者关闭然后打开两扇门（通过遥控），使跑步者和杆暂时被困在谷仓内，然后从后门走出谷仓。

人们可能会惊讶地看到一根 15 米长的杆能装进一个 10 米长的谷仓。但是，杆相对于地面观察者处于运动状态，地面观察者测得杆的长度收缩到 9.9 米（使用方程检查）。

当我们考虑跑步者的观点时，“悖论”就出现了。跑步者看到谷仓收缩到 6.6 米。因为杆处于跑步者的静止参考系中，所以跑步者测量到它的长度是 15 米。现在，我们如何才能让我们的超级英雄安全地穿过谷仓？

“悖论”的解决在于同时性的相对性。地面观察者测量到两扇门的关闭是同时发生的。然而，由于两个门位于不同的位置，所以跑步者说它们不是同时关闭的。后门先关闭然后打开，让杆的前端离开。谷仓的前门直到杆的后端经过时才关闭。

如果后门保持关闭并由某种不可穿透的材料制成会发生什么？我们能否通过在杆完全在谷仓内时关闭前门来将杆困在谷仓内，这是根据地面观察者的说法？当杆的前端撞到后门时，关于这种撞击的信息将以冲击波的形式沿杆向后传播。信息不能以超过 c 的速度传播，因此杆的后端将继续以其原始速度向前运动，直到波到达它。即使冲击波以光速传播，它也不会在杆的后端经过前门之后到达杆的后端，即使在跑步者的参考系中也是如此。因此，当前门关闭时，整个杆（虽然非常压缩）将在谷仓内。如果它是无限弹性的，它最终会被压缩并“弹簧加载”到封闭谷仓的内部。

长度收缩的证据，无限直电流的场

长度收缩可以在无限长直电流的场中直接观察到。下图展示了这种情况。

非相对论电磁学使用以下公式描述由于电荷产生的电场

$E={\frac {\lambda }{2\pi \epsilon _{0}r}}$

并使用毕奥-萨伐尔定律描述由无限长直电流产生的磁场

$B={\frac {\mu _{0}I}{2\pi r}}$

或者使用电荷密度（从 $I=\lambda v$ 其中 $\lambda$ 是单位长度上的电荷量)

$B={\frac {\mu _{0}\lambda v}{2\pi r}}$

利用相对论，可以证明上述磁场公式可以通过对电场的长度收缩的相对论效应来推导出来，因此我们所说的“磁场”可以理解为对单一现象的相对论观察结果。相对论计算如下。

如果 Jim 相对于导线以与负电荷相同的速度运动，他会看到导线相对于 Bill 发生收缩。

$l_{+}=l{\sqrt {1-v^{2}/c^{2}}}$

Bill 应该看到沿导线运动的电荷之间的空间也收缩了相同的量，但电中性的要求意味着运动的电荷将被分散以匹配导线中固定电荷的参考系。

这意味着 Jim 看到负电荷被分散，使得

$l_{-}={\frac {l}{\sqrt {1-v^{2}/c^{2}}}}$

Jim 观察到的净电荷密度为

$\lambda ={\frac {q}{l_{-}}}-{\frac {q}{l_{+}}}$

代入

$\lambda ={\frac {q}{l}}({\sqrt {1-v^{2}/c^{2}}}-{\frac {1}{\sqrt {1-v^{2}/c^{2}}}})$

使用二项式展开

$\lambda ={\frac {q}{l}}(1-{\frac {v^{2}}{2c^{2}}}-1-{\frac {v^{2}}{2c^{2}}})$

因此，考虑到净正电荷，正电荷是固定的

$\lambda ={\frac {qv^{2}}{lc^{2}}}$

Jim 位置处的电场由下式给出

$E={\frac {\lambda v^{2}}{2\pi \epsilon _{0}rc^{2}}}$

吉姆所在位置的电场力由 $F=Eq$ 给出，即

$F={\frac {q\lambda v^{2}}{2\pi \epsilon _{0}rc^{2}}}$

现在，根据经典电磁学

$c^{2}={\frac {1}{\epsilon _{0}\mu _{0}}}$

所以将此代入 $F={\frac {q\lambda v^{2}}{2\pi \epsilon _{0}rc^{2}}}$

(1) $F={\frac {q\mu _{0}\lambda v^{2}}{2\pi r}}$

这是比尔观察到的相对论电场力的公式，它表现为磁力。这与非相对论磁力计算结果如何比较？根据经典公式，吉姆位置上的电荷受到的磁场力为

$F=Bqv$

根据毕奥-萨伐尔定律，该力为

(2) $F={\frac {q\mu _{0}\lambda v^{2}}{2\pi r}}$

这表明吉姆所经历的相对论电场力的公式与经典磁力公式相同。

可以看出，一旦理解了时空的概念，这两个场的统一就变得简单明了。吉姆相对于导线以与负电荷载流子相同的速度运动，所以吉姆只感受到电场。比尔相对于导线是静止的，他观察到导线中的电荷是平衡的，而吉姆观察到电荷不平衡。比尔将吉姆与载流子之间的吸引归因于“磁场”。

重要的是要注意，与上面给出的长度收缩解释一样，构成吉姆负电荷流的事件与构成比尔负电荷流的事件不同。比尔和吉姆的负电荷占据了时间上的不同时刻。

顺便说一句，导线中电子的漂移速度约为每秒一毫米，但导线中存在大量的电荷（参见下面的链接）。

进一步阅读

Purcell, E. M. 电和磁。伯克利物理课程。第 2 卷。第 2 版。纽约，纽约：麦格劳-希尔。1984 年。ISBN: 0070049084。

有用链接

http://hyperphysics.phy-astr.gsu.edu/hbase/electric/ohmmic.html

http://hyperphysics.phy-astr.gsu.edu/hbase/relativ/releng.html

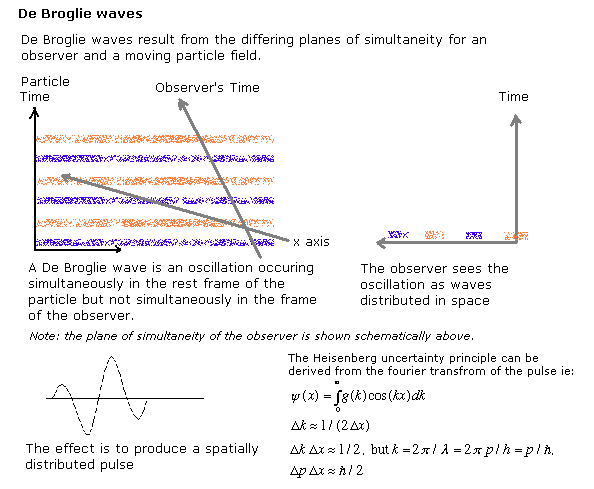
德布罗意波

德布罗意注意到，宇宙的不同三维部分会导致观察者的静止系中的振荡在运动的观察者的静止系中表现为波列。

他将这一洞察与爱因斯坦关于能量量子化的思想结合起来，为量子理论奠定了基础。德布罗意的洞察力也是对上面给出的长度收缩描述的间接证明——相对运动的观察者拥有四维宇宙中不同的三维切片。物质波的存在是同时性相对性的直接实验证据。

进一步阅读：de Broglie, L. (1925) 关于量子理论。RECHERCHES SUR LA THEORIE DES QUANTA（Ann. de Phys., 10e s´erie, t. III (Janvier-F ´evrier 1925)）的翻译。作者：A. F. Kracklauer。 http://replay.web.archive.org/20090509012910/http://www.ensmp.fr/aflb/LDB-oeuvres/De_Broglie_Kracklauer.pdf

贝尔飞船悖论

贝尔设计了一个思想实验，称为“宇宙飞船悖论”，以探究长度收缩是否涉及力以及这种收缩是否是空间的收缩。在宇宙飞船悖论中，两艘宇宙飞船由一根细而硬的绳子连接，并且都以相等的线性加速度加速到速度 $v$ 相对于地面，在该速度下，在狭义相对论版本的悖论中，加速度停止。两艘宇宙飞船的加速度被安排成根据地面观察者相等，因此，根据地面观察者，宇宙飞船将保持相同的距离。问题是绳子是否会断裂。

考虑这个问题时，研究一艘宇宙飞船会发生什么是有帮助的。如果一艘具有尾部推进器的宇宙飞船根据地面观察者线性加速到速度 $v$ ，那么地面观察者将观察到它在运动方向上收缩。在收缩期间，宇宙飞船前部的加速度将略小于宇宙飞船后部的加速度，然后在尾部加速度和增加的收缩停止后，突然达到一个高值，使前部和后部的速度相等。从地面观察，可以观察到，总的来说，尾部的加速度可以是线性的，但前部的加速度是非线性的。

在贝尔的思想实验中，两艘宇宙飞船都被人工限制为根据地面观察者具有恒定加速度，直到加速度停止。不允许突然调整。此外，不允许在组件的前部和后部之间的加速度之间存在差异，因此任何收缩趋势都需要作为绳子的张力和伸长来承受。

这个悖论最有趣的部分是宇宙飞船之间的空间发生了什么。从地面观察，宇宙飞船将保持相同的距离（实验被安排来实现这一点），而根据宇宙飞船上的观察者，它们似乎会越来越分开。这意味着加速度在不同的参考系之间不是不变的（见第二部分），并且作用于宇宙飞船的力实际上会受到每个参考系观察到的宇宙飞船分离差异的影响。

上面关于长度收缩本质的部分表明，当绳子的速度发生变化时，地面上的观察者会观察到构成绳子的事件集合发生变化。这些新事件定义了一条比原来更短的绳子。这意味着，从地面观察，绳子确实会试图收缩，并且从宇宙飞船观察，它会在张力下被拉伸。如果绳子无法承受运动参考系中的伸长和张力或静止参考系中的张力，它就会断裂。

贝尔宇宙飞船悖论的另一个有趣方面是，在宇宙飞船的惯性系中，由于同时性的相对性，前导宇宙飞船将始终比后导宇宙飞船运动得略快，因此宇宙飞船-绳索系统在两艘宇宙飞船的参考系中加速度停止之前，不会形成一个真正的惯性参考系。加速度停止的异步性表明，在任何一艘宇宙飞船的参考系中，前导宇宙飞船都比后导宇宙飞船先达到最终速度。然而，这种时间差非常小（小于影响以光速 $x/c>vx/c^{2}$ 在绳索上传播的时间）。

在这个阶段，有必要警告不要将狭义相对论外推到广义相对论 (GR) 的领域。SR 无法自信地应用于加速系统，这就是为什么上面的评论仅限于定性观察。

进一步阅读

贝尔，J. S. (1976)。量子力学中的可言与不可言。剑桥大学出版社 1987 ISBN 0-521-52338-9

Hsu，J-P 和 Suzuki，N. (2005) 加速参考系的扩展洛伦兹变换和“两宇宙飞船悖论”的解 AAPPS 公告 2005 年 10 月 p.17 http://www.aapps.org/archive/bulletin/vol15/15-5/15_5_p17p21%7F.pdf

Matsuda，T 和 Kinoshita，A (2004。狭义相对论中的两艘宇宙飞船的悖论。AAPPS 公告 2004 年 2 月 p3。 http://www.aapps.org/archive/bulletin/vol14/14_1/14_1_p03p07.pdf

横向多普勒效应

时间膨胀的存在意味着从朝向或远离观察者运动的光源发射的光的频率在垂直于运动方向的方向上应该发生红移。横向多普勒效应由下式给出

\nu =\nu ^{\prime }{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}

其中 $\nu$ 是观察到的频率，而 $\nu ^{\prime }$ 是如果光源相对于观察者静止时的频率（**固有频率**）。

这种效应最早由艾夫斯和斯蒂尔韦尔在 1938 年证实。横向多普勒效应是纯粹的相对论效应，已被用作时间膨胀发生的证明示例。

角度的相对论变换

如果一根杆子与其朝向或远离观察者的运动方向成一定角度，则其在运动方向上的长度分量将收缩。这意味着观察到的角度在参考系变化期间也会发生变换。假设运动发生在 x 轴上，假设杆子在静止系中的固有长度（静止长度）为 $L^{\prime }$ 米，并且与 x' 轴成 $\theta ^{\prime }$ 度角。与轴形成的角度的正切为

杆静止参考系中的正切 =

\tan \theta ^{\prime }={\frac {L_{y}^{\prime }}{L_{x}^{\prime }}}

观察者参考系中的正切 =

\tan \theta ={\frac {L_{y}}{L_{x}}}

因此

{\frac {\tan \theta }{\tan \theta ^{\prime }}}={\frac {L_{y}L_{x}^{\prime }}{L_{y}^{\prime }L_{x}}}

但是

L_{x}=L_{x}^{\prime }{\sqrt {1-v^{2}/c^{2}}}

并且

L_{y}=L_{y}^{\prime }

所以

\tan \theta ={\frac {\tan \theta ^{\prime }}{\sqrt {1-v^{2}/c^{2}}}}

表明，观察者观察到的与运动方向成角的角度会随着速度增加。

运动物体与 x 轴所成的角度也涉及速度的变换，以计算正确的入射角。

速度相加

两个以 v 米/秒的速度彼此相对运动的观察者如何比较他们对第三个物体的速度的观察结果？

假设其中一个观察者测得物体的速度为 $u^{'}$ ，其中

$u^{'}={\frac {x^{'}}{t^{'}}}$

坐标 $x^{'}$ 和 $t^{'}$ 由洛伦兹变换给出

$x^{'}={\frac {x-vt}{\sqrt {(1-v^{2}/c^{2})}}}$

和

$t^{'}={\frac {t-(v/c^{2})x}{\sqrt {(1-v^{2}/c^{2})}}}$

但是

$x^{'}=u^{'}t^{'}$

所以

${\frac {x-vt}{\sqrt {(1-v^{2}/c^{2})}}}=u^{'}{\frac {t-(v/c^{2})x}{\sqrt {(1-v^{2}/c^{2})}}}$

因此

$x-vt=u^{'}(t-vx/c^{2})$

注意相位项 $vx/c^{2}$ 的作用。该方程可以改写为

$x={\frac {(u^{'}+v)}{(1+u^{'}v/c^{2})}}t$

鉴于 $x=ut$

$u={\frac {(u^{'}+v)}{(1+u^{'}v/c^{2})}}$

这就是著名的 **相对论速度加法定理**，它适用于平行于相互运动方向的速度。

时间膨胀的存在意味着，即使物体垂直于运动方向运动，相对运动的观察者对物体的速度报告也会出现差异。如果在 x 方向上存在任何速度分量 ( ${u_{x}}$ ， ${{u^{'}}_{x}}$ )，那么相位会影响时间测量，进而影响垂直于 x 轴的速度。下表总结了空间各个方向上的相对论速度加法。

${u^{'}}_{x}={\frac {(u_{x}-v)}{(1-u_{x}v/c^{2})}}$	$u_{x}={\frac {({u^{'}}_{x}+v)}{(1+{u^{'}}_{x}v/c^{2})}}$
${u^{'}}_{y}={\frac {u_{y}{\sqrt {1-v^{2}/c^{2}}}}{(1-u_{x}v/c^{2})}}$	$u_{y}={\frac {{u^{'}}_{y}{\sqrt {1-v^{2}/c^{2}}}}{(1+{u^{'}}_{x}v/c^{2})}}$
${u^{'}}_{z}={\frac {u_{z}{\sqrt {1-v^{2}/c^{2}}}}{(1-u_{x}v/c^{2})}}$	$u_{z}={\frac {{u^{'}}_{z}{\sqrt {1-v^{2}/c^{2}}}}{(1+{u^{'}}_{x}v/c^{2})}}</P>$