狭义相对论/波

狭义相对论

狭义相对论的应用

在本章中，我们将继续研究狭义相对论，将前一章中开发的思想应用于波的研究。

首先，我们将展示如何在时空的背景下描述波。然后我们看到，没有优先参考系（例如支持它们的介质）的波，受狭义相对论的约束，具有特定形式的色散关系。这种色散关系结果是量子力学中相对论物质波的色散关系。

其次，我们将研究多普勒频移现象，其中波的频率在不同的坐标系中取不同的值。

第三，我们将展示如何在相对论上一致地添加速度。这在讨论狭义相对论中的粒子行为时也会很有用。

一个新的数学概念将在相对论波的背景下呈现，即时空向量或四向量。用相对论标量和四向量完全写出物理定律确保它们在所有惯性参考系中都有效。

时空中的波

我们现在看看时空中的波的特征。回想一下，一个空间维度的波可以用

$A(x,t)=A_{0}\sin(kx-\omega t)\,$

其中 $A_{0}$ 是波的（常数）振幅， $k$ 是波数， $\omega$ 是角频率，并且量 $\phi =kx-\omega t$ 被称为波的相位。对于三维空间中的波，波以类似的方式表示，

$A(\mathbf {x} ,t)=A_{0}\sin(\mathbf {k} \cdot \mathbf {x} -\omega t)$

其中 $\mathbf {x}$ 现在是位置向量， $\mathbf {k}$ 是波向量。波向量的幅度， $|\mathbf {k} |=k$ 只是波的波数，该向量的方向表示波移动的方向。在这种情况下，波的相位是 $\phi =\mathbf {k} \cdot \mathbf {x} -\omega t$ .

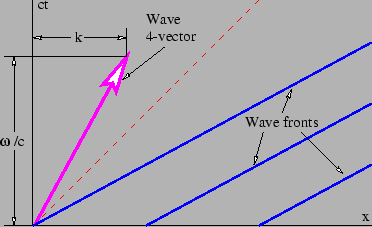Figure 5.1: Sketch of wave fronts for a wave in spacetime.

图 5.1：时空波前示意图。大箭头是相关的波四向量，其斜率为

\omega /ck

。波前的斜率是它的倒数，

ck/\omega

.

在一维情况下 $\phi =kx-\omega t$ 。波前具有恒定相位 $\phi$ ，因此求解这个方程关于 $t$ 并乘以真空中的光速 $c$ ，我们可以得到波前世界线的方程

$ct={\frac {ckx}{\omega }}-{\frac {c\phi }{\omega }}={\frac {cx}{u_{p}}}-{\frac {c\phi }{\omega }}\quad {\mbox{(wave front).}}$

世界线在时空图中的斜率是 $x$ 的系数，或 $c/u_{p}$ ，其中 $u_{p}=\omega /k$ 是相速度。

相对论在波中的应用

回到波的相位，我们立即看到

\phi =\mathbf {k} \cdot \mathbf {x} -\omega t=\mathbf {k} \cdot \mathbf {x} -(\omega /c)(ct)={\underline {k}}\cdot {\underline {x}}.

因此，写波的一种简洁方式是 $A({\underline {x}})=\sin({\underline {k}}\cdot {\underline {x}}).$ (6.8)

由于 ${\underline {x}}$ 已知是四向量，并且波的相位已知是与参考系无关的标量，因此可以得出 ${\underline {k}}$ 实际上是一个四向量，而不仅仅是一组数字。因此，波四向量的长度的平方也必须是与参考系无关的标量

{\underline {k}}\cdot {\underline {k}}=\mathbf {k} \cdot \mathbf {k} -\omega ^{2}/c^{2}=const.

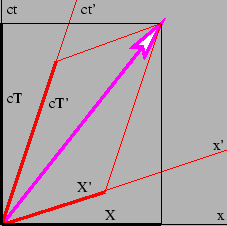
Figure 5.2: Resolution of a four-vector into components in two different reference frames.

四向量在两个不同参考系中的分量分解。

让我们精确地回顾一下这意味着什么。如图所示，我们可以将位置四向量x分解成两个不同参考系中的分量，例如(X,T)和(X′,T′)，但这只是写同一个向量的不同方式。

这与三维向量在旋转系中具有不同的分量完全相同。

类似地，就像三维向量在所有系中具有相同的幅度一样，四向量也是如此；即，

X^{2}-c^{2}T^{2}=X^{\prime 2}-c^{2}T^{\prime 2}

将此应用于波动四矢量，我们可以推断出

k^{2}-c^{-2}\omega ^{2}=k^{\prime 2}-c^{-2}\omega ^{\prime 2}

其中，k 和 ω 的无撇号值和有撇号值分别指波动四矢量在两个不同参考系中的分量。

到目前为止，这个论点适用于任何波。然而，波可以分为两类，一类是存在一个特殊参考系的波，另一类是不存在这种特殊参考系的波。

例如，声波在气体静止的参考系中看起来最简单。光在折射率不等于1的材料介质中传播也是如此。在这两种情况下，只有在材料介质静止的参考系中，波的速度在各个方向上才相同。

如果没有材料介质，就没有明确的方法来找到一个特殊的参考系，因此这些波必须属于第二类。这包括真空中所有波，例如光。

在这种情况下，可以进行以下论证。一个相对于频率为 ω 和波数为 k 的波运动的观察者，看到频率为 ω′ 和波数为 k′ 的波。如果观察者能以任何方式判断这些波来自一个相对于它们运动的源，那么他们就可以利用这一点来识别这些波的特殊参考系，因此这些波看起来就像来自一个频率为 ω 的静止源一样。

这迫使我们得出结论，对于这种波

\omega ^{2}=c^{2}k^{2}+\mu ^{2}\,

其中 μ 是一个常数。真空中所有的波都必须具有这种形式，这比经典物理学中更受限制的选择。

在经典物理学中，光的 ω 和 k 之间的关系为

\omega =ck\,

在相对论物理学中，我们已经看到，对于没有特殊参考系的波（如光），ω 和 k 之间的关系为

\omega ^{2}=c^{2}k^{2}+\mu ^{2}\,

如果 μ=0，则相对论方程简化为经典方程，因此我们可以假设，对于光，μ 确实等于零。

这意味着光没有最低频率。

如果 μ 不为零，则所描述的波是色散波。相速度为

u_{p}={\frac {\omega }{k}}={\sqrt {c^{2}+{\frac {\mu ^{2}}{k^{2}}}}}

这个相速度总是大于 c，这乍看起来似乎是一个非物理的结论。然而，波的群速度为

u_{g}={\frac {d\omega }{dk}}={\frac {kc^{2}}{\sqrt {k^{2}c^{2}+\mu ^{2}}}}={\frac {kc^{2}}{\omega }}={\frac {c^{2}}{u_{p}}}

它总是小于 c。由于波包以及信号以群速度传播，因此即使相速度超过光速，这种类型的波在物理上也是合理的。

这种波的另一个有趣的性质是波动四矢量平行于时空中的波包世界线。以下论证很容易证明这一点。

波动四矢量的空间分量为 k，时间分量为 ω/c。因此，四矢量在时空图上的斜率为 ω/kc。然而，以群速度移动的波包世界线的斜率为 c/u_g，这也等于 ω/kc。

注意，当 k 为零时，我们有 ω=μ。在这种情况下，波的群速度为零。因此，我们有时将 μ 称为波的静止频率。

多普勒效应

你可能听说过火车鸣笛的声音如何随着火车经过你而发生变化。当火车驶近时，音调或频率比火车驶离时高。这被称为多普勒效应。如果你经过一个声源，也会发生类似但不同的效应。如果一个静止的汽笛在鸣叫，从一辆移动的汽车上听到的音调在朝声源移动时比离开时高。因此，第一个案例是运动的声源，而第二个案例是运动的观察者。

在本节中，我们将计算多普勒效应，因为它适用于光在真空中传播。下图显示了计算光波前之间时间的几何形状，用于静止和移动参考系。