桁架是由一系列三角形支撑构成的,没有跨度内的荷载。作为二力杆件,梁只在两端施加力。两端产生的合力的大小必须相等,方向相反,沿着杆件连接点的直线。这些力被称为轴向力。如果 T 为负(即两端的力互相指向),则杆件处于压缩状态;如果 T 为正,则杆件处于拉伸状态。
分析桁架的主要方法有节点法和截面法。
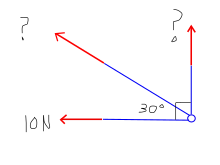 蓝线是桁架的杆件,蓝色圆圈是所有杆件连接的节点
蓝线是桁架的杆件,蓝色圆圈是所有杆件连接的节点
下图展示了一个三杆桁架。图中给出了角度和一个力。利用你所知道的平衡知识,求出垂直杆件和斜杆件的力。
然后指定一个坐标系。在这个问题中,可以使用二维 X,Y 平面,其中正 X 轴为水平方向,从左到右(指向右侧)。Y 轴为垂直方向,指向向上。
由于这是一个静力学问题,节点不能移动。节点不移动的唯一方法是作用在它上面的力处于平衡状态(所有方向的合力必须为零)。现在一个明智的步骤是将节点处的 X 力和 Y 力求和。
指定变量名称,这样你就不会混淆杆件,让我们将垂直杆件的张力称为  ,将斜杆件的张力称为
,将斜杆件的张力称为  .
.


90 度的余弦为零,所以  会消失。你也可以简单地通过注意到
会消失。你也可以简单地通过注意到  没有 X 分量而将它去掉。
没有 X 分量而将它去掉。


负号表示力与图中所示方向相反。这意味着杆件处于压缩状态而不是拉伸状态。现在我们可以求解  .
.



这个答案是正的,这意味着图中所示的方向是正确的,杆件处于拉伸状态。
问题已经解决,我们知道了桁架中每个杆件的力以及杆件是处于拉伸状态还是压缩状态。如果你在形象化问题时遇到困难,看看下面的图片是否对你有帮助。
 这张图片显示了作用在节点上的每个力的正确方向,你可以看到这些力将加起来为零,因此节点不会移动。
这张图片显示了作用在节点上的每个力的正确方向,你可以看到这些力将加起来为零,因此节点不会移动。
快速链接:静力学, 土木工程, 机械工程











