假设你有一个放在地上的箱子,并且这个箱子正被两个方向的特定力拉动。你可以通过找到作用在箱子上的合力来预测箱子的运动。如果每个力向量(其中大小是绳索的张力,方向是绳索“指向”的方向)都可以测量,则可以将这些向量相加以得到合力。有两种方法可以进行向量加法
 两个向量的加法
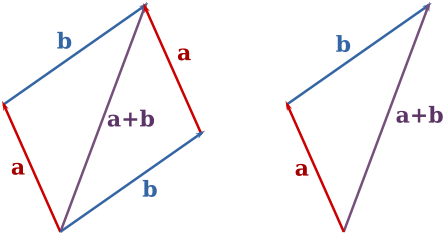
两个向量的加法
这是一种图形化的方法来进行向量加法。首先,一些术语
- 向量的尾部是它起源的地方。
- 向量的头部是它指向的地方。头部是带有箭头的那一端。
这种方法最容易使用绘图纸执行。建立一个直角坐标系,并按比例绘制第一个向量,其尾部位于原点。然后,绘制第二个向量(同样,按比例绘制),使其尾部与第一个向量的头部重合。然后,和向量的属性如下
- 和向量的长度是从原点到第二个向量头部的距离。
- 和向量的方向是角度。
在右侧的图像中,向量 (10, 53°07'48") 和 (10, 36°52'12") 正在以图形方式相加。结果是 (19.80, 45°00'00")。(我如何如此精确地测量出这些角度?我故意这么做的。)
平行四边形法则的原生向量格式是“极坐标形式”。
当使用计算方法时,必须将每个向量分解成其x和y分量。然后,只需将相应的分量相加。
如果一个向量由 (r, θ) 给出,其中r是长度,θ是方向,
如果一个向量由 给出,
给出,


请记住,arctan() 函数仅返回 [-π/2, π/2] 范围内的值;因此,如果你的向量在第二或第三象限,则必须将π添加到从 arctan() 函数返回的任何角度。
再次参考右侧的图像,请注意第一个向量可以表示为 ,第二个等效于
,第二个等效于 。(验证一下。)然后,只需将分量相加
。(验证一下。)然后,只需将分量相加

你应该验证 等于 (19.80, 45°00'00")。
等于 (19.80, 45°00'00")。
有两种方法可以进行向量乘法。我不会在这里深入探讨具体的应用;在阅读本书的过程中,你会看到很多这样的应用。
两个向量的点积的结果是一个标量。点积是分量乘积的和。例如
< 1 , 2 >
∙ < 3 , 4 >
-----------
| +-----> 2 x 4 = 8
+---------> 1 x 3 = 3
------
11
 使用点积计算甲烷等对称四面体分子的键角
使用点积计算甲烷等对称四面体分子的键角
向量、它们的长度以及它们之间角度之间的一个有用关系由点积的定义给出

- 向量
 和
和  。
。
- 向量的大小分别为
 和
和  。
。
- 这两个向量之间的夹角为
 。
。
两个向量的叉积得到另一个向量。叉积仅适用于三维空间向量。请记住三个单位向量
 是沿着 *x* 轴的单位向量
是沿着 *x* 轴的单位向量 是沿着 *y* 轴的单位向量
是沿着 *y* 轴的单位向量 是沿着 *z* 轴的单位向量
是沿着 *z* 轴的单位向量
现在,如果您有两个向量 和
和  ,叉积可以通过求解以下行列式得到
,叉积可以通过求解以下行列式得到

有关如何求解行列式的更多信息,请参阅下面的外部链接。
两个向量的叉积、这两个向量的长度以及这两个向量之间的夹角由以下关系给出

从几何上讲,叉积得到一个垂直于这两个参数的向量。请注意对“一个”向量的引用,而不是“该”向量。这是因为有无限多个向量垂直于两个非零向量。叉积的方向可以使用 *右手定则* 来确定:伸出你的右手手指,将你的伸直的手放在第一个向量上,将你的指尖指向与向量相同的方向。将你的手指从第一个向量到第二个向量穿过短角卷曲。你的拇指将指向乘积向量方向。
- 单位向量与自身点积得到 *1*。
- 单位向量与另一个不同的单位向量点积得到 *0*。
按照此顺序排列单位向量: 。从第一个向量开始,移动到第二个向量,然后继续到叉积。如果您首先立即向右移动,则答案为正。如果您首先向左移动,则答案为负。例如
。从第一个向量开始,移动到第二个向量,然后继续到叉积。如果您首先立即向右移动,则答案为正。如果您首先向左移动,则答案为负。例如


给定向量 和标量 r
和标量 r





维基百科上的行列式































