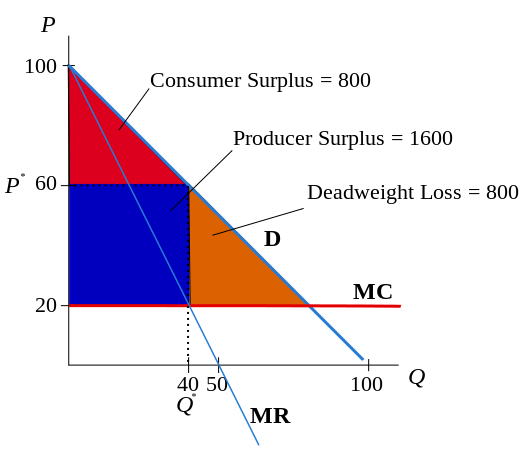信息市场策略/背景/自我评估

测验 #1（自我评估）

问题 #1 和 #2，供求关系

1. 需求由 $Q_{D}=100-P$ 给出。供给由 $Q_{S}=3P$ 给出。绘制供求曲线，并用图形和代数方法求解均衡价格和数量。

用代数方法，我们可以求解这两个数量相等的情况： $Q_{D}=Q_{S}\Rightarrow 100-P^{e}=3P^{e}\Rightarrow P^{e}=25$ 。
然后，均衡数量可以从需求函数或供给函数中得出： $Q_{D}=100-25=75$ 。

2. 假设供给减少，使得 $Q_{S}=3P-24$ 。绘制供给曲线移动情况，并用图形和代数方法求解新的均衡价格和数量。

为了绘制，通过注意到新的供给曲线与旧曲线具有相同的斜率（3，或 1/3 取决于视角）并求解 $Q_{S}=0$ 以找到新的截距在 $P=8$ 。
用代数方法： $Q_{D}=Q_{S}\Rightarrow 100-P^{e}=3P^{e}-24\Rightarrow 4P^{e}=124\Rightarrow P^{e}=31$ 。
$Q_{D}=100-31=69$ .

3. 假设有一个垄断者面临需求 $Q_{D}=100-P$ ，并且生产成本为 $1000+20Q$ 。求边际收益 (MR) 和边际成本 (MC)。绘制垄断者的决策问题，并用图形和数值方法求解利润最大化的数量和价格。

收入只是价格乘以数量，但有一个问题。因为我们想要找到边际收益，也就是数量增加带来的收益变化，我们需要将收入函数表示为数量的函数，而不是价格的函数。因此，第一步是取需求函数 $Q_{D}=100-P$ 并将其转换为逆需求函数 $P=100-Q_{D}$ 。
然后 $R=PQ=(100-Q)Q=100Q-Q^{2}$ 。
边际收益是关于数量的导数： $MR={\frac {dR}{dQ}}=100-2Q$ 。
边际成本类似地是总成本关于数量的导数： $MC={\frac {dC}{dQ}}=20$ 。
用代数方法求解，垄断者在 $MR=MC:100-2Q=20;Q^{*}=40$ 时利润最大化。
为了得到数量为 40，我们回顾反需求函数以找到价格，垄断者设定价格为 $P^{*}=60$ 。

4. 在图表上，确定生产者剩余、消费者剩余和无谓损失。每个是多少？

5. 假设安妮的货币效用（以美元计）由 $U(m)=(m)^{\frac {1}{2}}$ 给出。她对一张彩票的效用是多少，这张彩票以 1/5 的概率支付 100 美元，否则不支付任何东西？

6. 安妮最多愿意为一项赌博支付多少钱，这项赌博以 2/3 的概率支付 36 美元，以 1/3 的概率支付 81 美元？

$U(gamble)=(2/3)36^{\frac {1}{2}}+(1/3)81^{\frac {1}{2}}=(2/3)6+(1/3)9=4+3=7$ .
因此，赌博的效用是 7，但这并非以美元计。7 的效用可以来自各种赌博，或者来自 49 美元的确定性结果 $U(m)=(m)^{\frac {1}{2}}=7\Rightarrow m=7^{2}=49$ 。
对安妮来说，这场赌博价值 49 美元。这被称为赌博的确定性等价物。由于它价值 49 美元，这也是安妮最多愿意为赌博支付的价格。