望远镜制作/项目 1：牛顿反射镜

项目 1：牛顿反射镜

牛顿反射式望远镜是一种极其简单而高效的设计。它由一个镜筒中的两面镜子组成。仅此而已！

牛顿反射镜中的镜子排列和光线路径

较大的曲面镜将入射光线汇聚到焦点。较小的倾斜镜将汇聚的光线从镜筒侧边反射出来，你可以将眼睛放在那里观察图像。在牛顿反射镜中，较小的镜子是平面的，但在相关的卡塞格伦设计中，它是凸面的。阅读维基百科关于牛顿反射镜的文章，了解其历史。

牛顿望远镜 (英文)

在考虑了如何使用望远镜之后，我们将深入研究如何选择这些简单部件的精确形状和尺寸。然后我们将其构建起来！

你将如何使用你的望远镜？

你将如何实际使用你的望远镜？大多数人，包括我自己，都花了很多时间梦想着制作望远镜，却没有认真考虑如何使用它。我谈论了观察星星和行星——但我同时也谈论了观察鸟类和退去的雪原。只有当我透过望远镜观察时，我才发现了一些问题。其中一个问题是，基本的牛顿望远镜会让所有东西看起来都是上下颠倒的！观察星星？这不是问题。观察鸟类或风景？我们遇到了问题。幸运的是，你可以购买一个倒置目镜，它会将物体翻转过来。牛顿望远镜的第二个问题是它天生就非常强大。这意味着你可能正在观察一只鸟的羽毛细节，而不是这只鸟本身。第三，望远镜比一副双筒望远镜大得多，需要支撑才能瞄准它并保持稳定。我不想让你为此感到压力，但你需要考虑，你将用望远镜做什么？

望远镜设计

望远镜设计涵盖了从光学器件（在我们的例子中是两面镜子）到固定这些光学器件并保持其对准的支架，以及包含所有这些器件的镜筒组件。设计还包括支撑框架，该框架固定住镜筒并允许你旋转和指向它。这个部分被称为望远镜架台。

所以，假设你认为你主要想在天空观察行星和恒星。更长的焦距望远镜会提供更高的放大倍率。这就是它的工作原理：焦距越长，你眼睛看到的图像放大倍率就越高。更大的镜子会收集更多光线，但两台焦距相同的镜面尺寸不同的望远镜会在焦点处产生相同大小的图像（尽管由于更大的镜子将更多光线投射到相同大小的图像中，因此具有更大镜子的望远镜中的图像会更亮）。具有较长焦距的镜子在制作起来相对容易，对误差的容忍度也更高。然而，焦距越长，望远镜就越长，使其更难以移动和存放。

较短焦距望远镜提供的放大倍率较低，但视野更广。图像会稍微小一些，但这在透过目镜观察时很少是问题。镜子需要更多工作，不同的技术，但它们与长焦距镜子一样容易制作。较短的望远镜更容易移动，更容易存放，更容易设置使用。

这里没有正确答案。你制作的望远镜应该是一台你感觉舒适且会使用的望远镜。我在过去几年里制作了许多望远镜。我的第一个——我称之为“长狗”——有一个桁架式设计，大约需要五分钟和十颗螺栓才能设置好。桁架杆长六英尺。它很重而且很长，你必须站在梯子上才能够到目镜，但它提供的图像会让你惊叹不已。我在使用这台望远镜时得到了我最喜欢的评论之一。我让一个朋友观看了土星。那是一个完美的夜晚，天空平静，黑暗，土星很高。他看了看这颗行星，说道：“太神奇了，看起来不真实。”这就是我们所说的分辨率。

无论你选择制作多长多大的望远镜，你都会在这里找到构建它的信息。我将为这本书的第一个项目制作两面镜子和几个架台的想法。我将磨制和抛光一面较短焦距的镜子和一面较长焦距的镜子。无论你决定做什么，我都会在这里介绍，你将成功制作你的第一台望远镜。

指向此页面的新术语和主题的链接

• 牛顿望远镜 (英文)

• 桁架式望远镜设计 (英文)

望远镜的各个部分

是时候进入设计的细节了。以下将包含一些基本数学和一些图片来帮助你。

曲率半径

在考虑了望远镜的物理尺寸以及我想用它做什么之后，我现在可以开始考虑光学器件了。焦距取决于在考虑望远镜时做出的选择。焦距由主镜前部的曲率形状决定。我们通过研磨镜子来制作这个曲率。研磨量和曲率深度都直接受到在考虑望远镜时做出的选择的影響。

是镜子的前表面形成图像，因此它是我们关注的焦点。镜子的背面在这个过程中可能会被磨损。这没关系，只要我们没有把它弄裂或在其上造成大的缺口。

望远镜镜面前部的曲率称为曲率半径，缩写为ROC，有时也简称为R。镜子的前部是一个光滑的碗形凹陷。想象一个球，如果你手边有一个，在你阅读时看看它。这个球有一定的半径，从球的中心（一个你无法看到的内部的虚点，但它在那里）到球的内表面。这就是ROC。它定义了球的大小和表面的曲率。

想象一下，球体内部是反光的。再想象一下，我们把一个光源（一种时髦的说法，就是放一个灯泡或手电筒，或者任何能发光的物体）放在球体的中心。所有光线都会反射回中心的光源。然而，如果我们把光源从中心移开，反射点或焦点也会从中心移开，方向相反。当光源离球体中心非常远，达到无穷远时，焦点最终会落在球体中心和球体表面之间大约一半的位置。（“无穷远”究竟有多远？好吧，至少是 ROC 的 200 倍。）

现在想象一下，我们切下球体的一小块，或者把球体表面压入一些柔软的材料中，比如粘土或潮湿的泥土。无论哪种方式，我们都会得到一个浅的、光滑的、碗状的凹陷。它会像望远镜镜面的正面一样弯曲。

镜面的表面具有均匀的曲率，决定着它的焦距。镜子通常是圆形的，它是由那个想象中的球体切下的一个圆形区域。它可以是任何大小，我们将会使用一个几英寸宽的镜子。（作为比较，夏威夷莫纳克亚山上的昴星望远镜的镜面直径为 8.2 *米*，即 27 英尺。）镜面的半径，即其直径的一半，用 *r* 表示。

• 大型望远镜列表 (英语)

主镜

磨入镜面正面的碗状曲线的深度称为 *矢高*。

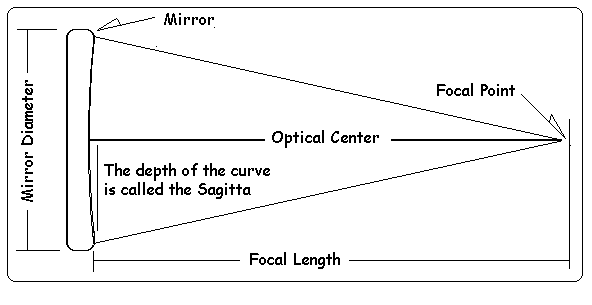
有一个数学公式可以计算出为了达到特定的焦距，矢高应该有多深。

$S={\frac {r^{2}}{2\times ROC}}$

该公式将 ROC 和 *r*（我们知道它是镜面的半径）与 *S*（矢高）联系起来。该公式的意思是，将镜面的半径自乘，然后除以曲率半径的两倍。嗯？好吧，我们可以用尺子或卷尺测量镜面的直径，然后除以二得到镜面的半径。如果它宽 8 英寸，则半径为其一半，即 4 英寸。但是 ROC 是多少呢？

好吧，记住当光源远离球体中心时，焦点是如何移动的。当光源位于无穷远，或远离球体中心很远时，焦点位于球体中心和球体表面之间的中点。因此，焦距是曲率半径的一半，即 ROC 的一半。

这时，我们必须针对望远镜进行具体说明：你想要什么焦距？嗯，你想要多长的望远镜？假设你想要一个四英尺长的望远镜。ROC 是这个长度的两倍，即 8 英尺。（如果你之前制作过望远镜，你可能现在正在气愤，因为你知道望远镜的长度与镜面的焦距几乎没有关系。我会在最后解释清楚。）

我问，为什么我计算 ROC，而它只是焦距两倍的另一种说法？为什么不在矢高公式中直接使用焦距呢？ROC 的两倍等于焦距的四倍，那么为什么不使用这个呢？

$S={\frac {r^{2}}{4\times f}}$

好吧，你可以这样做。对于我们业余爱好者来说，我们可以使用其中任何一个，效果都足够好。

所以！让我们计算一个直径为 8 英寸，焦距为 48 英寸的镜面的矢高。

直径为 8 英寸，焦距为 48 英寸的镜面的矢高计算

$S={\frac {r^{2}}{4\times f}}={\frac {4^{2}}{4\times 48}}={\frac {16}{192}}=0.08333$

不多吧？0.08333 英寸（而且这三个数字会无限循环下去）。它大约相当于一个（美国）便士的厚度。一令纸的厚度接近 2 英寸。一令纸包含 500 张。250 张乘以 0.08333 大约等于 21 张。

你需要多精确？你想要多么接近四英尺的望远镜？镜面的焦距会在一定程度上决定望远镜筒的长度，为了简单起见，你可以假设镜面的焦距和望远镜筒的长度相同。*但是*请注意，在实际操作中，望远镜筒的长度会比实际焦距长 25%。如果五英尺的望远镜听起来太大了，你可以重新计算一个 3 英尺的焦距，或者任何你想要的其他值。

我们已经花了几个段落讨论主镜，我只分享了一些基础知识。许多优秀的书籍和网页都记录了主镜的制作过程。请查看本书末尾的链接。现在我们需要考虑光学系统的另一半，即副镜。

副镜

在上图（以及维基百科关于牛顿望远镜的页面）中，我们看到望远镜收集和聚焦光线，将光线反弹回望远镜筒。然后，光路转弯 90 度，焦点和目镜位于望远镜筒的一侧。这是通过在望远镜筒中以 45 度角放置一块平面镜来实现的。（在小型望远镜中，可以使用棱镜，但对于我们来说，镜子更简单，制作起来也更容易，效果也一样好。）

• 阿米西屋顶棱镜 (英语)

这个 *副镜* 的大小，它的形状，以及它相对于主镜的位置，都是望远镜基本尺寸的函数。在上一节中，我们以一个焦距为 48 英寸、直径为 8 英寸的镜子为例进行计算。在本节中，我将继续使用这个例子。

副镜通常呈椭圆形。它们以短轴表示。一个 1 英寸的副镜，其宽度为 1 英寸，长度约为 2 英寸，呈椭圆形。你可以使用一个长宽大致相同的矩形镜子，它也能很好地工作。如果你拿着一面这样的镜子，并绕着它的短轴旋转，使其与你的视线成 45 度角，它会缩短，看起来是圆形或方形，具体取决于镜子的形状。

调整望远镜筒的大小

在我们计算副镜的大小和位置之前，我们需要考虑支撑镜面的望远镜筒。它应该有多长？直径多大？主镜要安装多深？

如果我们只将望远镜筒的大小调整为主镜的直径，那么将镜子安装在望远镜筒中就会很困难。此外，镜面的一部分表面会被浪费。镜面的外边缘会被望远镜筒壁遮挡，图像会受到反射和衍射的影响，即光线被望远镜筒壁弯曲和散射。这会导致图像周围出现许多未聚焦的光线，并降低分辨率。在镜子和望远镜筒壁之间增加空间可以减少这种影响。

镜筒需要比主镜大，大多少？安全的数字是主镜周围留出1英寸的间隙。这样算下来，镜筒的直径要比主镜大2英寸。以我们示例中的8英寸主镜为例，镜筒的直径应为10英寸。

镜筒长度由主镜的焦距决定，再加上主镜和镜架（即支撑主镜并使其垂直于镜筒轴线的框架）末端的空间。

典型的主镜和镜架堆叠起来的高度约为3到4英寸。将此高度加到焦距上，您将得到一个足够长的镜筒（记住，焦距的一部分被副镜横向转向）。再增加一点长度，比如3到4英寸，就可以形成一个遮挡杂散局部光的遮光板。我们示例中的主镜焦距为48英寸。再加4英寸用于主镜和镜架，再加4英寸用于遮挡光线，我们得到了一个长度为56英寸，直径至少为10英寸的镜筒。

• 暗角 (中文)

副镜尺寸

那么，我们要把副镜做多大呢？在我们回答这个问题之前，需要考虑另一个关键尺寸，即焦距偏移。

偏移是指从副镜中心（实际上是镜筒中心）到图像焦点的距离。将其视为镜筒半径（镜筒直径的一半）加上调焦器完全拉出时的高度。我使用3英寸来表示这个数字，因为我没有购买调焦器。因此，我们示例望远镜的偏移为5英寸加上3英寸，即8英寸。

计算副镜尺寸的公式如下。

$d={\frac {Os\times D}{f}}$

在这个公式中，

• Os 是焦距偏移，
• D 是主镜直径，
• f 是主镜焦距，
• d 是副镜小轴直径。

我们将主镜直径乘以焦距偏移，然后除以主镜焦距。这将给我们一个最小的小轴尺寸。第二个经验法则就是，副镜的尺寸不应超过主镜直径的20%。对于一个8英寸的主镜，这个尺寸是1.6英寸。纯粹主义者会永远争论这些数字。我的意见和经验是，一个稍微偏大的副镜比一个稍微偏小的副镜更好。

让我们看看这个公式是如何工作的。我使用了这些值

$d={\frac {Os\times D}{fl}}={\frac {8\times 8}{48}}={\frac {64}{48}}=1.333$

这个公式得出1.33英寸的尺寸。这是最小尺寸。您可以将它增加25%，得到一个更好的副镜尺寸。1.33 x 1.25 = 1.66英寸，这正好是20%的标记。很酷吧？

就是这样！从主镜的直径和焦距开始，我们就可以确定镜筒的直径和长度，以及副镜的尺寸。

这些公式非常重要，我已经将它们包含在一个可以制作成3 x 5卡片的图形中。打印出来吧！

矢高计算/曲率深度

$S={\frac {r^{2}}{4f}}$

S = 矢高

r = 主镜半径

f = 主镜焦距

副镜尺寸/小轴公式

$r={\frac {Os\times D}{f}}$

r = 副镜小半径

Os = 偏移

D = 主镜直径

f = 主镜焦距

这些公式以及导致它们的考虑因素将指导您的第二台望远镜以及您在此之后制作的每一台望远镜。但接下来您需要教您的双手如何研磨和抛光镜面，而这最好是在简单且廉价的材料上学习。