金融科学/概率与风险评估

经济学中的概率

要赋予概率以客观意义，有必要且唯一必须的是它可以被测量。为此，有必要且唯一必须的是实验可以被重复。通过多次重复相同的实验，其结果的概率可以通过其出现频率来测量。但在经济学中，实验永远无法重复。每个经济事件都是独一无二的。所有主体总是不一样，他们所处的条件也永远不会完全相同。因此，经济概率不可能具有客观意义。但是，概率模型对经济学至关重要。错误在哪里？经济学中的概率模型是否总是错误的，因为经济学中的概率没有客观意义？

只要不作弊，机会游戏的偶然性可以被认为是纯粹的概率性，因为它们通常是可重复的实验。经济不确定性不是严格的概率性，但关于风险的经济决策非常类似于赌徒的决策。当我们面对风险时，我们就像在与现实打赌一样进行推理。当我们将概率归因于预期的经济事件时，它们永远不可能是真实和准确的，但它们仍然可以是做出更好决定的估计。例如，保险公司必须估计死亡概率。它根据记录的死亡人数的统计数据来做到这一点。如果它不这样做，它将无法预测其支付义务，并面临破产风险。

经济学中的概率模型永远不可能完全正确，但它们可能与现实足够相似，以至于值得比较。所有需要的就是一个相关的类比来证明模型。即使模型非常错误，它们也可能有用，因为模型与现实之间的差距可能非常大。

风险的衡量

风险通常被称为可衡量的量：在确定性情况下，风险为零，随着不确定性的增加而增加。标准差与项目平均利润之比通常是其风险的一个很好的度量，因为它随着不确定性的增加而增加，并且因为它可以比较具有不同平均利润的项目。但是，单个量永远无法足以解释各种风险。标准差衡量的是概率分布的离散程度，但这种分布的形状对于评估风险也很重要。它决定了非常高和中等收益以及中等和非常高损失之间的概率分布。标准差衡量的是离散程度，但它没有说明形式的多样性。因此，它特别适用于比较具有相同形式的分布。例如，如果两个分布是正态（高斯）的，那么显然具有最大标准差的分布风险最大。但是，如果分布具有不同的形式，比较它们的标准差不一定是一种比较它们风险的好方法。此外，标准差并不是衡量分布离散程度的唯一量。平均值的绝对值偏差的平均值有时比平均值的平方偏差的均方根更自然地估计离散程度，而平均值的平方偏差的均方根则非常重视大型差异，而损害小型差异。

当我们测量分布的离散程度时，我们在获胜的概率（当回报高于其平均值时）和亏损的概率（当回报低于其平均值时）上进行平均。当人们质疑公司或项目的生存能力时，亏损的风险尤其重要。我们特别关注概率分布的左侧，而右侧的离散程度（获胜的概率）不会给我们任何信息。

风险价值 (Value at Risk)，是广泛用于研究公司生存能力的亏损风险指标。

随机变量 $X$ 的 p 风险价值，根据定义，是指这样的数字 $V_{X}^{R}(p)$，使得 $Pr(X\leq -V_{X}^{R}(p))=p$。 $X$ 的正值为利润，负值为亏损。

$Pr(X\leq x)=F_{X}(x)$ 表示 $X\leq x$ 的概率。 $F_{X}$ 是随机变量 $X$ 的累积分布函数。 $F_{X}(x)=\int _{-\infty }^{x}f_{X}(y)dy$ 其中 $f_{X}$ 是 $X$ 的概率密度函数。

$V_{X}^{R}(p)=-F_{X}^{-1}(p)$

风险价值使我们能够估计可能发生的损失。我们知道，以 $1-p$ 的概率，损失不会超过 $V_{X}^{R}(p)$。 $p$ 通常是一个很小的数字，例如 $0.05=5\%$ 或更小。概率低于 $p$ 的损失可以被认为是异常损失。风险价值用于估计最大普通损失，但它不能说明异常损失。如果损失的概率低于 $p$，它们对 $V_{X}^{R}(p)$ 没有影响。两家公司，其中一家面临着巨大但罕见的损失，而另一家则没有，它们可能具有相同的风险价值。

标准差、平均绝对偏差或风险价值等风险指标永远无法提供面对风险的完整信息。为了完全了解风险，必须了解预期收益和损失的概率密度函数，或者等效地，了解它们的累积分布函数。

风险的价格

一般而言，人们认为风险会降低项目的价值。低利润尤其是损失的风险通常会让人望而却步，即使高利润的可能性使平均利润相当可观。在两个平均利润相同的项目中，风险较高的项目通常价值较低。这种价值下降是一种风险溢价。为了让一个有风险的项目具有吸引力，它通常必须比无风险利率产生更高的收益，它必须有足够的平均利润来抵消风险承担。风险溢价可以从抵消风险所需的超额利润率计算得出，即所需利润率与无风险利率之间的差额。

风险厌恶并非普遍现象。有很多例外。风险可能不会降低项目的价值，反而会让人们主动寻求它。例如，在大多数机会游戏中，人们总是平均输钱，平均利润为负，但即使是极小的获利可能性也能说服赌徒参与。他们赋予寻求的风险的价值抵消了他们的平均损失。

由于经济主体面对风险的态度并不相同，他们对风险的评估也大相径庭。这促进了风险交易。对一个主体来说非常令人却步的风险，对另一个主体来说可能微不足道。第二个主体有兴趣向第一个主体出售风险保障。

不确定项目的折现

风险调整贴现率有时被定义为在无风险贴现率的基础上加上风险溢价，风险溢价衡量的是风险带来的额外收益。但是，对于计算一个不确定项目净现值而言，这种定义只有在项目只有一次初始成本和一次最终收益时才成立。如果存在不确定的损失，用高于无风险利率的贴现率对损失进行折现显然是愚蠢的。当不确定的支付在一段时间内分期进行时，通常没有理由用相同的风险调整贴现率对其进行折现，因为它们可能具有非常不同的不确定性。

贴现率就是无风险利率。它是由被认为安全的投资利率估计得到的，但这并不妨碍将其应用于不确定项目的评估。它是今天支付的资金与以后支付的资金之间的汇率，是一种时间汇率。一个项目是确定且无风险的，还是非常不确定且非常冒险，不应该改变支付贴现的方式。为了评估风险项目，所有收入和成本都必须以无风险投资利率进行折现，因为这是将分期支付的资金加总在一起的最佳方式。这些支付是否以确定性预测得到并不影响情况。贴现率取决于特定时刻的经济现实，而不是它被应用于的项目。对于面对相同现实的所有项目，无论它们是否有风险，贴现率都是相同的。

如果一个项目有风险，并且收入和成本的概率已知，我们可以用真实贴现率（而不是风险调整利率）计算收入、垫付现金和其他成本的平均折现值，因此可以计算出平均利润、平均利润率和平均净现值。但这并不是项目的净现值，因为它没有考虑风险溢价。

一个不确定项目的净现值是其平均净现值减去风险溢价。风险溢价是抵消风险所需的平均超额利润的现值。它是平均所需利润与将资金投资于无风险利率所能获得的利润之间的差额的现值。由于平均净现值是平均超额利润的现值，因此不确定项目的净现值是平均超额利润与抵消风险所需的超额利润之间的差额的现值，因此也是平均利润与抵消风险所需的利润之间的差额的现值。

统计独立、反相关和风险降低

有两种技术可以降低风险。一种利用经济事件的统计独立性，另一种利用它们的负相关性。

• 当许多项目在统计上独立时，它们的总和比每个单独的项目风险要低得多。一个简单的例子就足以让人信服：如果 $n$ 个统计独立的项目具有相同的预期平均利润 $\pi$ 和相同的标准差 $\sigma$，$\sigma /\pi$ 衡量的是单个项目的风险。它们的总和的预期平均利润为 $n\pi$，标准差为 $\sigma {\sqrt {n}}$，因为独立变量之和的方差是它们的方差之和。因此，所有项目之和的风险用 ${\frac {\sigma {\sqrt {n}}}{n\pi }}={\frac {\sigma }{\pi {\sqrt {n}}}}$ 来衡量，当 $n$ 非常大时，它接近于零。总的来说，项目不一定具有相同的预期平均利润或相同的风险，但如果它们在统计上是独立的，它们的总和的风险通常远低于单独考虑的每个项目的风险，并且当项目数量非常大时，风险接近于零。

• 当一个项目的成功与另一个项目的失败相关联时，这两个项目是反相关的，或负相关的。它们的利润协方差为负。例如，股票价格的上涨与该股票看跌期权价值的下降相关联。资产和对应期权价值之间的正相关和负相关会导致无风险投资组合，这些投资组合构成了 Merton、Black 和 Scholes 在后面提出的期权定价方法的基础。正相关可以通过做空来利用，可以通过卖空、买入看跌期权或卖出看涨期权来实现。卖空是指卖出借来的股票，并承诺稍后买回归还。风险对冲策略通常涉及同时对某些资产的升值和对其他资产的贬值进行押注。但是，资产通常是正相关的，它们的价值往往同时上涨或下跌。因此，一些资产的上涨通常与其他资产的下跌反相关。因此，对冲策略降低了与资产价值变化相关的风险。人们试图在市场上涨和下跌时都能获利。

赌场经济

一个项目通常受到许多不确定事件的影响，这些事件会增加或减少其利润。必须区分两种类型的事件，一种只影响项目当前利润，例如意外成本或收入，这些成本或收入会暂时影响项目的利润，但不会影响其未来利润；另一种事件会永久影响项目获利能力。第一类事件的影响必须加起来以获得其累积效应，而第二类事件的影响必须相乘。

假设一个项目只受第二类事件的影响：许多随机事件 $i$ 可以在时间间隔 $dt$ 内影响其价值 $V$。每个事件 $i$ 如果发生，会将 $V$ 乘以一个因子 $R_{i}>1$，如果它促进了项目的成功，而如果它不利，则乘以 $<1$。我们假设事件 $i$ 的概率为 $p_{i}=\rho _{i}dt$，并且它们是独立的。然后，$\ln V$ 的变化是随机变化 $\ln R_{i}$ 的总和。根据中心极限定理，如果这些变化非常多，与它们的总和相比很小并且独立，则该总和的概率分布为正态分布。设 $\mu dt$ 是它的平均值，$\sigma ^{2}dt$ 是它的方差。如果项目环境是恒定的，$\mu$ 和 $\sigma$ 不依赖于 $t$。在时间 $T$ 上，$\ln V$ 的变化服从平均值为 $\mu T$，方差为 $\sigma ^{2}T$ 的正态分布。

设项目的初始值为 $V_{0}$。由于 $\ln V$ 服从均值为 $\ln V_{0}+\mu T$、方差为 $\sigma ^{2}T$ 的正态分布，则 $V$ 服从对数正态分布，其概率密度为

$f(V)={\frac {1}{V\sigma {\sqrt {t}}{\sqrt {2\pi }}}}e^{-(\ln {\frac {V}{V_{0}}}-\mu T)^{2}/2T\sigma ^{2}}$

$V$ 的平均值为 $V_{0}e^{(\mu +\sigma ^{2}/2)T}$，其标准差为 $V_{0}e^{(\mu +\sigma ^{2}/2)T}{\sqrt {e^{\sigma ^{2}T}-1}}$。如果我们用标准差与均值的比率来衡量风险，我们得到 ${\sqrt {e^{\sigma ^{2}T}-1}}$，它随着 $T$ 的增加而迅速增长。

Suppose now that a project is affected only by events of the first type. Many random events $i$ can influence the current profit $d\Pi$ during a time interval $dt$. Each event $i$ if it occurs increases $d\Pi$ by an amount $d\Pi _{i}>0$ if it is a receipt and $<0$ if it is a cost. We assume that the events $i$ have probabilities $p_{i}=\ rho_{i}dt$ and that they are independent. The current profit $d\Pi$ during $dt$ is then a sum of random variations $d\Pi _{i}$. According to the central limit theorem, if these variations are very numerous, small compared to their sum and independent, the distribution of probabilities of this sum $d\Pi =\sum _{i}d\Pi _{i}$ is a normal law. Let $\mu dt$ be its mean and $\sigma ^{2}dt$ its variance. If the project environment is constant, $\mu$ and $\sigma$ do not depend on $t$. On a duration $T$, the profit $\Pi$ follows a normal distribution with mean $\mu T$ and variance $\sigma ^{2}T$. The ratio of the standard deviation on the average is ${\frac {\sigma }{\mu {\sqrt {T}}}}$ and approaches zero when $T$ is large.

在较长的时间段内，由第二类事件引起的风险往往会超过由第一类事件引起的风险。因此，为了评估风险，我们通常可以忽略第一类事件，从而保留对数正态分布。但这条规则并非普遍适用。如果与第一类事件相关的风险很重要，则不应忽略它们，尤其是当考虑的时间较短时。

所有证明 $\Pi$ 的正态分布或 $V$ 的对数正态分布的先验假设都非常值得怀疑。 $d\Pi _{i}$ 和 $\ln R_{i}$ 不一定比它们的总和小得多，因为单个事件可能对项目的成功或失败产生重大影响。它们也不一定相互独立，因为失败可能导致更多失败或更多成功，或者失败可能在成功之前通过韧性而出现，或者成功可能导致失败，因为伟大有时先于衰落。此外，通常没有理由假设概率 $p_{i}=\rho _{i}dt$ 随着时间推移而保持不变，因为经济事件取决于不断变化的环境。事实上，通常没有理由可以正确定义这些概率，因为经济事件永远不可能完全复制。真实的经济可能与赌场经济有很大不同。这只是一个数学模型，可以帮助我们理解现实，但也可能误导我们。

对于对数正态分布，标准差与均值的比率 ${\sqrt {e^{\sigma ^{2}T}-1}}$ 不一定是一个好的风险指标，特别是当分布非常扁平化时，对于 $\sigma ^{2}T>1$ 的值。一般来说，人们更喜欢 $\sigma {\sqrt {T}}$，这也是预期值围绕均值分散的一个指标。 $\sigma {\sqrt {T}}$ 是对数收益的标准差。它被称为波动率。如果时间以年为单位，$\sigma$ 就是年波动率。

在本节中，我们对项目价值进行了推理，但我们本可以对股票市场的价格保持相同的推理。在这种情况下，对数正态分布是一个相当好的近似值，但它略微低估了与平均值大幅度偏差的概率（Luenberger 1997）。

为了更容易推理，我们在以下内容中将做出一些简化的假设。

• 股票价格变化始终由对数正态分布表示，其参数 $\mu$ 和 $\sigma$ 不变。

• 我们对不支付股利的股票进行推理。因此，利润仅为资本收益。这相当于假设已支付的股利被系统地再投资。

• 忽略通货膨胀。这意味着我们对实际价值进行推理，而不是对名义价值进行推理。

• 忽略交易成本和税收。

• 我们假设存在一个单一的无风险利率。因此，我们忽略了它的期限结构。最重要的是，我们忽略了即使“无风险”利率也是有风险的，因为即使没有借款人违约的风险，也总是存在通货膨胀的风险。

这些简化的假设使得能够将推理集中在一些最重要的点上，但如果我们想将结论应用于现实世界，我们当然必须意识到理论忽略的复杂情况。

算术收益率、对数收益率和平均收益率

算术收益率，或简称为收益率，是资产的利润率。如果 $V_{i}$ 是其初始价值，而 $V_{f}$ 是其最终价值，则利润为 $V_{f}-V_{i}$，利润率为 $r={\frac {V_{f}-V_{i}}{V_{i}}}$，因此 $V_{f}=V_{i}(1+r)$

对数收益率为 $R=\ln({\frac {V_{f}}{V_{i}}})=\ln(1+r)$，因此 $V_{f}=V_{i}e^{R}$

当 $r\ll 1$，$R\approx r$

当需要将收益率进行逐期叠加时，使用对数收益率比使用算术收益率更方便

$r_{12}=(1+r_{1})(1+r_{2})-1=r_{1}+r_{2}+r_{1}r_{2}$

而

$R_{12}=\ln(e^{R_{1}}e^{R_{2}})=R_{1}+R_{2}$

在计算投资组合收益率时，使用算术收益率比使用对数收益率更方便

$r_{pf}={\frac {\sum _{n=1}^{N}V_{ni}r_{n}}{\sum _{n=1}^{N}V_{ni}}}=\sum _{n=1}^{N}\omega _{n}r_{n}$

其中，$V_{ni}$ 是组成投资组合的 $N$ 种资产的初始值，$r_{n}$ 是它们各自的收益率。 $\omega _{n}$ 是资产 $n$ 在投资组合中的权重。

$R_{pf}=\ln(1+r_{pf})\neq \sum _{n=1}^{N}\omega _{n}R_{n}$

当 $R$ 是一个随机变量时，对数收益率的平均值并不等于由平均收益率计算的对数收益率，这就是为什么对数平均收益率 $R_{m}$ 的定义不是对数收益率的平均值，而是平均最终值与初始值之比的对数

$R_{m}=\ln({\frac {\langle V_{f}\rangle }{V_{i}}})\neq \langle R\rangle$

如果 ${\frac {V_{f}}{V_{i}}}$ 服从对数正态分布，参数为 $\mu$ 和 $\sigma$，则对数平均收益率为 $\mu +\sigma ^{2}/2$，因为 $e^{\mu +\sigma ^{2}/2}=\langle {\frac {V_{f}}{V_{i}}}\rangle ={\frac {\langle V_{f}\rangle }{V_{i}}}$，但对数收益率的平均值为 $\mu$，因为 $\ln({\frac {V_{f}}{V_{i}}})$ 服从均值为 $\mu$ 的正态分布。对数收益率的标准差为 $\sigma$。它衡量的是对数收益率围绕其均值 $\mu$ 的离散程度，而不是围绕对数平均收益率 $\mu +\sigma ^{2}/2$ 的离散程度，但二者之间的差异通常很小。对于一个风险资产 $\mu =0.1$ 和 $\sigma =0.15$ 是年度对数收益率的典型值，而 $\mu +\sigma ^{2}/2\approx 0.11$

资产预期价值的演变

假设资产价格变化是随机的，并且可以用上述对数正态分布来描述。

如果 $V_{0}$ 是资产的现值，其在日期 $T$ 的未来值 $V_{T}$ 服从对数正态概率密度分布 

$f(V)={\frac {1}{V\sigma {\sqrt {T}}{\sqrt {2\pi }}}}e^{-(\ln V-\ln V_{0}-\mu T)^{2}/2T\sigma ^{2}}$

未来价格的平均值或期望值是

$\langle V_{T}\rangle =e^{\ln V_{0}+\mu T+\sigma ^{2}T/2}=V_{0}e^{(\mu +\sigma ^{2}/2)T}$

资本资产定价模型

资本资产定价模型 (CAPM) 是一个简化的模型，它展示了理想化的金融市场如何评估风险溢价。该模型的主要结论是，风险溢价不取决于资产价值的标准差，而取决于其与一般经济状况的协方差。这衡量了不可消除的风险，而标准差则包括可以通过多元化消除的风险。

如果所有经济项目在统计学上都是独立的，我们可以始终通过多元化来消除它们的风险。一个共同基金可以从大量风险资产中构建一个几乎无风险的投资组合。由于风险几乎被消除，其成本将微不足道，风险溢价也将几乎为零。只要所有风险项目的收益率至少与无风险利率相同，它们就将具有吸引力。但经济项目通常并非独立的。相反，它们通常依赖于相同的经济条件，因为所有参与者都对总体繁荣或萧条敏感，因此它们通常相互关联。通过多元化并不总是能够消除风险。无法消除风险的风险项目必须具有更高的平均收益率。资本资产定价模型衡量了不可消除的风险以及它们产生的风险溢价。它基于一些简化的假设

• 参与者始终根据其平均收益率衡量投资组合的绩效，并根据该收益率的标准差衡量风险。他们都对平均资产收益率、标准差和协方差有相同的信息。

• 他们可以自由地以无风险利率借贷，且无需成本。

• 他们可以始终构建多元化投资组合。所有资产的加权和都是潜在的投资组合。

最优投资组合的半直线

设 $r_{m}$ 是高于无风险利率 $r_{f}$ 的收益率（算术，而非对数）。设 $\Omega (r_{m})$ 是所有具有相同平均收益率的风险投资组合的集合。设 $\sigma _{min}(r_{m})$ 是 $\Omega (r_{m})$ 中最优投资组合收益率的标准差：对于 $\Omega (r_{m})$ 中的任何投资组合，其收益率的标准差大于或等于 $\sigma _{min}(r_{m})$。那么，在 $\sigma r$ 半平面中的最优投资组合的半直线由以下公式给出

$r=r_{f}+(r_{m}-r_{f}){\frac {\sigma }{\sigma _{min}(r_{m})}}$

所有可能的投资组合的$(\sigma ,r)$ 都位于这条半直线的下方。半直线上的所有点都是最佳的$(\sigma ,r)$ 投资组合。对于给定的预期收益，它们是风险最低的；而对于给定的风险，它们是最有利可图的。

证明：我们先证明半直线上的所有点都是可能的投资组合。考虑一个投资组合，它由$\alpha$ 无风险利率和$(1-\alpha )$ 最佳投资组合组成，该最佳投资组合的利率为$r_{m}$。它的平均收益是$\alpha r_{f}+(1-\alpha )r_{m}$，该收益的标准差是$(1-\alpha )\sigma _{min}(r_{m})$，因此它位于最佳投资组合的半直线上。如果$0\leq \alpha \leq 1$，$r$ 在$r_{f}$ 和$r_{m}$ 之间。如果$\alpha <0$，$r>r_{m}$。在这种情况下，投资者以无风险利率$r_{f}$ 借款，然后以风险利率$r_{m}$ 进行投资，并通过杠杆作用提高平均收益。

令$(\sigma ,r)$ 为最佳投资组合半直线上方的一点，并假设它代表一个可能的投资组合。与上面相同的论证，从$(0,r_{f})$ 出发，并经过$(\sigma ,r)$ 的半直线，也代表可能的投资组合。特别是$(\sigma {\frac {r_{m}-r_{f}}{r-r_{f}}},r_{m})$ 将代表一个可能的投资组合。由于$(\sigma ,r)$ 位于最佳投资组合半直线上方

${\frac {r-r_{f}}{\sigma }}>{\frac {r_{m}-r_{f}}{\sigma _{min}(r_{m})}}$

因此

$\sigma _{min}(r_{m})>\sigma {\frac {r_{m}-r_{f}}{r-r_{f}}}$

但这与 $\sigma _{min}(r_{m})$ 的定义相矛盾，它是相同收益 $r_{m}$ 的所有可能投资组合的标准差中的最小值。所以，如果 $(\sigma ,r)$ 在最佳投资组合的半直线之上，它不能代表一个可能的投资组合。

可以得出结论，

${\frac {\sigma _{min}(r_{m})}{\sigma _{min}(r_{M})}}={\frac {r_{m}-r_{f}}{r_{M}-r_{f}}}$

对于所有大于 $r_{f}$ 的 $r_{m}$ 和 $r_{M}$，因为 $(\sigma _{min}(r_{m}),r_{m})$ 和 $(\sigma _{min}(r_{M}),r_{M})$ 都位于最佳投资组合的半直线上。

最优市场假设

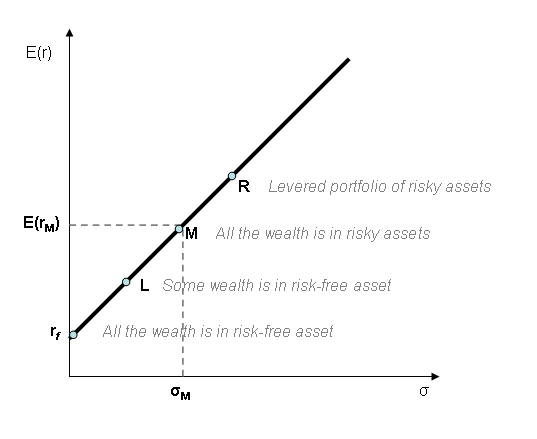
市场组合原则上包含一个经济体中可以交易的所有资产，无论是有风险的还是无风险的。它包括所有可以带来利润的财富，无论是证券还是房地产，只要它们有市场价格。它的平均收益取决于经济的繁荣程度。它的标准差代表了所有主体面临的总体风险，因为它代表了经济普遍不景气的风险。由于市场组合是最多样化的，它消除了所有可以通过多元化消除的风险。高度多元化的投资组合，如 SP500，也消除了可以通过多元化消除的风险。

最优市场假设认为市场组合位于最佳投资组合的半直线上。

该假设显然是错误的，因为主体在投资时并不总是理性的。但作为第一近似，我们可以假设像 SP500 这样的高度多元化的投资组合与最优投资组合没有太大区别。然后，我们通过估计 SP500 或其他精心挑选的、高度多元化的投资组合的平均收益及其标准差来确定最佳投资组合的半直线。

与一般经济状况的协方差

如果我们假设市场组合是最佳的，并且如果$r_{M}$ 是其平均收益率，$\sigma _{min}(r_{M})$ 是其收益率的标准差 $\sigma _{M}$。

资产 $i$ 的 $\beta _{i}$ 根据定义是

$\beta _{i}={\frac {Cov(x_{i},x_{M})}{\sigma _{M}^{2}}}$

其中 $x_{i}$ 和 $x_{M}$ 分别是资产 $i$ 和市场组合的随机收益率。

$\beta _{i}$ 与市场组合收益率的协方差成正比，因此与一般经济状况成正比。

我们将证明

$\beta _{i}={\frac {r_{i}-r_{f}}{r_{M}-r_{f}}}$

其中 $r_{i}$ 是资产 $i$ 的平均收益率。

考虑一个包含资产 $i$ 的价值 $\alpha$ 和最佳投资组合的 $(1-\alpha )$ 的投资组合，该投资组合具有相同的平均收益 $r_{i}$。该投资组合的收益率为 $r_{i}$。设 $v(\alpha )$ 为其收益率的方差。由于 $v(\alpha )$ 在 $\alpha =0$ 时最小，${\frac {dv}{d\alpha }}(0)=0$。

设 $x_{i}$ 为资产 $i$ 的随机收益，$x_{opt}$ 为具有相同平均收益的最佳投资组合的随机收益。

$r_{i}=E(x_{i})=E(x_{opt})$

${\frac {dv}{d\alpha }}={\frac {d}{d\alpha }}[\alpha ^{2}\sigma _{i}^{2}+2\alpha (1-\alpha )cov(x_{i},x_{opt})+(1-\alpha )^{2}\sigma _{opt}^{2}]$

$=2\alpha \sigma _{i}^{2}+2(1-2\alpha )cov(x_{i},x_{opt})+(2\alpha -2)\sigma _{opt}^{2}$

${\frac {dv}{d\alpha }}(0)=2Cov(x_{i},x_{opt})-2\sigma _{opt}^{2}=0$

因此

$Cov(x_{i},x_{opt})=\sigma _{opt}^{2}=\sigma _{min}(r_{i})^{2}$

收益率为$x_{opt}$ 的投资组合可以由市场投资组合的${\frac {r_{i}-r_{f}}{r_{M}-r_{f}}}=\beta _{i}'$ 和无风险资产的${\frac {r_{M}-r_{i}}{r_{M}-r_{f}}}=(1-\beta _{i}')$ 组成。所以

$Cov(x_{i},x_{opt})=\beta _{i}'Cov(x_{i},x_{M})$

现在

$Cov(x_{i},x_{opt})=\sigma _{min}(r_{i})^{2}=\beta _{i}'^{2}\sigma _{M}^{2}$

因此

$\beta _{i}'={\frac {Cov(x_{i},x_{M})}{\sigma _{M}^{2}}}=\beta _{i}$

$\beta$ 度量的是通过多元化无法消除的风险

我们定义随机变量 $\epsilon _{i}$ 为

$x_{i}=r_{f}+\beta _{i}(x_{M}-r_{f})+\epsilon _{i}$

那么

$E(\epsilon _{i})=E(x_{i})-\beta _{i}E(x_{M}-r_{f})-r_{f}=0$

$Cov(\epsilon _{i},x_{M})=Cov(x_{i}-\beta _{i}x_{M}-(1-\beta _{i})r_{f},x_{M})=Cov(x_{i},x_{M})-\beta _{i}Cov(x_{M},x_{M})=Cov(x_{i},x_{M})-\beta _{i}\sigma _{M}^{2}=0$

$\sigma _{i}^{2}=\beta _{i}^{2}\sigma _{M}^{2}+\sigma _{\epsilon _{i}}^{2}$

$x_{i}$ 的方差是两项之和。 $\beta _{i}^{2}\sigma _{M}^{2}$ 代表一种无法通过多元化消除的风险。 $\sigma _{\epsilon _{i}}^{2}$ 代表可以通過多元化消除的风险，因为它是与市场组合不相关的随机变量的方差。

风险溢价仅取决于与一般经济状况的协方差。

资产 $i$ 的风险溢价是抵消其风险所需的超额利润的现值。它从所需的超额利润率 $r_{i}-r_{f}$ 获得。由于 $r_{i}-r_{f}=\beta _{i}(r_{M}-r_{f})$，资产 $i$ 的风险溢价仅取决于 $\beta _{i}$，因此仅取决于与一般经济状况的协方差。

如果 $\beta _{i}=0$，资产 $i$ 的风险溢价为零。可能这种资产风险也很高，具有很高的 $\sigma _{i}$，但是这种风险可以通过与其他资产的组合来消除，这些资产的 $\beta$ 为零。这就是风险溢价为零的原因。

当 $\beta$ 为负数时

如果 $\beta _{i}$ 为负数，$r_{i}=r_{f}+\beta _{i}(r_{M}-r_{f})<r_{f}$。为什么当它平均而言带来低于无风险收益的收益或亏损时，我们还要同意持有风险资产 $i$ 呢？

一个投资组合的 $\beta$ 是其组成资产 $j$ 的 $\beta _{j}$ 的加权平均值，因为一组随机变量与其自身的协方差之和等于它们分别与该变量的协方差之和。一个 $\beta _{i}$ 为负数的资产 $i$ 会降低包含它的投资组合的 $\beta$，因此降低了无法通过多元化消除的风险。收益的下降被风险的下降所抵消。

如果标的资产的 $\beta$ 为正数，看跌期权就是一种负 $\beta$ 资产，因为看跌期权与标的资产负相关。看跌期权的 $\beta$ 甚至可以足够负数以至于平均收益为负数。这种期权的购买价格比其平均收益更高。那么为什么还要买看跌期权？因为它们可以降低一个没有它们就会非常冒险的投资组合的风险。

三种风险

• 如果 $\beta _{i}>0$，资产 $i$ 的风险与市场正相关。这种风险无法在不降低收益的情况下消除。
• 如果 $\beta _{i}=0$，资产 $i$ 的风险与市场无关，可以通过多元化在不降低收益的情况下消除。
• 如果 $\beta _{i}<0$，则资产 $i$ 的风险与市场负相关。 $i$ 与市场的反相关性降低了投资组合的风险，该投资组合的 $\beta$ 为正，同时降低了投资组合的收益。

投资组合优化

即使放弃了有效市场假说，CAPM 仍然可以使用，因为它提供了一种优化投资组合的方法。

首先选择一个合理的投资组合，例如标普 500 指数，然后开始估计其平均收益 $r_{I}$ 和其方差 $\sigma _{I}^{2}$。对于它不包含的每个资产 $i$，然后估计其平均收益 $r_{i}$ 及其与初始投资组合的协方差 $cov_{i}$。然后我们计算该资产的 $\beta _{i}$ **相对于初始投资组合**。

$\beta _{i}={\frac {cov_{i}}{\sigma _{I}^{2}}}$

如果 ${\frac {r_{i}-r_{f}}{r_{I}-r_{f}}}>\beta _{i}$，那么将资产 $i$ 纳入初始投资组合是有价值的。如果这样选择的新的资产被很好地分散，这种方法会比初始方法得到更好的投资组合。它可以同时具有更高的收益和更低的风险。通过迭代该过程，人们可以希望找到一个最优的投资组合并战胜市场。

CAPM 是由 Jack Treynor（1961 年，1962 年），William F. Sharpe（1964 年），John Lintner（1965 年）和 Jan Mossin（1966 年）独立提出的，其基础是 Harry Markowitz 关于多元化和现代投资组合理论的早期工作。（维基百科）

收益的预期值通常是不可测量的。

要测量随机变量$X$的期望值$\mu$，且该变量的标准差为$\sigma$，我们至少需要进行$100({\frac {\sigma }{\mu }})^{2}$次独立测量。

证明：使用$n$次独立测量得到的平均值$\mu _{n}$本身就是一个随机变量

$\mu _{n}={\frac {1}{n}}\sum _{i=1}^{n}X_{i}$，其中$X_{i}$是与$X$服从相同分布的独立随机变量。

$\mu _{n}$的期望值显然是$\mu$，其标准差为

$\sigma _{n}={\frac {\sigma }{\sqrt {n}}}$

为了使测量结果有意义，$\sigma _{n}$必须远小于$\mu _{n}$。当${\frac {\sigma _{n}}{\mu _{n}}}<{\frac {1}{10}}$时，我们可以期望得到对$\mu$的正确估计，但这仍然是一个非常不精确的测量结果，因为$\mu _{n}$偏离$\mu$超过20%的概率大约为0.04。

${\frac {\sigma _{n}}{\mu }}<{\frac {1}{10}}$要求$n>100({\frac {\sigma }{\mu }})^{2}$

股票的年收益率通常在 6% 到 30% 之间，有时会更低。12% 是一个典型值。这些收益率的标准差通常在 10% 到 60% 之间。15% 是一个典型值。所以 $\sigma /\mu \approx 1$ 甚至更高。需要超过一个世纪的年收益率测量才能获得其预期值的粗略估计。但我们没有一个世纪，只有几年，因为没有理由让收益率的预期值在几年以上保持不变。如果我们测量月度收益率，我们将测量次数增加 12 倍，但 $(\sigma /\mu )^{2}$ 也增加了 12 倍。所以结论没有改变。一般来说，收益率的预期值是不可测量的（Luenberger 1998）。

除非投资风险很低，否则测量的平均收益率并不是理论平均收益率的估计值，因为在这种情况下 $\sigma /\mu$ 在 1 前面很小。这意味着收益率变化的概率模型无法直接与现实进行比较，因为无法衡量其最重要的参数，即收益率的预期值。这并不奇怪，因为一般来说，理论概率在经济学中没有客观意义，因为经济事件不可重复。

由于收益率变化的概率模型无法直接与现实进行比较，人们可能会得出结论，这些模型没有科学价值，但这是一个夸大的结论，因为这些模型仍然可以得出可观察的预测。它们有时在解释我们的观察结果方面非常有用，即使我们无法测量所有参数。

CAPM 假设代理人知道收益率的预期值来做出投资选择。由于这些预期值通常无法测量，因此代理人无法知道它们。事实上，这些收益率的预期值纯粹是理论上的，并不存在。但不能因此得出 CAPM 完全不现实的结论。代理人会估计预期收益率并根据其估计做出决策。如果代理人得到充分的资讯，则预期收益率可能不是最终实现的收益率的太差估计值。

通过时间分散化降低风险

考虑一项非常冒险的投资，它允许投资者在短期内以 $k>2$ 的倍数增加其资本，概率为 $0.5$，或者失去所有资金。其平均效率为 $k/2-1$。但是，如果我们将所有资金投资于 $n$ 个连续时期，我们破产的概率为 $1-(1/2)^{n}$。如果 $n$ 很大，破产几乎是确定的，我们不会从平均收益中受益。是否可以利用这种平均收益率而不承担风险？

与其冒着损失所有资本的风险，我们可以选择动态管理资金，并在每个周期只押注一小部分 $\alpha$ 到这种高风险投资上。在每个周期，平均收益率仅为 $\alpha (k/2-1)$。我们有二分之一的概率将我们的资本乘以 $1-\alpha$，也有二分之一的概率将它乘以 $1+(k-1)\alpha$。设 $V_{0}=1$ 为初始资本值，而 $V_{n}$ 为其在 n 个周期后的价值。n 个周期后的对数效率 $\ln(V_{n}/V_{0})=\ln(V_{n})$ 是具有均值 $[\ln(1-\alpha )+\ln(1+(k-1)\alpha )]/2$ 和方差 $[\ln(1-\alpha )-\ln(1+(k-1)\alpha )]^{2}/4$ 的独立随机变量之和。当 n 很大时，$\ln V_{n}$ 的分布趋于均值为 $n[\ln(1-\alpha )+\ln(1+(k-1)\alpha )]/2$，方差为 $n[\ln(1-\alpha )-\ln(1+(k-1)\alpha )]^{2}/4$ 的正态分布。

对数收益率均值的标准差比率 ${\frac {|\ln(1-\alpha )-\ln(1+(k-1)\alpha )|}{{\sqrt {n}}[\ln(1-\alpha )+\ln(1+(k-1)\alpha )]}}$ 当 n 非常大时趋于零。如果每个周期的对数收益率的平均值是正数，$[\ln(1-\alpha )+\ln(1+(k-1)\alpha )]/2>0$ 那么当 n 非常大时，我们可以进行无风险盈利。如果 $\alpha <(k-2)/(k-1)$，这种动态管理策略只要周期数足够大就能带来一定的收益。

这种风险降低策略是基于时间分散的。它假设给定期间的利润与之前期间的利润无关。通过增加有风险但统计上独立的利润，降低了风险。

布莱克-斯科尔斯公式

布莱克-斯科尔斯公式可以根据标的资产的现值 $S_{t}$、波动率 $\sigma$、到期时间 $T$、期权执行价格 $K$ 以及无风险利率 $r$ 计算欧式看涨期权或看跌期权的现值。

证明它们最简单的方法是在风险中性经济体中进行推理。这意味着风险溢价始终为零。这个假设显然完全错误，但令人惊讶的是，它得出了正确的公式。下面给出的布莱克-斯科尔斯方程不需要风险中性的假设，并证明了同名公式的合理性。更一般地说，风险中性的假设通常使我们能够正确评估衍生产品，尽管这些产品非常危险，因为这些产品的价值基于其标的资产的现值。这些市场价格考虑了所需的风险溢价。如果风险溢价发生变化，例如，由于代理人对风险更加害怕，市场价格也会发生变化，但它们与衍生品价格之间的关系不会改变（Hull 2011）。这就是为什么在根据标的资产价格估值衍生品价格时，通常可以忽略风险溢价的原因。后面介绍的二叉树模型可以更清楚地证明这一点。

风险中性和资产价值

假设代理人是风险中性的。然后，资产的现值等于其预期值的现值的平均值

$S_{0}=\langle e^{-rT}S_{T}\rangle$

其中 $r$ 是无风险利率。对于价格变化由参数为 $\mu$ 和 $\sigma$的对数正态分布决定的股票，我们可以推导出

$\langle S_{T}\rangle =e^{rT}S_{0}=e^{(\mu +\sigma ^{2}/2)T}S_{0}$

因此

$r=\mu +\sigma ^{2}/2$

欧式看涨期权的现值

如果 $S_{T}$ 是标的资产的预期价值， $max(S_{T}-K,0)$ 是行权价为 $K$ 的看涨期权的预期价值 $C_{T}$ 。风险中性要求其现值 $C_{0}$ 是其预期价值的现值的平均值

$C_{0}={\frac {e^{-rT}}{\sigma {\sqrt {T}}{\sqrt {2\pi }}}}\int _{K}^{+\infty }{\frac {S-K}{S}}e^{-(\ln {\frac {S}{S_{0}}}-\mu T)^{2}/2T\sigma ^{2}}dS$

$={\frac {e^{-rT}}{\sigma {\sqrt {T}}{\sqrt {2\pi }}}}(\int _{K}^{+\infty }e^{-(\ln {\frac {S}{S_{0}}}-\mu T)^{2}/2T\sigma ^{2}}dS-\int _{K}^{+\infty }{\frac {K}{S}}e^{-(\ln {\frac {S}{S_{0}}}-\mu T)^{2}/2T\sigma ^{2}}dS)$

$=C_{+}-C_{-}$

用 $x=\ln {\frac {S}{S_{0}}}$ ， $S=S_{0}e^{x}$ ， $dS=S_{0}e^{x}dx$

$C_{+}={\frac {S_{0}e^{-rT}}{\sigma {\sqrt {T}}{\sqrt {2\pi }}}}\int _{\ln {\frac {K}{S_{0}}}}^{+\infty }e^{x-(x-\mu T)^{2}/2T\sigma ^{2}}dx$

现在 $x-(x-\mu T)^{2}/2T\sigma ^{2}=-(x-(\mu +\sigma ^{2})T)^{2}/2T\sigma ^{2}+\mu T+\sigma ^{2}/2$

因此

$C_{+}=S_{0}e^{(-r+\mu +\sigma ^{2}/2)T}{\frac {1}{\sigma {\sqrt {T}}{\sqrt {2\pi }}}}\int _{\ln {\frac {K}{S_{0}}}}^{+\infty }e^{-(x-(\mu +\sigma ^{2})T)^{2}/2T\sigma ^{2}}dx=S_{0}{\frac {1}{\sigma {\sqrt {T}}{\sqrt {2\pi }}}}\int _{\ln {\frac {K}{S_{0}}}}^{+\infty }e^{-(x-(\mu +\sigma ^{2})T)^{2}/2T\sigma ^{2}}dx$

由于 $r=\mu +\sigma ^{2}/2$

以 $y=(x-(\mu +\sigma ^{2})T)/\sigma {\sqrt {T}}$，$dx=\sigma {\sqrt {T}}dy$

$C_{+}=S_{0}{\frac {1}{\sqrt {2\pi }}}\int _{(\ln {\frac {K}{S_{0}}}-(\mu +\sigma ^{2})T)/\sigma {\sqrt {T}}}^{+\infty }e^{-y^{2}/2}dy$

设 $N(.)$ 为标准正态分布的累积分布函数

$N(x)={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{x}e^{-y^{2}/2}dy$

由于 ${\frac {1}{\sqrt {2\pi }}}\int _{x}^{+\infty }e^{-y^{2}/2}dy={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{-x}e^{-y^{2}/2}dy=N(-x)$

$C_{+}=S_{0}N[(\ln {\frac {S_{0}}{K}}+(\mu +\sigma ^{2})T)/\sigma {\sqrt {T}}]=S_{0}N[(\ln {\frac {S_{0}}{K}}+(r+\sigma ^{2}/2)T)/\sigma {\sqrt {T}}]$

$C_{-}={\frac {e^{-rT}}{\sigma {\sqrt {T}}{\sqrt {2\pi }}}}\int _{K}^{+\infty }{\frac {K}{S}}e^{-(\ln {\frac {S}{S_{0}}}-\mu T)^{2}/2T\sigma ^{2}}dS={\frac {Ke^{-rT}}{\sigma {\sqrt {T}}{\sqrt {2\pi }}}}\int _{\ln {\frac {K}{S_{0}}}}^{+\infty }e^{-(x-\mu T)^{2}/2T\sigma ^{2}}dx$

用 $z=(x-\mu T)/\sigma {\sqrt {T}}$，$dx=\sigma {\sqrt {T}}dz$

$C_{-}=Ke^{-rT}{\frac {1}{\sqrt {2\pi }}}\int _{(\ln {\frac {K}{S_{0}}}-\mu T)/\sigma {\sqrt {T}}}^{+\infty }e^{-z^{2}/2}dz$

$=Ke^{-rT}N[(\ln {\frac {S_{0}}{K}}+\mu T)/\sigma {\sqrt {T}}]=Ke^{-rT}N[(\ln {\frac {S_{0}}{K}}+(r-\sigma ^{2}/2)T)/\sigma {\sqrt {T}}]$

最后

$C_{0}=S_{0}N[(\ln {\frac {S_{0}}{K}}+(r+\sigma ^{2}/2)T)/\sigma {\sqrt {T}}]-Ke^{-rT}N[(\ln {\frac {S_{0}}{K}}+(r-\sigma ^{2}/2)T)/\sigma {\sqrt {T}}]$

这是欧式看涨期权的布莱克-斯科尔斯公式。

欧式看跌期权的现值

如果 $S_{T}$ 是标的资产的预期价值，$max(K-S_{T},0)$ 是行权价为 $K$ 的看跌期权的预期价值 $P_{T}$。风险中性要求其现值 $P_{0}$ 是其预期值的现值的平均值

$P_{0}={\frac {e^{-rT}}{\sigma {\sqrt {T}}{\sqrt {2\pi }}}}\int _{0}^{K}{\frac {K-S}{S}}e^{-(\ln {\frac {S}{S_{0}}}-\mu T)^{2}/2T\sigma ^{2}}dS=P_{+}-P_{-}$

$P_{+}={\frac {e^{-rT}}{\sigma {\sqrt {T}}{\sqrt {2\pi }}}}\int _{0}^{K}{\frac {K}{S}}e^{-(\ln {\frac {S}{S_{0}}}-\mu T)^{2}/2T\sigma ^{2}}dS={\frac {Ke^{-rT}}{\sigma {\sqrt {T}}{\sqrt {2\pi }}}}\int _{-\infty }^{\ln {\frac {K}{S_{0}}}}e^{-(x-\mu T)^{2}/2T\sigma ^{2}}dx$

$=Ke^{-rT}{\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{(\ln {\frac {K}{S_{0}}}-\mu T)/\sigma {\sqrt {T}}}e^{-z^{2}/2}dz$

$=Ke^{-rT}N[(\ln {\frac {K}{S_{0}}}-\mu T)/\sigma {\sqrt {T}}]=Ke^{-rT}N[(\ln {\frac {K}{S_{0}}}-(r-\sigma ^{2}/2)T)/\sigma {\sqrt {T}}]$

$P_{-}={\frac {e^{-rT}}{\sigma {\sqrt {T}}{\sqrt {2\pi }}}}\int _{0}^{K}e^{-(\ln {\frac {S}{S_{0}}}-\mu T)^{2}/2T\sigma ^{2}}dS=S_{0}e^{(-r+\mu +\sigma ^{2}/2)T}{\frac {1}{\sigma {\sqrt {T}}{\sqrt {2\pi }}}}\int _{-\infty }^{\ln {\frac {K}{S_{0}}}}e^{-(x-(\mu +\sigma ^{2})T)^{2}/2T\sigma ^{2}}dx$

$=S_{0}{\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{(\ln {\frac {K}{S_{0}}}-(\mu +\sigma ^{2})T)/\sigma {\sqrt {T}}}e^{-y^{2}/2}dy$

$=S_{0}N[(\ln {\frac {K}{S_{0}}}-(\mu +\sigma ^{2})T)/\sigma {\sqrt {T}}]=S_{0}N[(\ln {\frac {K}{S_{0}}}-(r+\sigma ^{2}/2)T)/\sigma {\sqrt {T}}]$

最后

$P_{0}=Ke^{-rT}N[(\ln {\frac {K}{S_{0}}}-(r-\sigma ^{2}/2)T)/\sigma {\sqrt {T}}]-S_{0}N[(\ln {\frac {K}{S_{0}}}-(r+\sigma ^{2}/2)T)/\sigma {\sqrt {T}}]$

这是欧式看跌期权的 Black-Scholes 公式。

Black-Scholes 方程

原则上，风险对冲策略可用于构建包含期权和股票或其他资产的无风险投资组合。该技术简单地是对冲涨跌。投资组合中一个或多个项目的收益率高于无风险利率的任何涨幅，都会被其他项目的跌幅或低于无风险利率的涨幅抵消。因此，此类投资组合的回报率为无风险利率。涨跌会机械地抵消。但在支付风险溢价的经济体中，无风险投资组合与不支付风险溢价的经济体中的无风险投资组合相同，而 Black-Scholes 公式则决定了它们的组成。不同的公式必然会导致组成不同的无风险投资组合。由于无风险投资组合无论经济体是否风险中性都相同，因此 Black-Scholes 公式的有效性并不依赖于风险溢价的存在。

更确切地说，我们将从无风险投资组合的存在证明，确定期权价值的函数必须满足一个偏微分方程，即 Black-Scholes 方程。同名公式是此方程中满足边界条件的唯一解。

令 $V(t,S)$ 为基于标的资产当前价格 $S$，在时间 $t$ 的期权价值。如果 $V(t,S)$ 是市场价格，则可以通过经验获得。从先验角度来看，它可能取决于风险溢价，因为买卖期权是风险交易。Black-Scholes 关于无风险投资组合的推理表明，$V(t,S)$ 实际上与风险溢价无关。

无风险投资组合是在时间 $t$ 持有一个期权和 $-{\frac {\partial V}{\partial S}}$ 个标的资产单位构建的。如果 ${\frac {\partial V}{\partial S}}>0$，则需要卖空标的资产。

如前所述，我们假设标的资产的随机波动由对数正态分布描述。

在时间间隔 $dt$ 内，$S$ 的变化 $dS$ 是两项之和

${\frac {dS}{S}}=mdt+\sigma \epsilon {\sqrt {dt}}$

其中 $\epsilon$ 是一个标准正态随机变量。

要计算 $dV$，公式 $dV=({\frac {\partial V}{\partial t}}+{\frac {\partial V}{\partial S}}{\frac {dS}{dt}})dt$ 不适用，因为当 $t$ 趋于零时，${\frac {dS}{dt}}$ 发散。

以下关于数量级的推理并不严格，但它会导致一个精确的公式，该公式可以用伊藤引理证明。

$dV={\frac {\partial V}{\partial t}}dt+{\frac {\partial V}{\partial S}}dS+{\frac {1}{2}}{\frac {\partial ^{2}V}{\partial S^{2}}}dS^{2}$

${\frac {dS^{2}}{S^{2}}}=m^{2}dt^{2}+m\sigma \epsilon dt^{3/2}+\sigma ^{2}\epsilon ^{2}dt$

当 $dt$ 趋于零时，前两项与第三项相比可以忽略不计。

假设我们可以用 $1$ 的平均值替换 $\epsilon ^{2}$，我们得到

$dV=({\frac {\partial V}{\partial t}}+mS{\frac {\partial V}{\partial S}}+S^{2}{\frac {\sigma ^{2}}{2}}{\frac {\partial ^{2}V}{\partial S^{2}}})dt+S{\frac {\partial V}{\partial S}}dW$

无风险投资组合的价值变化是

$d\Pi =dV-{\frac {\partial V}{\partial S}}dS=({\frac {\partial V}{\partial t}}+S^{2}{\frac {\sigma ^{2}}{2}}{\frac {\partial ^{2}V}{\partial S^{2}}})dt$

随机项 $dW$ 消失了。这证实了该投资组合是无风险的。

$\Pi$ 必须以无风险利率 $r$ 变化

$d\Pi =r\Pi dt=r(V-{\frac {\partial V}{\partial S}}S)dt$

我们得到

${\frac {\partial V}{\partial t}}+S^{2}{\frac {\sigma ^{2}}{2}}{\frac {\partial ^{2}V}{\partial S^{2}}}=r(V-{\frac {\partial V}{\partial S}}S)$

这是布莱克-斯科尔斯方程。

${\frac {\partial V}{\partial t}}+S^{2}{\frac {\sigma ^{2}}{2}}{\frac {\partial ^{2}V}{\partial S^{2}}}+rS{\frac {\partial V}{\partial S}}-rV=0$

可以验证布莱克-斯科尔斯的公式是同名方程的解。该方程不需要风险中性环境的假设。因此，布莱克-斯科尔斯的公式在非风险中性环境中也是成立的。二叉树模型为这一结果提供了更简单的解释。

二叉树和风险中性

以下例子非常简单，也非常不现实，但足以理解为什么期权和股票价格之间的关系不依赖于风险溢价。

假设今天价值为 100 的股票，在下一期可能以 p 的概率变为 110，或者以 1-p 的概率变为 90。现在想知道执行价格为 110 的看跌期权的当前价格 P。为了简便起见，假设无风险利率为零。包含一只股票和一只期权的投资组合的当前价格为 100 + P。它的未来价值在任何情况下都是 110。因此，它是无风险的。我们推导出 P = 10。我们不需要知道涨价的概率来知道期权的价格。我们不需要知道投资者承担的风险及其风险溢价。

更一般地，单期二叉树模型由以下参数定义：p、u、d 和 r。p 是股票价格在下一期乘以 u（上涨）的概率，1-p 是股票价格乘以 d（下跌）的概率。r 是单期的无风险利率。

假设股票的当前价格为 100，u> 1 且 d <1。为了评估执行价格为 K 的看跌期权的当前价格 P，我们考虑一个包含 $\Delta$ 股股票和一只期权的投资组合。假设 $100d\leq K\leq 100u$。投资组合的当前价格为 $100\Delta +P$。它的未来价值要么是 $100u\Delta$，要么是 $100d\Delta +K-100d$。当

$100u\Delta =100d\Delta +K-100d$

也就是说

$\Delta ={\frac {K-100d}{100(u-d)}}$

由于它是安全的，我们必须有

$(100\Delta +P)(1+r)=100u\Delta$

所以

$P=\frac{100\mathrm{\Delta }(u-1-r)}{1+r}=\frac{(K-100d)(u-1-r)}{(u-d)(1+}$

为了找出行使价格为 K 的看涨期权的现价 C，我们可以考虑一个组合，该组合由卖出 $\Delta$ 股股票做空，并买入一份期权组成。卖空是指卖出借来的股票，并承诺以后买回它们来归还。该组合的现价为 $-100\Delta +C$。它的未来价值要么是 $-100u\Delta +100u-K$，要么是 $-100d\Delta$。当满足以下条件时，该组合是无风险的

$-100u\Delta +100u-K=-100d\Delta$

也就是说

$\Delta ={\frac {K-100u}{100(d-u)}}$

由于它是安全的，我们必须有

$(-100\Delta +C)(1+r)=-100d\Delta$

所以

$C={\frac {100\Delta (1+r-d)}{1+r}}={\frac {(K-100u)(1+r-d)}{(d-u)(1+r)}}$

与第一个例子一样，我们不需要知道涨幅的概率 p 就能知道期权的价格。因此，我们不需要知道风险溢价来评估看跌期权和看涨期权。

当然，假设股票在一段时间后只有两个值是不现实的。但只要期数足够多，对多期二叉树进行推理就足以使模型非常现实。用两个时期，可以得到三个可能的未来值：100uu、100ud 和 100dd。用 N 个时期，可以得到 N + 1 个可能的未来值。如果 N 非常大，股票价格的变化遵循对数正态分布。我们可以通过对二叉树进行推理来证明布莱克-斯科尔斯公式。因此，用二叉树建立的期权价格与风险溢价无关性，比模型简单性在开始时所暗示的要现实得多。

科克斯、罗斯和鲁宾斯坦的论文《期权定价：一种简化方法》（1979 年）是开创性的论文，它展示了该模型的价值。

看跌期权的平均收益率可能为负。

如果标的股票的 $\beta$ 为正，那么看跌期权的 $\beta$ 为负。我们将在一个例子中展示，$\beta$ 可以足够负以使平均收益率为负。

考虑一只股票，其平均收益率（算术年化）为 10%，波动率为 20%。

$\mu =0.08$

$\sigma =0.2$

$e^{\mu +\sigma ^{2}/2}-1\approx 0.1$

我们对一个 6 个月的看跌期权进行推理，其执行价格等于股票的当前价格加上其平均收益率。

设 $V_{0}=100$ 为股票的现价。期权的执行价格为

$K=V_{0}e^{(\mu +\sigma ^{2}/2)T}=100e^{(0.08+0.2^{2}/2)0.5}\approx 105.13$

使用 Black 和 Scholes 公式可以得到期权的现价

$P_{0}=Ke^{-rT}N[(\ln {\frac {K}{S_{0}}}-(r-\sigma ^{2}/2)T)/\sigma {\sqrt {T}}]-S_{0}N[(\ln {\frac {K}{S_{0}}}-(r+\sigma ^{2}/2)T)/\sigma {\sqrt {T}}]$

其中 $r=0.02$, $P_{0}\approx 8.02$,

期权在行权日平均将产生 $\langle P_{f}\rangle$

$\langle P_{f}\rangle =KN[(\ln {\frac {K}{S_{0}}}-\mu T)/\sigma {\sqrt {T}}]-S_{0}e^{rT}N[(\ln {\frac {K}{S_{0}}}-(\mu +\sigma ^{2})T)/\sigma {\sqrt {T}}]$

$\approx 7.87$

因此期权的平均年对数收益率为

$2\ln {\frac {7.87}{8.02}}\approx -0.038=-3.8\%$

数学补充

正态分布

概率密度

• 当随机变量 $X$ 的概率密度为时，它遵循 **标准正态分布**

$f_{X}(x)={\frac {1}{\sqrt {2\pi }}}e^{-x^{2}/2}$

${\frac {1}{\sqrt {2\pi }}}$ 是一个归一化因子，使概率之和等于 1

$\int _{-\infty }^{+\infty }f_{X}(x)dx={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{+\infty }e^{-x^{2}/2}dx=1$

可以通过以下推理来证明

$\int _{-\infty }^{+\infty }\int _{-\infty }^{+\infty }e^{-(x^{2}+y^{2})}dxdy=\int _{-\infty }^{+\infty }e^{-x^{2}}dx\int _{-\infty }^{+\infty }e^{-y^{2}}dy=(\int _{-\infty }^{+\infty }e^{-x^{2}}dx)^{2}$

$=\int _{0}^{2\pi }\int _{0}^{+\infty }e^{-r^{2}}rd\phi dr=2\pi [-{\frac {1}{2}}e^{-r^{2}}]_{0}^{+\infty }=\pi$

因此 $\int _{-\infty }^{+\infty }e^{-x^{2}}dx={\sqrt {\pi }}$

当 $x=y/{\sqrt {2}}$, $dx=dy/{\sqrt {2}}$，我们得到 $\int _{-\infty }^{+\infty }e^{-x^{2}}dx={\frac {1}{\sqrt {2}}}\int _{-\infty }^{+\infty }e^{-y^{2}/2}dy$

因此

$\int _{-\infty }^{+\infty }e^{-y^{2}/2}dy={\sqrt {2\pi }}$

• 一个随机变量 $X$ 服从 **中心正态分布**，当其概率密度函数为

$f_{X}(x)={\frac {1}{\sigma {\sqrt {2\pi }}}}e^{-x^{2}/2\sigma ^{2}}$

当 $y=x/\sigma$，$dx=\sigma dy$，我们可以验证 $\int _{-\infty }^{+\infty }f_{X}(x)dx={\frac {\sigma }{\sigma {\sqrt {2\pi }}}}\int _{-\infty }^{+\infty }e^{-y^{2}/2}dy=1$

• 一个随机变量 $X$ 服从正态分布，当它的概率密度函数为

$f_{X}(x)={\frac {1}{\sigma {\sqrt {2\pi }}}}e^{-(x-\mu )^{2}/2\sigma ^{2}}$

当 $y=x-\mu$，$dy=dx$，我们可以验证 $\int _{-\infty }^{+\infty }f_{X}(x)dx={\frac {1}{\sigma {\sqrt {2\pi }}}}\int _{-\infty }^{+\infty }e^{-y^{2}/2\sigma ^{2}}dy=1$

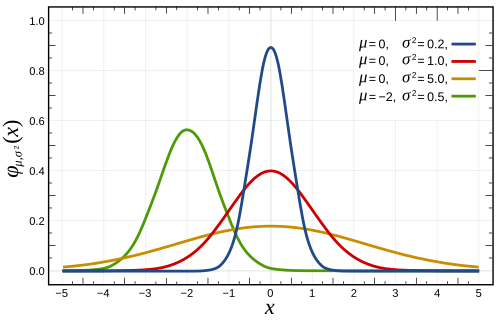
红色曲线是标准正态分布。

期望值

一个随机变量 $X$ 当它的均值，或者说期望值 $E(X)$ 为零时，称其为中心化的。由于中心化正态分布的概率密度函数是偶函数，所以很容易验证它的均值为零。$E(X)=\int _{-\infty }^{+\infty }xf_{X}(x)dx$ 是一个奇函数的积分，因此结果为零。

当 $y=x-\mu$，我们得到正态分布的期望值为

$E(X)={\frac {1}{\sigma {\sqrt {2\pi }}}}\int _{-\infty }^{+\infty }xe^{-(x-\mu )^{2}/2\sigma ^{2}}dx={\frac {1}{\sigma {\sqrt {2\pi }}}}\int _{-\infty }^{+\infty }(y+\mu )e^{-y^{2}/2\sigma ^{2}}dy=\mu$

方差和标准差

• 我们通过分部积分获得标准正态随机变量$X$的方差

$Var(X)={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{+\infty }x^{2}e^{-x^{2}/2}dx={\frac {1}{\sqrt {2\pi }}}([-xe^{-x^{2}/2}]_{-\infty }^{+\infty }-\int _{-\infty }^{+\infty }-e^{-x^{2}/2}dx)=1$

• 用$y=x/\sigma$，$dx=\sigma dy$，然后我们得到中心正态律的方差

$Var(X)={\frac {1}{\sigma {\sqrt {2\pi }}}}\int _{-\infty }^{+\infty }x^{2}e^{-x^{2}/2\sigma ^{2}}dx={\frac {1}{\sigma {\sqrt {2\pi }}}}\int _{-\infty }^{+\infty }\sigma ^{2}y^{2}e^{-y^{2}/2}\sigma dy=\sigma ^{2}$

• 正态分布的方差是相同的

$Var(X)={\frac {1}{\sigma {\sqrt {2\pi }}}}\int _{-\infty }^{+\infty }(x-\mu )^{2}e^{-(x-\mu )^{2}/2\sigma ^{2}}dx={\frac {1}{\sigma {\sqrt {2\pi }}}}\int _{-\infty }^{+\infty }y^{2}e^{-y^{2}/2\sigma ^{2}}dy=\sigma ^{2}$

$\sigma$ 因此是标准差 ${\sqrt {Var(X)}}$ 的 $X$.

对于正态分布，$\sigma$ 也是对均值绝对偏差的平均值的一个很好的估计

${\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{+\infty }|x|e^{-x^{2}/2}dx=2{\frac {1}{\sqrt {2\pi }}}\int _{0}^{+\infty }xe^{-x^{2}/2}dx$

$={\sqrt {\frac {2}{\pi }}}[-e^{-x^{2}/2}]_{0}^{+\infty }={\sqrt {\frac {2}{\pi }}}$

因此

${\frac {1}{\sigma {\sqrt {2\pi }}}}\int _{-\infty }^{+\infty }|x-\mu |e^{-(x-\mu )^{2}/2\sigma ^{2}}dx=\sigma {\sqrt {\frac {2}{\pi }}}\approx 0.8\sigma$

对数正态分布

概率密度

令 $X$ 是一个随机变量，使得 $\ln X$ 遵循均值为 $\mu$ 且标准差为 $\sigma$ 的正态分布。

$X$ 的累积分布函数是

$F_{X}(x)=Pr(X\leq x)=Pr(\ln X\leq \ln x)=F_{\ln X}(\ln x)$

因此，$X$ 的概率密度为

$f_{X}(x)={\frac {d}{dx}}F_{X}(x)={\frac {1}{x}}f_{\ln X}(\ln x)={\frac {1}{x\sigma {\sqrt {2\pi }}}}e^{-{\frac {(\ln x-\mu )^{2}}{2\sigma ^{2}}}}$

一些对数正态密度函数具有相同的参数 $\mu$，但参数 $\sigma$ 不同。

期望值

$\langle X\rangle ={\frac {1}{\sigma {\sqrt {2\pi }}}}\int _{0}^{+\infty }xf_{X}(x)dx={\frac {1}{\sigma {\sqrt {2\pi }}}}\int _{0}^{+\infty }e^{-(\ln x-\mu )^{2}/2\sigma ^{2}}dx$

用 $y=\ln x$，$x=e^{y}$，$dy={\frac {dx}{x}}$，$dx=e^{y}dy$

$\langle X\rangle ={\frac {1}{\sigma {\sqrt {2\pi }}}}\int _{-\infty }^{+\infty }e^{y-(y-\mu )^{2}/2\sigma ^{2}}dy$

现在 $y-(y-\mu )^{2}/2\sigma ^{2}=-(y-(\mu +\sigma ^{2}))^{2}/2\sigma ^{2}+\mu +\sigma ^{2}/2$

因此

$\langle X\rangle =e^{\mu +\sigma ^{2}/2}{\frac {1}{\sigma {\sqrt {2\pi }}}}\int _{-\infty }^{+\infty }e^{-(y-(\mu +\sigma ^{2}))^{2}/2\sigma ^{2}}dx$

$=e^{\mu +\sigma ^{2}/2}$

方差和标准差

$\langle X^{2}\rangle ={\frac {1}{\sigma {\sqrt {2\pi }}}}\int _{0}^{+\infty }x^{2}f_{X}(x)dx={\frac {1}{\sigma {\sqrt {2\pi }}}}\int _{0}^{+\infty }xe^{-(\ln x-\mu )^{2}/2\sigma ^{2}}dx$

令 $y=\ln x$, 则 $x=e^{y}$, $dx=e^{y}dy$

$\langle X^{2}\rangle ={\frac {1}{\sigma {\sqrt {2\pi }}}}\int _{-\infty }^{+\infty }e^{2y-(y-\mu )^{2}/2\sigma ^{2}}dy$

现在 $2y-(y-\mu )^{2}/2\sigma ^{2}=-(y-(\mu +2\sigma ^{2}))^{2}/2\sigma ^{2}+2(\mu +\sigma ^{2})$

因此

$\langle X^{2}\rangle =e^{-2(\mu +\sigma ^{2})}{\frac {1}{\sigma {\sqrt {2\pi }}}}\int _{-\infty }^{+\infty }e^{-(y-(\mu +2\sigma ^{2}))^{2}/2\sigma ^{2}}dx$

$=e^{2(\mu +\sigma ^{2})}$

$Var(X)=\langle X^{2}\rangle -\langle X\rangle ^{2}=e^{2(\mu +\sigma ^{2})}-(e^{\mu +\sigma ^{2}/2})^{2}$

$=(e^{2\mu +\sigma ^{2}})(e^{\sigma ^{2}}-1)$

因此，$X$ 的标准差为

${\sqrt {Var(X)}}=e^{\mu +\sigma ^{2}/2}{\sqrt {e^{\sigma ^{2}}-1}}$