三维电子显微镜/3D 重建
外观
< 三维电子显微镜

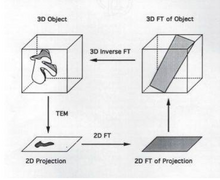



在透射电子显微镜中,3D 重建的目标是将 2D 投影转换为其 3D 体积。这使得可以可视化样本中的微小结构。重建 2D 投影至关重要,因为从投影本身获得的信息有限。
投影发生在将 3D 图像拍摄并将其点放置在 2D 平面上时。2D 平面中的每个点对应于 3D 体积中的一个切片,并且基于拉东定理。可以获得 3D 体积,获取 2D 投影,随后对投影进行傅里叶变换,并使用投影的傅里叶变换来获得 3D 体积的“切片”。此后,可以对“切片”进行逆傅里叶变换,得到 3D 体积。
在进行重建之前,有必要知道粒子朝哪个方向。可以使用粒子的欧拉角来确定粒子的方向。欧拉角可以通过两种方式定义。根据第一个定义,可以使用纬度、经度和粒子位置的旋转来确定方向。第二个定义考虑了 z 轴和 x 轴。使用 Z 轴确定初始位置。接下来,旋转粒子,并从新的 X 轴推导出方向。第三个也是最后一个计算基于新的 Z 轴的位置,它已经绕其 x 轴旋转。
反投影基本上是拉东变换的逆变换。它是一个将 2D 投影转换为 3D 模型的过程。它是唯一可用于此目的的方法。反投影通过获取每个视图并将其沿着获取它的相同路径进行涂抹来重建图像(图 1)。由此产生的结果是正确图像的模糊版本(Voss 2013)[1]。
获得 3D 重建后,重要的是确定重建质量。这可以通过使用傅里叶壳相关性来完成。基本上,粒子集被分成一个偶数子集和一个奇数子集,其中为每个子集计算一个结构。然后将每个子集反投影以获得每个子集的体积。由于目标是确定重建的质量,因此数据被分成傅里叶空间中的环,每个环代表不同的分辨率。然后,根据其频率计算偶数子集结构与奇数子集结构之间的相关系数。

- ↑ Voss, Neil. 3D 重建。蛋白质结构 464。罗斯福大学,沙弗堡,伊利诺伊州。2013 年 10 月 25 日。讲座。
