 这里
这里 
余弦定理解释了三角形边长和一个角之间的关系。该定理指出,对于任意三角形  ,如果
,如果  ,
, ,
, 和
和  ,则
,则  。对于
。对于  是一个直角三角形,并且
是一个直角三角形,并且  ,我们之前已经将其证明为勾股定理。
,我们之前已经将其证明为勾股定理。
在任何三角形中,一条边长的平方等于其他两条边长的平方和减去这两条边长乘积的两倍以及它们所夹角的余弦值的差。
假设, 是一个三角形,其中
是一个三角形,其中 

 和
和  需要证明的是,
需要证明的是, 。
。
让我们将线段  延长至
延长至  (仅适用于钝角三角形),其中
(仅适用于钝角三角形),其中  。假设
。假设  以及
以及  .
.
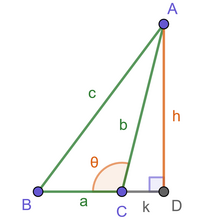 证明角为
证明角为  的余弦定律的构造。
的余弦定律的构造。
根据勾股定理,我们可以说,对于 

类似地,对于三角形 


 .
.
我们将使用这个值进行进一步的证明。但现在,让我们确定三角形的一些三角函数值。
这里, .
.
因此,
或者,
![{\displaystyle =b[\cos(\pi )\cdot cos(\theta )+\sin(\pi )\cdot \sin(\theta )]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1da982b5b73a75c5f627c5c65f72c819bcdee6e4)

现在, .
.
 . [证明完毕]
. [证明完毕]
 证明余弦定理对于角度
证明余弦定理对于角度 的构造。
的构造。
就像我们之前证明的那样,根据勾股定理,我们可以说,对于

类似地,对于三角形


 .
.
这里, .
.
所以,

现在, .
.
 . [证明完毕]
. [证明完毕]
[注意:无论三角形是什么,公式  都适用。]
都适用。]






























![{\displaystyle =b[\cos(\pi )\cdot cos(\theta )+\sin(\pi )\cdot \sin(\theta )]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1da982b5b73a75c5f627c5c65f72c819bcdee6e4)










