运输部署案例集/美国邮政

简介

美国邮政局 (USPS) 为美国 1.51 亿个投递点提供服务。 这一网络包括邮箱、邮局、分拣设施和送货卡车，为任何个人或企业提供将货物或信息从一个目的地运送到另一个目的地的途径。随着电子信息传输方式的可用性不断提高，成本不断降低，可以合理地预期，这一物理邮政网络的意义会随着时间的推移而下降。本文考察了美国邮局数量和邮局处理的邮件量历史数据，以确定邮政服务运输模式的诞生、增长、成熟和衰退周期。

邮政服务作为一种运输方式

中央邮政服务是一个协调的运输系统，在物理上将货物和信息在目的地之间移动。它本质上是一个货物运输系统，任何个人或企业都可以使用。

垄断和服务义务

子模式：邮局与送货上门

邮政服务的部署模式最初是邮局网络和它们之间的转运。邮局客户负责将邮件带到邮局，并从当地邮局的普通邮件中取回他们的信件和包裹。

19 世纪 60 年代，邮政服务开始在城市化地区部署上门/商业送货服务。这使得邮局能够关闭，因为对邮局客户援助的需求减少了。每个邮局能够服务更广阔的区域和更大的居民群体，因为部署了邮递员网络将邮件分发到人们的家庭和办公室。

19 世纪 90 年代，邮局开始试验农村送货上门服务，以了解其可行性。到 1901 年，农村送货上门成为邮政服务的官方政策。此时，美国邮局数量开始减少，因为越来越多的地区连接到这一送货上门网络。

这种从仅以邮局为中心的网络到扩展到连接所有居民的点对点网络的转变本质上是邮政系统内的模式转变。它改变了邮局在系统中所起的主要作用，将它们的作用从公众形象和分发点转变为协调邮递员的物流中心，邮局的平均人数随着人口增长和邮局合并而不断增加。

使能模式

邮政服务随着时间的推移而发展，以融入技术进步。最初的马车运输发展成为马车、河船、铁路、公路，最终发展成为航空货运。

竞争模式

信息技术领域的科技进步正在取代邮政服务的大部分信息传输功能。每年处理的邮件数量从 2006 年开始下降。当平均到整个人口时，每人处理的邮件数量从 2000 年开始下降。

数据

独立变量和控制变量

$T=$时间（年），1790 年至 2010 年 $P=$人口，1790 年至 2010 年

因变量

$PO=$邮局数量，1790 年至 2010 年

$M=$处理的邮件数量，1847 年至 2010 年

构建的因变量

• 废弃邮局数量 $(PO_{A})$

对于 $T>1901$， $PO_{A}=PO_{max}-PO$

• 每10000人拥有的邮局数量 $(PO_{p10k})$

$10000*PO/P$

• 每家邮局对应的人口数量 $(D)$

$D=P/PO$

• 每人处理的邮件数量 $(H)$

$H=M/P$

线性变换

因变量 $(DV)$ 经过变换以便使用线性回归模型。

$Y_{DV}=\ln {\left\lbrack Measure/(MaxDV-DV)\right\rbrack }$

方法

模型1：因变量作为时间函数，分两个阶段

• 模型1a：诞生、增长和成熟阶段，所有早于 $Y_{Max}$ 的年份
• 模型1b：成熟和衰退阶段，所有晚于 $Y_{Max}$ 的年份

$Y_{DV}={\begin{cases}f(T),&{\text{while }}T<Y_{max}\\f(T),&{\text{while }}T>Y_{max}\\\end{cases}}$

使用此模型测试的因变量

• 处理的邮件数量，$Y_{M}$
• 邮局数量，$Y_{PO}$
• 废弃的邮局数量，$Y_{PO_{A}}$，[仅限衰退阶段]
• 每10,000人拥有的邮局数量，$Y_{PO_{p10k}}$
• 每家邮局的人数，$D$
• 每人处理的邮件数量，$H$

模型 2：控制人口的随时间变化的因变量

• 模型 2a：出生、增长和成熟阶段，所有早于$Y_{Max}$的年份
• 模型 2b：成熟和衰退阶段，所有晚于$Y_{Max}$的年份

$Y_{DV}={\begin{cases}f(T,P),&{\text{while }}T<Y_{max}\\f(T,P),&{\text{while }}T>Y_{max}\\\end{cases}}$

使用此模型测试的因变量

• 处理的邮件数量，$Y_{M}$
• 邮局数量，$Y_{PO}$
• 废弃的邮局数量，$Y_{PO_{A}}$，[仅限衰退阶段]

结果

描述性统计

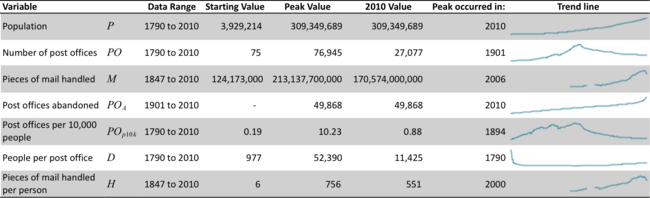
正如描述性统计表中所显示的，邮局数量和处理的邮件数量都已达到峰值。邮局数量在 1901 年达到峰值，当时 USPS 将农村家庭送货作为标准做法。邮件数量在 2006 年达到峰值。每 10,000 人拥有的邮局数量在 1800 年代非常不稳定，因为 USPS 逐步推出了家庭送货服务。

值得注意的是，每人处理的邮件数量和每 10,000 人拥有的邮局数量在处理的邮件数量和邮局数量的绝对值达到峰值之前就已达到峰值。即使在 1901 年农村家庭送货政策颁布之前，该政策导致许多邮局关闭，但所需邮局数量更少，可以为相同的人口提供服务。这可以用城市家庭送货、运营效率提高或支持性交通基础设施得到改善来解释。每人处理的邮件数量在 2000 年达到峰值，此后一直在下降。这可以用信息技术的转变以及电子传输的兴起来合理地解释，电子传输取代了实体印刷材料的交付。

相关性

因变量相关性表中显示的所有变量都与年份、人口和转换后的 人口具有统计学意义上的相关性。这些相关性的方向并不出乎意料：邮件数量随时间和人口增长而急剧增加，而邮局数量则下降。每个邮局服务的平均人数与人口呈正相关，这是由于邮局数量下降和人口不断增长造成的。

回归模型

随时间变化的处理的邮件数量

随着时间的推移，邮件量模型表明，在部署这种特定运输“方式”方面，一个不断增长的市场具有重要意义。虽然邮件量在模型 1 和 1a 中具有强烈的统计学意义系数，但在模型 2a 中控制人口因素消除了时间的影响。模型 2a 很好地拟合了这些数据的增长阶段，$R^{2}$值为 0.977。考虑到数据的参数和美国邮政署以及竞争模式的定性历史，模型 1 和模型 1a 的$T_{0}$值是合理的。

由于邮件处理量峰值出现在 2006 年，在控制人口因素的情况下，没有足够的数据点来对衰退阶段进行有意义的分析。尽管模型 1b 的 t 统计量值的大小大于 2，但该模型应谨慎考虑，因为它只包含 4 年的数据。相反，由于衰退阶段仅在最后 4 年的数据中明显，因此总体模型（模型 1 和模型 2）对数据的拟合程度几乎与增长特定模型（模型 1a 和模型 2a）一样好。

模型 1b 的$T_{0}$值强化了衰退模型的弱点：2010 年是可用数据的最后一年，因此，不能确定地期望 2010 年确实是衰退曲线的拐点。衰退模型假设，随着其他模式迅速取代邮政服务，邮件量最终将降至零，而很容易想象，随着其他模式缓慢取代邮政服务，邮政服务将保持适度的重要性。

随着时间的推移，邮局数量

与邮件量模型不同的是，邮局数量在 1901 年达到峰值，总体模型对数据的拟合程度并不高，$R^{2}$值低于 0.355。系数与我们对邮局趋势的了解不一致：模型 1 和模型 2 对时间具有正系数，而从描述性统计中的图表可以明显看出，邮局数量已经下降了一个多世纪。

增长模型和衰退模型都比总体模型更能拟合数据。模型 1a 和 1b 中的系数与预期的影响方向一致，并且具有较强的 t 统计量。在模型 2a 和 2b 中控制人口因素，可以增强时间系数，并且它们仍然具有统计学意义。控制人口因素还略微改善了增长阶段和衰退阶段的模型拟合。

虽然衰退模型在邮件量方面失败了，但邮局的衰退模型使用的数据轨迹更长，并且与邮局覆盖范围随时间推移缓慢消失的情况一致，而不是邮件量模型预测的急剧下降。

考虑到数据的参数，模型 1a 和 1b 的$T_{0}$值是合理的。

随着时间的推移，被废弃或关闭的邮局数量

这些数据只需要模型 1b 和 2b，因为邮局关闭直到 1901 年邮局数量达到峰值之后才开始。

该模型对邮局数据的拟合程度远高于 1901 年至 2010 年的简单邮局数量。模型 1b 的$R^{2}$值对于邮局关闭数据为 0.941，对于邮局数量数据为 0.747。模型 2b 的$R^{2}$值对于邮局关闭数据为 0.965，再次与邮局数量的 0.790 相比。

正如左侧曲线类型图像所示，当进行变换并调整到相同的比例时，关闭/废弃曲线更接近我们用来预测诞生、增长和成熟周期的 S 曲线函数。表示实际剩余邮局数量的曲线是该图的反转，在关闭/废弃曲线处于更平缓的诞生和成熟阶段时，会发生急剧变化。下一张图像将这些数据与使用回归系数和计算的$T_{0}$从模型 1b 中获得的预测值一起绘制。

邮件量和设施与人口模型的比率

最后三个测试的因变量都是邮件量或邮局设施与总人口的比率，因此控制人口的模型 2、2a 和 2b 已经被排除在外。

每 10,000 人的邮局数量

每家邮局的人数

每人邮件量

讨论

这些实验表明，虽然 S 型曲线模型可以很好地预测交通模式部署与时间的关系，但人口增长也是部署的重要驱动因素。通过回归模型直接控制人口或通过测试邮件量或邮局设施与人口的比率来间接控制人口，有助于分离人口和时间的影响。

邮局设施模型最能体现 S 型曲线部署模式。$T<1901$ 的邮局数量增长模型具有较高的 $R^{2}$ 值。控制人口因素增强了回归系数和 $R^{2}$ 值。邮局设施关闭/废弃的衰减模型最好地模拟了向家庭送货的转变，以及随后的技术模式转变。控制人口因素降低了回归系数，但仍提高了 $R^{2}$ 值。