运输经济学/生产

生产

介绍

运输利用各种车辆在不同的基础设施系统上将人员和货物从一个地方移动到另一个地方。它不仅使用技术（即车辆、能源和基础设施），还使用人们的时间和努力；不仅产生乘客出行和货物运输的预期产出，还产生诸如空气污染、噪音、拥堵、碰撞、伤害和死亡等不利结果。

图 1 说明了运输的投入、产出和结果。在左上角是传统的投入（基础设施（包括路面、桥梁等）、生产运输所需的劳动力、基础设施占用的土地、能源投入和车辆）。基础设施是传统土木工程的保留地，而车辆则扎根于机械工程。能源，就其为现有车辆提供动力而言，是一个机械工程问题，但旨在减少或最大限度地减少能源消耗的系统设计需要超越传统的学科界限思考。

在图的顶部是信息、运营和管理以及旅行者的時間和精力。运输系统为人们服务，并由人们创建，包括系统所有者和运营商，他们运营、管理和维护系统，以及使用系统的旅行者。旅行者的時間取决于自由流时间，它是基础设施设计的结果，以及由于拥堵造成的延误，这是系统容量及其使用量的相互作用。在图的右上角是运输的不利结果，尤其是其负外部性

通过污染，系统消耗健康并增加发病率和死亡率；
因为危险，它们消耗安全并造成伤害和死亡；
因为嘈杂，它们消耗安静并产生噪音（降低生活质量和财产价值）；以及
通过排放碳和其他污染物，它们损害环境。

所有这些因素都越来越被认为是运输的成本，但最值得注意的是环境影响，尤其是对全球气候变化的担忧。图的底部显示了运输的产出。运输是经济活动和人们生活的核心，它使他们能够从事工作、上学、购买食物和其他商品，并参与构成人类存在的所有活动。更多的运输，通过增加对更多目的地的可达性，使人们能够更好地满足他们的个人目标，但也意味着更高的个人和社会成本。虽然“运输问题”通常以拥堵的方式提出，但这种延误只是拥有许多成本和更多益处的系统的成本之一。此外，通过改变可达性，运输塑造了土地的开发。

运输与生产

运输是一个生产过程，也是企业、城市、州和国家生产函数中的一个要素投入。运输是由各种服务产生的，并与其他投入一起用于生产经济中的商品和服务。运输是一种中间产品，因此它具有“派生需求”。生产理论可以指导我们思考如何有效地生产运输以及如何有效地利用运输来生产其他商品。

更广泛地说，人们将运输作为投入进入生产过程。例如，国民生产总值（GNP）是衡量产出的指标，它是用资本、劳动力、能源、材料和运输作为投入生产的。GNP = f(K, L, E, M, T)

或者，我们可以将运输视为产出：例如，航空服务的客运里程、货运服务的吨公里或公共汽车的运行里程。这些产出是由包括运输在内的投入产生的。

T = g(K, L, E, M,)

本章将重点介绍后一种观点。

生产过程涉及大量的投入和产出。通常需要对这些投入和产出进行汇总，以便分析更易于管理；例如包括各种类型劳动和各种类型运输。

衡量投入和产出

物质投入 - 体积/质量
人力投入 - 劳动力和用户（時間）
服务投入 - 导航、码头运营
资本投入 - 物理单位、货币单位（存量和流量）
设计投入 - 尺寸、重量、功率
运输 - 货运航程、车辆航程、车辆里程、容量里程、里程

运输生产的特征

在运输中，产出是“服务”，而不是产品。它不可储存（现在未使用的容量不能以后出售，这导致了高峰/非高峰的经济学），用户参与生产（乘客是生产产出的关键因素）。

投入由承运人、用户和公众提供

承运人：码头活动、干线活动等。
用户：时间价值等。
公众：基础设施

生产的特点是多维（异构）产出。

数量：最常见的产出衡量指标；
- 吨公里
- 客运公里
空间维度 - 起点-终点和方向
時間维度 - 运输时间、高峰和季节性
服务质量 - 速度、可靠性等。

以下表格说明了在考虑投入和产出时使用生产方法进行系统设计的示例

投入	产出
维度	表面积/体积承载能力
尺寸、速度	运输能力（例如，每小时车辆数）
系统容量、基础设施质量	交通流量
容量、车辆移动	O-D 航程
跑道、航站楼	乘客和飞机的移动

大块投资是指投资的不可分割性导致复杂的成本核算和定价。例如，您不能建造半条车道或半条跑道，然后使其变得有用。

沉没投资可能构成进入壁垒。

联合生产是指不可避免地以固定比例生产多种产出，例如，正向运输-反向运输问题；存在联合成本分配问题。联合成本是指多种产品以固定不变的比例存在。

在共同生产中，使用相同设备或设施生产比例不同的多种产出 - 节省成本的优势，例如，货运和客运服务使用同一架飞机，或使用同一列火车。共同成本是指多种服务可以以可变比例生产，而成本支出相同

承运人有一个结构，可以分解为两个主要活动（码头和干线）

码头活动包括货物的装卸和分拣（以及可能包括提货和送货）。速度的概念对于码头来说可能很重要，而要行驶的距离则与之关系不大。码头活动可能因货物类型而异，例如，我们看到散装装卸设施的规模收益递增，但对于处理各种产品类型的设施而言，规模收益递增是否明显尚不清楚。

干线活动表现出由于以下原因导致供给方产出单位的不可分割性

容量块和产出不可储存性（需求和生产数量之间的不匹配）
反向运输能力的联合生产
共同生产；例如，短途市场与长途市场一起服务。

生产理论

生产理论分析了企业如何在给定技术的情况下，将投入（ $x$ ）转化为产出（ $y$ ），以经济有效的方式。生产函数， $y=f(x)$ ，用于描述产出与投入之间的关系。

效率

X效率是指使用给定投入组合生产产出的效率。如果企业在雇佣资源的情况下能够生产出最大产出，那么它就是X效率的。

配置效率是指资源配置以最大限度地实现资源使用带来的净收益的市场状态。在这种市场状态下，不可能让一个人变得更好，而不会让另一个人变得更糟。

技术效率是指用最少的投入生产给定产出的能力，或者等效地，在生产边界上运行而不是在其内部运行。

生产可能性集

生产可能性集是投入和产出可行组合的集合。例如，为了生产一定数量的客运量，飞机可以经常加油，从而减少油量，或者减少加油次数，并增加油量。产出是车辆行驶量，投入是燃油和劳动力。

如果生产可能性集 (PPS) 是凸的，那么可以根据单个条件识别出最佳投入组合。但是，如果 PPS 不是凸的，那么标准就会变得模棱两可。我们需要查看整个等产量曲线才能找到最佳值，但在没有凸性的情况下，我们会变得“近视”，如右侧所示。

投入价格的线性齐次性

$C\left(Q,2P_{1},2P_{2}\right)=2C\left(Q,P_{1},P_{2}\right)$

所有产出的边际成本都为正

${\frac {\partial C}{\partial Q_{j}}}>0\forall j$ .

成本函数对投入价格的导数产生投入需求函数。

${\frac {\partial C}{\partial P_{j}}}=X\left(\bullet \right)$

随着投入价格的上升，我们总是会从相对更昂贵的投入中进行替代。

${\frac {\partial ^{2}C}{\partial P_{i}^{2}}}\leq 0\forall i$

函数形式

生产函数是在给定技术的情况下，投入和产出之间的关系。技术的变化可以影响生产函数，主要体现在两个方面。首先，它会改变产出水平，因为它会影响所有投入，其次，它会通过改变投入组合来提高产出。大多数生产函数是在技术保持不变的假设下估计的。这类似于在估计需求关系时假设消费者偏好保持不变或不变。

函数形式表示投入的组合方式。这些形式可以从简单的线性或对数线性（柯布-道格拉斯）关系到以“对数函数”表示的二阶近似。

线性

线性生产函数是最简单的

Y=A+\alpha L+\beta K

二次方程

二次生产函数增加了平方项和交互项。

Y=A+\alpha L+\beta K+\gamma L^{2}+\phi K^{2}+\rho KL

柯布-道格拉斯

(改编自维基百科关于柯布道格拉斯函数的文章 )

对于生产，柯布-道格拉斯函数是

Y=AL^{\alpha }K^{\beta },

其中

Y = 总产量（一年内生产的所有商品的货币价值）
L = 劳动力投入
K = 资本投入
A = 全要素生产率
$\alpha$ 和 $\beta$ 分别是产出弹性，分别代表劳动力和资本。这些值是由可用技术决定的常数。

产出弹性衡量的是产出对生产中使用劳动力或资本水平变化的响应程度，在其他条件不变的情况下。例如，如果 $\alpha =0.15$ ，劳动力增长 1% 将导致产出大约增长 0.15%。

此外，如果

\alpha +\beta =1

生产函数具有规模报酬不变。也就是说，如果 L 和 K 都增加 20%，Y 将增加 20%。如果

\alpha +\beta <1

规模报酬递减，如果

\alpha +\beta >1

规模报酬递增。假设完全竞争和 $\alpha +\beta =1$ ， $\alpha$ 和 $\beta$ 可以证明是劳动力和资本在产出中的份额。

Translog

Translog 生产函数是柯布-道格拉斯生产函数的推广。Translog 代表“超越对数”。

双要素 Translog 生产函数是

{\begin{aligned}\ln(Y)&=\ln(A)+a_{L}\ln(L)+a_{K}\ln(K)+b_{LL}\ln(L)\ln(L)\\&{}\qquad {}+b_{KK}\ln(K)\ln(K)+b_{LK}\ln(L)\ln(K)\\&=f(L,K).\end{aligned}}

其中 L = 劳动力，K = 资本，Y = 产品。

CES（替代弹性恒定）

替代弹性恒定（CES）函数： $Y=A[\alpha K^{\gamma }+(1-\alpha )L^{\gamma }]^{\frac {1}{\gamma }}$

$\gamma =0$ 对应于科布-道格拉斯函数， $Y=AK^{\alpha }L^{1-\alpha }$

列昂惕夫

该列昂惕夫生产函数适用于投入必须以固定比例使用的场合；从这些比例开始，如果增加一种投入的使用量而另一种投入的使用量没有增加，产出将不会发生变化。该生产函数由以下公式给出：

Y=\min(aK,\ \ bL,\ \ ...).

生产函数的特征

生产关系的考察需要理解生产函数的性质。考虑将产出与两个投入联系起来的一般生产函数（这里只用两个投入是为了说明方便，结论在考虑更多投入或产出时不会改变，只是更复杂而已）

$Q=f(K,L)$

考虑将资本量固定在某个水平上，并考察在增加劳动力（可变要素）投入量时产出的变化。我们对 $\Delta Q/\Delta L$ 感兴趣，它被定义为劳动力的边际产量，以及 $Q/L$ 劳动的平均产量。对于任何投入，都可以定义这些，劳动只是用作示例。

这表示一个“普通”的生产函数。这描述了一个短期关系。它是短期，因为至少一个投入是固定的。考察在一种投入变化时产出的行为是有指导意义的。

请注意，平均产量 (AP) 上升并达到最大值，在该点，射线的斜率 $Q/L$ 达到最大值，然后渐近递减。

边际产量 (MP) 上升（边际生产率上升区域），在 AP 上方，并达到最大值。它下降（边际生产率下降区域），并在 AP 的最大值处与 AP 相交。当总产量 (TP) 达到最大值时，MP 降至零。应该清楚为什么使用 AP 作为生产力指标（政府、行业、工程师等经常使用的指标）是非常可疑的。例如，在 $MP=0$ 之后， $AP>0$ ，但 TP 正在下降。

这里的“边际生产率递减原理”得到了很好的体现。该原理指出，当你在固定要素中添加可变要素的单位时，最初产量将上升，而且很可能以越来越快的速度上升（但不一定），但在某个时刻，添加更多可变投入将对总产出的贡献越来越少，最终可能导致总产出下降（同样不一定）。

固定要素（或技术）的任何变化都会导致 TP、AP 和 MP 函数向上移动。这提出了一个有趣且重要的议题，即是什么产生了产出的变化；可变要素的变化、技术的变化，或者技术的变化。

等产量曲线

等产量曲线揭示了关于技术和替代性的很多信息。与无差异曲线类似，等产量曲线的曲率表示两种要素之间的替代程度。它们越“直角化”，替代程度越低。此外，边际产量递减在等产量曲线的斜率中起作用，因为随着要素比例的变化，相对边际产量的变化。因此，替代性不仅仅是生产技术的问题，也是投入的相对比例的问题。

与其考虑一个可变要素，不如考虑两个（或所有）可变要素。

$Q=f(K,L)$ .

取全微分并令其等于零

$dQ={\frac {\partial f}{\partial K}}dK+{\frac {\partial f}{\partial L}}dL=0$

重新排列可以看出，边际生产率之比 ( ${\frac {MP_{K}}{MP_{L}}}$ ) 等于 ${\frac {dk}{dL}}$

等价地，等产量曲线是K 和 L 组合的轨迹，这些组合将产生相同的产量水平，并且等产量曲线的斜率（ ${\frac {dk}{dL}}$ ）等于边际产量之比。

边际产出之比也称为“技术替代边际率”MRTS。

当从原点向外移动时，产量水平会上升，但与无差异曲线不同，等产量曲线是可以进行基数度量的。它们之间的距离将反映生产技术的特征。

等产量曲线模型可以用来说明寻找以最低成本生产给定产量的解决方案，或者等价地，从给定预算中获得最大产量的解决方案。最里面的预算线对应于与预算线相交的投入价格，最佳数量是最佳成本与预算线交点处的坐标。该解决方案可以是内部解决方案或角点解决方案，如下面的图表所示。

约束优化

这个刚刚说明的约束优化问题的例子是

${\begin{aligned}&{\text{Min cost }}={\text{ }}p_{1}x_{1}+p_{2}x_{2}\\&{\text{s}}{\text{.t}}{\text{. }}F(x_{1},x_{2})=Q\\\end{aligned}}$

其中

f() 是生产函数
目标函数（最小成本）：愿望
约束（受制于）：必要性
$x_{1},x_{2}$ : 决策变量

拉格朗日乘子法是一种通过引入额外的决策变量将约束问题转化为无约束问题的方法。这些“新的”决策变量具有有趣的经济解释。

${\begin{aligned}&{\text{Max }}g\left({\bar {x}}\right)\\&{\text{s}}{\text{.t}}{\text{. }}h_{j}\left({\bar {x}}\right)=b_{j}\\\end{aligned}}$

拉格朗日函数

${\text{Max}}\Lambda \left({\bar {x}},{\bar {\lambda }}\right)=g\left({\bar {x}}\right)-\sum {{\bar {\lambda }}_{j}\left(h_{j}\left({\bar {x}}\right)-b_{j}\right)}$

为了找到最大值，取一阶导数并将其设置为零

${\frac {\partial \Lambda }{\partial x_{i}}}={\frac {\partial g}{\partial x_{i}}}-\sum \limits _{j}{\lambda _{j}}{\frac {\partial h_{j}}{\partial x_{i}}}=0$

${\frac {\partial \Lambda }{\partial \lambda _{j}}}=-h_{j}\left(x\right)+b_{j}=0$

拉格朗日函数被最大化（最小化）
拉格朗日函数等于原始目标函数
约束条件得到满足

拉格朗日乘子代表如果约束条件发生变化，目标函数将发生变化的幅度。因此，例如，当与生产函数一起使用时，拉格朗日函数将被解释为预算约束的“影子价格”，即如果预算增加一个单位，产量可以增加的幅度，或者等价地，增加一个单位产量的边际成本。

示例

${\begin{aligned}&{\text{Min cost }}={\text{ }}p_{1}x_{1}+p_{2}x_{2}\\&{\text{s}}{\text{.t}}{\text{. }}F(x_{1},x_{2})=Q\\\end{aligned}}$

$\Lambda =p_{1}x_{1}+p_{2}x_{2}-\lambda (F(x_{1},x_{2})-Q)$

${\frac {\partial \Lambda }{\partial x_{1}}}=-p_{\text{1}}-\lambda {\frac {\partial F\left(x_{\text{1}},x_{\text{2}}\right)}{\partial x_{\text{1}}}}=0$

${\frac {\partial \Lambda }{\partial x_{2}}}=-p_{\text{2}}-\lambda {\frac {\partial F\left(x_{\text{1}},x_{\text{2}}\right)}{\partial x_{\text{2}}}}=0$

${\frac {\partial \Lambda }{\partial \lambda _{j}}}=Q-F\left(x_{\text{1}},x_{\text{2}}\right)=0$

${\frac {p_{\text{1}}}{\frac {\partial F\left(x_{\text{1}},x_{\text{2}}\right)}{\partial x_{\text{1}}}}}=\lambda$

${\frac {p_{2}}{\frac {\partial F\left(x_{\text{1}},x_{\text{2}}\right)}{\partial x_{2}}}}=\lambda$

${\frac {p_{\text{1}}}{p_{2}}}={\frac {\frac {\partial F\left(x_{\text{1}},x_{\text{2}}\right)}{\partial x_{\text{1}}}}{\frac {\partial F\left(x_{\text{1}},x_{\text{2}}\right)}{\partial x_{2}}}}$

所以

$\lambda ={\frac {\partial \Lambda }{\partial Q}}$

等于边际产出成本。

条件

一阶条件（FOC）不足以定义最小值或最大值。

二阶条件也是必需的。然而，如果生产集是凸的，并且投入成本函数是线性的，那么FOC足以定义最大产出或最小成本。

优化

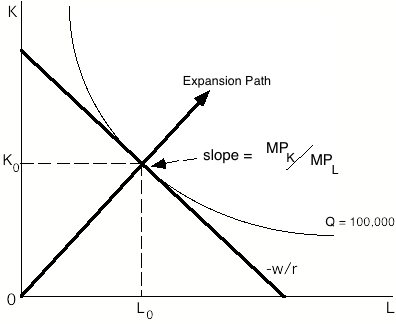
利润最大化的公司将雇用要素，直到这些要素对收入的贡献等于对成本的贡献为止。等产量曲线有助于说明这一点。

考虑一家利润最大化的公司，以及它选择最优要素组合的决定。

$\Pi =Pf\left(K,L\right)-\left(wL+rK\right)$

${\frac {\partial \Pi }{\partial K}}=P{\frac {\partial f}{\partial K}}-r=0$

${\frac {\partial \Pi }{\partial L}}=P{\frac {\partial f}{\partial L}}-w=0$

这表明，利润最大化的公司将雇用生产要素，直到它们对收入的贡献（边际收益产品）或产品价格乘以生产要素的边际产量等于它们对公司的成本贡献。这个解决方案可以通过等产量图来说明。

均衡点，即最佳投入组合，是指公司可以将一种投入与另一种投入之间进行交易的比率（由技术决定的），正好等于市场允许您将一种生产要素与另一种生产要素之间进行交易的比率（由相对工资率决定的）。这个均衡点应该被认为等同于成本函数上的一个点。请注意，这在原则上与需求中的效用空间和产出空间相同。它还指出了一个可能影响成本的重要因素；即您是否处于扩张路径上。

为了从生产函数转换到成本函数，我们需要找到投入成本最小化的投入组合来生产给定的产出。我们已经看到，这就是扩张路径。因此，从生产函数到成本函数的转换需要三个关系

生产函数
预算约束
扩张路径

“生产成本函数”是指生产给定产出可能的最低成本。

对偶性

生产函数和成本函数之间存在着对偶关系。这意味着生产函数中包含的所有信息也包含在成本函数中，反之亦然。因此，正如从消费者支出信息中可以恢复偏好映射一样，也可以从成本函数中恢复生产函数。

假设我们知道成本函数 C(Q,P')，其中 P" 是投入价格向量。如果我们让产出和投入价格取值 C˚, P˚1 和 P˚2，我们可以推导出生产函数。

1. 了解产出水平和投入价格的具体值意味着我们知道最佳投入组合，因为等产量曲线的斜率等于相对价格的比率。

2. 了解等产量曲线的斜率意味着我们知道预算线的斜率

3. 我们知道产出水平。

因此，我们可以针对我们想要的任何 Q 和 P 值生成类似的陈述，因此可以绘制完整的等产量图，除了不是最佳投入组合的投入组合。

要素需求函数

从生产分析中得出的一个重要概念是，对生产要素的需求是派生需求；也就是说，人们不需要它本身，而是为了它能生产的东西。对生产要素的需求函数是从其边际产量曲线得出的，事实上，要素需求曲线是边际产量曲线中位于平均产量曲线以下的部分。随着要素使用量的增加，边际产量将下降，因此沿着要素需求曲线下降。如果生产要素用于生产的产品的价格发生变化，要素需求函数将发生移动。同样，技术进步将导致边际产量曲线发生移动。

投入成本函数

回想一下，我们的生产函数 Q = f(x1, x2) 可以转换为成本函数，因此我们从投入空间转移到美元空间。生产函数是一个技术关系，而成本函数不仅包括技术，还包括优化行为。

转换需要一个预算约束或投入价格。将存在可行的非最佳投入组合，这些组合可以产生给定的产出，以及可行的最佳投入组合，这些组合可以产生最佳解决方案。

技术变革

技术变革可以以三种基本形式进入生产函数；长期、创新和设施或基础设施。

技术变革可以影响生产函数中的所有生产要素，从而成为“要素中性”，或者它可能对生产要素的影响不同，在这种情况下它将是“要素偏向”。

技术变革的结果是使生产函数向上移动（或等效地，正如我们将看到的，使成本函数向下移动），它也可以改变生产函数的形状，因为它可能会改变生产要素组合。

这可以用等产量图来表示，如右侧所示。

如果相对生产要素价格没有发生变化，那么技术变革可能不会导致新的扩张路径，如果技术变革是要素中性的，那么它只会使生产函数向上平行移动。如果技术变革不是要素中性的，那么等产量曲线将改变形状，因为生产要素的边际产量将发生变化，因此将出现新的扩张路径。

技术变革类型

长期 - 包括生产函数中的时间
创新 - 包括生产函数中的创新存在
设施 - 包括生产函数中设施的可用性

条件

一阶条件（FOC）不足以定义最小值或最大值。

二阶条件也是必需的。然而，如果生产集是凸的，并且投入成本函数是线性的，那么FOC足以定义最大产出或最小成本。

参考文献

供应链	运输经济学	成本
	生产