交通地理与网络科学/图论

改编自维基百科文章[1]
图论是研究图,一种用于对来自特定集合的对象之间的成对关系进行建模的数学结构。在此上下文中,“图”指的是一组顶点或“节点”以及连接顶点对的一组边。图可以是无向的,这意味着与每条边关联的两个顶点之间没有区别,或者它的边可以有向地从一个顶点指向另一个顶点;请参阅此处以了解更详细的定义以及其他常用图类型的变化。
请参考此处以了解图论中的基本定义。
图是自然和人造结构中最普遍的模型之一。它们可用于对物理、生物和社会系统中的许多关系和过程动态进行建模。许多实际应用问题可以用图来表示。
在计算机科学中,图用于表示通信网络、数据组织、计算设备、计算流程等。一个实际例子:网站的链接结构可以用有向图来表示。顶点是网站上可用的网页,如果且仅当页面A包含指向页面B的链接时,从页面A到页面B才存在有向边。类似的方法可以应用于交通、生物学、计算机芯片设计以及其他许多领域的问题。因此,开发处理图的算法是计算机科学中的一个重要领域。在那里,图的转换通常被形式化并通过图重写系统来表示。它们要么被直接使用,要么研究重写系统的属性(例如汇合)。作为侧重于基于规则的图内存操作的图转换系统,图数据库侧重于对图结构化数据的交易安全、持久存储和查询。
图论方法以各种形式在语言学中已被证明特别有用,因为自然语言通常非常适合离散结构。传统上,句法和组合语义遵循基于树的结构,其表达能力在于组合原理,在分层图中建模。在词汇语义中,特别是应用于计算机时,当在相关词语的意义上理解给定词语时,对词语意义进行建模更容易;因此,语义网络在计算语言学中很重要。在音系学(例如,最优性理论,使用格图)和形态学(例如,有限状态形态学,使用有限状态转换器)中,还有其他方法在将语言分析为图时很常见。事实上,这个数学领域对语言学的用处已经产生了像TextGraphs这样的组织,以及各种“Net”项目,如WordNet、VerbNet等等。
图论也被用于研究化学和物理学中的分子。在凝聚态物理学中,可以通过收集与原子拓扑结构相关的图论属性的统计信息来定量研究复杂模拟原子结构的三维结构。例如,Franzblau 的最短路径 (SP) 环。在化学中,图对分子构成一个自然的模型,其中顶点代表原子,边代表键。这种方法特别用于分子结构的计算机处理,从化学编辑器到数据库搜索。在统计物理学中,图可以表示相互作用系统各个部分之间的局部连接,以及这些系统上物理过程的动力学。
图论在社会学中也得到了广泛应用,例如,用它来衡量演员的声望或探索w:扩散机制,特别是通过使用w:社会网络分析软件。
同样,图论在w:生物学和保护工作中也很有用,其中顶点可以代表某些物种存在(或栖息地)的区域,边代表迁徙路径或区域之间的移动。当查看繁殖模式或跟踪疾病、寄生虫的传播或运动变化如何影响其他物种时,这些信息非常重要。
在数学中,图在几何学和拓扑学的某些部分很有用,例如纽结理论。代数图论与群论有着密切的联系。
可以通过为图的每条边分配一个权重来扩展图结构。带有权重的图,或w:带权图,用于表示成对连接具有某些数值的结构。例如,如果图表示一个道路网络,权重可以代表每条道路的长度。
在图论中,带有加权边的有向图被称为网络。网络分析具有许多实际应用,例如,对交通网络进行建模和分析。网络分析的应用大体分为三类
- 首先,分析以确定网络的结构属性,例如顶点度数的分布和图的直径。存在大量图度量,针对不同领域产生有用的度量仍然是研究的活跃领域。
- 其次,分析以在网络中找到可衡量的量,例如,对于交通网络,任何部分的车辆流量水平。
- 第三,分析网络的动力学属性。
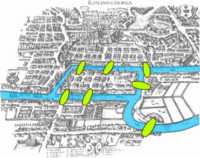
莱昂哈德·欧拉关于w:哥尼斯堡七桥问题的论文写于 1736 年,被认为是图论历史上第一篇论文。[1] 这篇论文以及范德蒙德关于骑士巡游问题的论文,延续了莱布尼茨发起的位相分析。欧拉关于凸多面体的边数、顶点数和面数之间的关系的公式由柯西[2]和L'Huillier[3]研究和推广,是w:拓扑学的起源。
欧拉关于 w:柯尼斯堡 桥梁的论文发表一个多世纪后,虽然 李斯廷 引入了拓扑学,但 凯莱 从 w:微积分 中出现的特定解析形式的研究中,开始研究一类特定的图,即树。这项研究对理论 w:化学 产生了诸多影响。所涉及的技术主要与 w:图的枚举 具有特定性质的图有关。枚举图论由此起源于凯莱的研究成果,以及 波利亚 在 1935 年至 1937 年间发表的基础成果,以及 德布鲁因 在 1959 年对这些成果的推广。凯莱将他在树方面的成果与当时对化学成分的研究联系起来。[4] 数学思想与化学思想的融合是图论标准术语的一部分的起源。
特别是,“图”这个词是由 西尔维斯特 在 1878 年发表在自然上的一篇论文中提出的,他在论文中将代数的“量子不变量”和“共变数”与分子图进行了类比:[5]
- “[...] 因此,每个不变量和共变数都可以用一个图来表示,该图与 凯库勒 图或化学图完全相同。[...] 我给出图形几何乘法的规则,即,如何为已知单独图形的不变量或共变数的乘积构造一个图形。[...]”(斜体与原文一致)。
图论中最著名、最有成效的问题之一是 w:四色问题:“是否真的任何绘制在平面上的地图都可以用四种颜色对它的区域进行着色,使得任何两个具有共同边界的区域都具有不同的颜色?”这个问题最早是由 w:弗朗西斯·格思里 于 1852 年提出的,其第一个书面记录是在 德·摩根 写给 哈密尔顿 的信中,时间为同年。许多不正确的证明被提出,包括凯莱、肯普 以及其他人的证明。对这个问题的研究和推广,由 泰特、希伍德、拉姆齐 和 哈德维格 完成,这导致了对嵌入在具有任意 亏格 的曲面上的图的着色的研究。泰特的重新表述产生了一类新的问题,即分解问题,这些问题由 彼得森 和 柯尼格 研究。拉姆齐关于着色的研究,更具体地说,图兰 在 1941 年取得的成果是图论另一个分支的起源,即w:极图论。
四色问题在一个多世纪的时间里一直没有得到解决。1969 年,w:海因里希·希施 发表了一种使用计算机解决该问题的方法。[6] 1976 年,w:肯尼斯·阿佩尔 和 w:沃尔夫冈·哈肯 给出了一個计算机辅助证明,该证明利用了希施提出的“放电”的概念。[7][8] 该证明涉及通过计算机检查 1,936 种配置的属性,并且由于其复杂性,当时并没有完全被接受。20 年后,罗伯逊、西摩、桑德斯 和 托马斯 给出了一个更简单的证明,该证明只考虑了 633 种配置。[9]
拓扑学从 1860 年到 1930 年的自主发展,通过 若尔当、库拉托夫斯基 和 惠特尼 的作品,使图论重新焕发活力。图论和拓扑学共同发展另一个重要因素来自于现代代数技术的应用。第一个此类应用的例子来自物理学家 w:古斯塔夫·基尔霍夫 的工作,他在 1845 年发表了计算 w:电路 中 w:电压 和 电流 的 w:基尔霍夫电路定律。
在图论中,特别是 埃尔德什 和 雷尼 关于图连通性的渐进概率的研究中引入了概率方法,这催生了另一个分支,称为随机图论,它一直是图论结果的一个富有成效的来源。
绘制图形
[edit | edit source]通过为每个顶点绘制一个点或圆圈,并在两个顶点之间绘制一条弧线(如果它们由一条边连接)来图形地表示图。如果图是有向的,则通过绘制箭头来指示方向。
不应将图的绘制与图本身(抽象的、非视觉结构)混淆,因为图的绘制有多种方式。重要的是哪些顶点通过多少条边连接到哪些其他顶点,而不是确切的布局。实际上,很难决定两个图是否代表同一个图。根据问题域,一些布局可能比其他布局更适合,更容易理解。
图论数据结构
[edit | edit source]在计算机系统中存储图的方法有很多。使用的 w:数据结构 取决于图的结构以及用于操作图的 w:算法。从理论上讲,可以区分列表结构和矩阵结构,但在具体应用中,最佳结构通常是两者的组合。列表结构通常更适合 w:稀疏图,因为它们具有较小的内存需求。另一方面,矩阵结构为某些应用程序提供了更快的访问速度,但可能会消耗大量内存。
列表结构
[edit | edit source]- w:关联列表
- 边用一个包含顶点对(如果是带方向的,则为 w:元组)的 数组 来表示(边连接的顶点),并可能包含权重和其他数据。由一条边连接的顶点被称为相邻的。
- w:邻接列表
- 与关联列表非常相似,每个顶点都有一个列表,列出它与哪些顶点相邻。这会在无向图中导致冗余:例如,如果顶点 A 和 B 相邻,则 A 的邻接列表包含 B,而 B 的列表包含 A。邻接查询速度更快,但需要额外的存储空间。
矩阵结构
[edit | edit source]- w:关联矩阵
- 图用一个大小为 |V |(顶点数)乘以 |E|(边数)的 矩阵 来表示,其中条目 [顶点,边] 包含边的端点数据(最简单的情况:1 - 相邻,0 - 不相邻)。
- w:邻接矩阵
- 这是一个n 乘以n 的矩阵A,其中n 是图中顶点的数量。如果从顶点x 到顶点y 有一条边,则元素 为 1(或者更一般地,为xy 边数),否则为 0。在计算中,这个矩阵使得很容易找到子图,以及反转有向图。
- w:拉普拉斯矩阵 或 w:基尔霍夫矩阵 或导纳矩阵
- 它被定义为 D − A,其中 D 是对角线 w:度矩阵。它显式地包含邻接信息和度信息。(然而,还有其他类似的矩阵也称为图的“拉普拉斯矩阵”。)
- w:距离矩阵
- 一个对称的 n 乘 n 矩阵 D,它的元素 是 x 和 y 之间 w:最短路径 的长度;如果不存在这样的路径,则 = 无穷大。它可以从 A 的幂推导出。
关于 w:图形枚举 存在大量的文献:计数满足指定条件的图形的问题。其中一些工作可以在 Harary 和 Palmer(1973)中找到。
一个常见的问题,称为 w:子图同构问题,是在给定图中找到一个固定图作为 w:子图。对这个问题感兴趣的原因之一是,许多 w:图属性 对于子图是 遗传的,这意味着一个图具有该属性当且仅当它的所有子图也具有该属性。不幸的是,找到某种类型的最大子图通常是一个 w:NP 完全问题。
一个类似的问题是找到给定图中的 w:导出子图。同样地,一些重要的图属性对于导出子图是遗传的,这意味着一个图具有该属性当且仅当它的所有导出子图也具有该属性。找到某种类型的最大导出子图也通常是 NP 完全的。例如,
另一个类似的问题,即 次图包含问题,是在给定图中找到一个固定图作为次图。一个图的 次图 或 子收缩图 是通过取一个子图并收缩一些(或没有)边而获得的任何图。许多图属性对于次图是遗传的,这意味着一个图具有该属性当且仅当它的所有次图也具有该属性。一个著名的例子
另一类问题与各种物种和图的推广在多大程度上由它们的 点删除子图 决定有关,例如
- The w:重建猜想
许多问题与 图着色 的各种方法有关,例如
- The w:四色定理
- The 强完美图定理
- The w:Erdős–Faber–Lovász 猜想(未解决)
- The 总着色猜想(未解决)
- The 列表边着色猜想(未解决)
- The w:Hadwiger 猜想(图论)(未解决)
- 哈密顿路径和循环问题
- w:最小生成树
- w:路线检查问题(也称为“中国邮递员问题”)
- w:哥尼斯堡七桥问题
- w:最短路径问题
- w:施泰纳树
- w:三间小屋问题
- w:旅行商问题(NP 完全)
许多问题特别是来自与 网络流 的各种概念相关的应用,例如
覆盖问题 是子图查找问题的一些特定实例,它们往往与 w:团问题 或 w:独立集问题 紧密相关。
许多问题涉及到对各种图类的成员进行特征化。这种类型的问题与本列表中的其他类型有很大的重叠,例如
- w:图属性
- w:代数图论
- w:概念图
- w:数据结构
- w:不相交集数据结构
- w:实体图
- w:存在图
- 图数据结构
- w:图代数
- w:图自同构
- w:图着色
- w:图数据库
- w:图绘制
- w:图方程
- w:图重写
- w:图夹心问题
- w:交集图
- w:逻辑图
- 循环
- w:零图
- w:卵石运动问题
- w:完美图
- w:量子图
- w:谱图论
- w:强正则图
- w:对称图
- 树数据结构
- w:Bellman-Ford 算法
- w:Dijkstra 算法
- w:Ford-Fulkerson 算法
- w:Kruskal 算法
- w:最近邻算法
- w:Prim 算法
- w:深度优先搜索
- w:广度优先搜索
- Berge, Claude
- Bollobás, Béla
- Chung, Fan
- Dirac, Gabriel Andrew
- Erdős, Paul
- Euler, Leonhard
- Faudree, Ralph
- Golumbic, Martin
- Graham, Ronald
- Harary, Frank
- Heawood, Percy John
- Kőnig, Dénes
- Lovász, László
- Nešetřil, Jaroslav
- Rényi, Alfréd
- Ringel, Gerhard
- Robertson, Neil
- Seymour, Paul
- Szemerédi, Endre
- Thomas, Robin
- Thomassen, Carsten
- Turán, Pál
- Tutte, W. T.
- ↑ Biggs, N.; Lloyd, E. 和 Wilson, R. (1986), 图论,1736-1936, 牛津大学出版社
{{citation}}: CS1 maint: multiple names: 作者列表 (link) - ↑ Cauchy, A.L. (1813), "关于多面体的研究 - 第一篇论文", 理工学院杂志, 9 (Cahier 16): 66–86.
- ↑ L'Huillier, S.-A.-J. (1861), "关于多面体的论文", 数学年鉴, 3: 169–189.
- ↑ Cayley, A. (1875), "关于在数学中被称为树的解析图形及其在化学键理论中的应用", 德国化学学会通讯, 8: 1056–1059, doi:10.1002/cber.18750080252.
- ↑ John Joseph Sylvester (1878), 化学与代数. 自然,第 17 卷,第 284 页。 doi:10.1038/017284a0. 在线版本. 2009-12-30 检索.
- ↑ Heinrich Heesch: 关于四色问题的研究. 曼海姆: 文献研究所 1969.
- ↑ Appel, K. 和 Haken, W. (1977), "每个平面地图都是四色的。第一部分。放电", 伊利诺伊州数学杂志, 21: 429–490.
{{citation}}: CS1 maint: 多个名称: 作者列表 (link) - ↑ Appel, K. 和 Haken, W. (1977), “每张平面图都是四色的。第二部分:可约性”,伊利诺伊州数学杂志,21: 491–567。
{{citation}}: CS1 maint: 多个名字:作者列表 (link) - ↑ Robertson, N.;Sanders, D.;Seymour, P. 和 Thomas, R. (1997), “四色定理”,组合理论杂志 B 系列,70: 2–44,doi:10.1006/jctb.1997.1750.
{{citation}}: CS1 maint: 多个名字:作者列表 (link)
参考文献
[edit | edit source]- Berge, Claude (1958), 图论及其应用,大学数学丛书,卷。 II,巴黎:Dunod。英语版,Wiley 1961 年;Methuen & Co,纽约 1962 年;俄语,莫斯科 1961 年;西班牙语,墨西哥 1962 年;罗马尼亚语,布加勒斯特 1969 年;中文,上海 1963 年;1962 年第一版英语版的第二次印刷,Dover,纽约 2001 年。
- Biggs, N.;Lloyd, E.;Wilson, R. (1986), 图论,1736–1936,牛津大学出版社.
- Bondy, J.A.;Murty, U.S.R. (2008), 图论,施普林格,ISBN 978-1-84628-969-9.
- Chartrand, Gary (1985), 图论导论,Dover,ISBN 0-486-24775-9.
- Gibbons, Alan (1985), 算法图论,剑桥大学出版社.
- Golumbic, Martin (1980), 算法图论与完美图,学术出版社.
- Harary, Frank (1969), 图论,马萨诸塞州雷丁:Addison-Wesley.
- Harary, Frank;Palmer, Edgar M. (1973), 图形枚举,纽约,纽约:学术出版社.
- Mahadev, N.V.R.;Peled, Uri N. (1995), 阈值图及相关主题,北荷兰.
外部链接
[edit | edit source]在线教科书
[edit | edit source]- 图论及其应用 (1976) 作者:Bondy 和 Murty
- 组合优化问题中的相变,第 3 节:图论导论 (2006) 作者:Hartmann 和 Weigt
- 有向图:理论算法及应用 2007 作者:Jorgen Bang-Jensen 和 Gregory Gutin
- 图论,作者:Reinhard Diestel



![{\displaystyle d_{x,y}=\min\{n\mid A^{n}[x,y]\neq 0\}.\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f506de0d11f5bd6d7b97b81eb0348e815c40ac27)

