交通地理与网络科学/网络增长模型

背景

克里斯塔勒（1933）根据交通的经济原理考察了中心地的形成，他指出，“人口的需求、运输成本、投资资本的成本等等，决定性地影响着交通系统的形成”。交通网络和土地利用是城市形态相互依存的塑造者。首先，土地利用的变化改变了出行需求模式。其次，交通流量的增加促使官员通过扩大交通设施来做出回应。第三，新的交通设施改变了可达性模式，这推动了活动的选址和出行行为。

生命周期模型

生命周期模型预测了特定时间点上技术部署的份额。

${\frac {f}{1-f}}=e^{at+b}$

其中： $f$ = 技术的份额（技术在最终市场份额中的份额） $t$ = 时间 $a,b$ = 模型参数

关于交通网络增长的文献并不多。一些研究人员考虑了对网络结构进行建模的问题。Taaffe 等人（1963）研究了道路如何在发展中国家从港口出现，Garrison 和 Marble（1965）考虑了爱尔兰铁路中链接的建设顺序，Helbing 等人（1997）采用了 Lam 和 Pochy（1993）的主动步行者模型，允许在景观上移动的步行者改变景观，Watts 和 Strogatz（1998）提出了小世界模型，Barabasi 等人（1999a，b）建议偏好连接，以便已经连接的节点获得更多连接，这解释了枢纽，而 Yamins 等人（2003）将道路与城市聚落共同进化。

经验模型

还进行了一系列研究，估计现有交通设施扩展和新建链接建设的经验模型（Levinson 和 Karamalaputi 2003a，b）。

基于代理的模型

几篇论文开发了基于代理的模型（使用链接代理）来处理具有固定或随机土地利用模式的网络元素的组织、增长和收缩（Yerra 和 Levinson 2004，Levinson 和 Yerra 2005）。这些模型在一系列论文中得到了扩展（收集在 Xie 和 Levinson 2011 中），放宽了固定网络拓扑、完全分散的代理和缺乏拥堵的假设。

网络增长系统 (SONG) 模型

SONG 模型可以在 [1] 访问。

概述

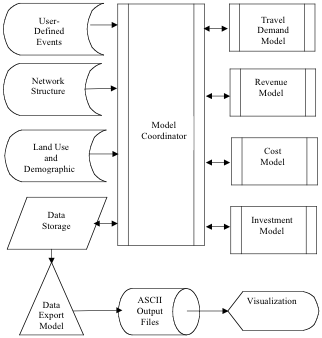
网络增长系统 (SONG) 模型的组成部分包括出行需求、收益、成本和投资。出行需求模型使用给定的网络拓扑将人口和就业数据转换为交通流量，并通过遵循传统的规划步骤（出行产生、出行分配和交通分配）来确定链接流量（为简化起见，假设单一模式）。收益模型根据链接的速度、流量和长度来确定交通流量使用道路必须支付的价格。在下面的实验中，链接长度是固定的，因此收益与链接长度无关，但是，与模型中的所有假设一样，这个假设也可以放宽。成本模型根据交通流量计算维持链接速度所需的成本。超过维护成本的收益将根据投资模型投资于链接以改善其状况，直到所有收益都被消耗掉。在升级（或降级）网络中的每个链接后，时间段会递增，整个过程会重复，直到达到平衡，或者很明显无法实现平衡。图 1 显示了这些模型的概述和相互连接。

复杂系统由许多自治代理组成，它们的相互作用导致系统属性不同于代理属性（单个链接的速度无法告诉你道路的存在，一条道路本身并不表明道路等级（有不同的高速公路、信号灯化的主干道、本地街道）的存在。等级描述了特定网络元素与同一类型其他元素的规模。将交通网络建模为复杂系统涉及对节点（充当交叉路口以及传统出行需求文献中被认为是交通区域中心的节点）、链接（路段）、土地利用单元以及旅行者属性及其相互作用进行建模。在 SONG 中，网络拓扑被视为既定因素，链接和系统属性被建模为替代输入的函数。

SONG 将网络演变建模为自下而上的过程，而不是自上而下的过程。规划者和工程师会争辩说，交通网络投资是现在由中央组织（例如州交通部或都市规划组织）驱动的或协调的决策，这些组织使用预测模型和规划流程来测试和评估替代方案，从而做出重大投资决策。地方管辖区（在一些都市区有很多）对较低级别的道路进行投资。当然，这些组织确实会影响新的投资，但建设或扩展链接的决定也受到许多实际情况的制约，例如链接上的实际交通量、竞争的平行链接以及互补的、上游和下游链接、扩展成本以及有限的预算。如果我们能够在没有任何集中规划或指导的情况下生成对网络结构令人信服的表示，那么规划在塑造城市区域方面可能并不像人们有时认为的那样重要，而是相对简单地遵循需求。

这里的示例使用网格网络结构出于以下几个原因。首先，展示的示例测试了替代土地利用模式；同时改变网络拓扑和土地利用会使关于影响的结论变得更加困难。其次，网格是一种广泛使用的拓扑，可以在美国的大多数地方找到（尤其是中西部和西部，因为 1785 年的土地法令建立了公共土地测量系统），网格的基本结构是在确定更详细的因素（如街道宽度（以及它们的重要性））之前就已经确定的。以及相关的土地利用。第三，网格不仅限于美国，它已在各种地方以各种形式使用，其中包括埃及的吉萨、印度河流域的摩亨佐·达罗、汉谟拉比时代的巴比伦、中国和其他亚洲国家的各种首都城市、由希波达摩斯设计的希腊城市（如米利都）、大多数罗马城市规划、墨西哥的特奥蒂瓦坎以及整个美洲的西班牙殖民地。当然，也可以测试其他网络拓扑（或拓扑的缺失），留给学生作为练习。

土地利用和出行产生

土地利用被建模为称为土地利用单元的土地块的网格排列。每个土地利用单元存储其位置、人口密度和市场密度（零售和办公空间的聚合）。使用这些数据，出行产生模型计算从每个土地利用单元吸引和产生的出行。为了简化分析，假设从土地利用单元产生的出行与人口密度成正比，而吸引到土地利用单元的出行与市场密度成正比。因此，土地利用单元所持有的信息可以被视为产生的出行。

令 $(x',y')$ 为表示土地利用单元位置的有序对，其中 $x'$ 是单元在 x 方向上的位置， $y'$ 是单元在 y 方向上的位置。令 $X$ 和 $Y$ 分别表示在 $x$ 和 $y$ 方向上的土地利用单元总数。令 $p(x',y')$ 和 $q(x',y')$ 分别是土地利用单元 $(x',y')$ 产生的出行和吸引的出行。由于地理区域中产生的出行总数等于吸引的出行总数，因此以下等式始终成立。

$\sum \limits _{({x}',{y}')}^{(X,Y)}{p({x}',{y}')=\sum \limits _{({x}',{y}')}^{(X,Y)}{q({x}',{y}')}}$

每个土地利用单元被分配到最近的网络节点。土地利用单元与其最近网络节点之间的通勤成本被忽略。通过将分配到该网络节点的所有土地利用单元的出行量加起来，计算网络节点产生的总出行量和吸引的总出行量。令 ${O_{n}}$ 表示所有距离网络节点 $n$ 比其他任何网络节点更近的土地利用单元集合。通过比较土地利用单元与其周围网络节点之间的距离，将最近的网络节点分配给土地利用单元。每个网络节点的出行量就是分配给它的所有单元的出行量的总和。

$p_{r}=\sum \limits _{\forall ({x}',{y}')\in \{O_{r}\}}{p({x}',{y}')}$

$q_{s}=\sum \limits _{\forall ({x}',{y}')\in \{O_{s}\}}{q({x}',{y}')}$

其中，

$p_{r}$ 是从网络节点 $r$ 产生的（发起的）出行量，

$q_{s}$ 是吸引到（目的地为）网络节点 $s$ 的出行量。

网络层

任何网络都可以被视为由连接在一起的节点（或顶点）和链接（或边或弧）组成的集合。此处的交通网络是有向图 ${G}$ 。令 ${N}$ 表示按顺序编号的节点，并令 ${A}$ 表示按顺序编号的有向链接，连接 ${N}$ 中的节点。令 $N$ 表示集合 ${N}$ 中的元素数量（节点数量），而 $A$ 表示集合 ${A}$ 中的元素数量（链接（或弧）数量）。令 ${R}$ 表示一组起点节点，而 ${S}$ 表示一组终点节点。请注意，在本文建模的网络中， ${R}={S}={N}$ ，即每个节点都充当起点和终点。从起点节点 $r$ 连接到终点节点 $s$ 的链接 $a$ 表示为 $r\rightarrow s$ 。

令 $x_{n}$ 和 $y_{n}$ 表示节点 $n\in {N}$ 在笛卡尔坐标系中的 $x$ 和 $y$ 坐标。令 $l_{a}$ 为边 $a$ 的长度。那么 $x_{n}$ 和 $y_{n}$ 是节点 $n$ 的静态变量，而 $l_{a}$ 是边 $a$ 的静态属性。令 $v_{at}$ 为时间步长 $t$ 时，边 $a\in {A}$ 上车辆的平均速度，称为边速度。边上的行驶时间，即边长与边速度之比，是流量的阻抗。假设网络节点没有流量阻抗。由于图中的边是有方向的——例如，从节点 1 到节点 2 的边不同于从节点 2 到节点 1 的边——因此我们得到一个有向图。

出行分配模型

出行分配将从一个起点产生的出行分配到一个目的地，形成一个起点-目的地矩阵（OD 矩阵），其中行表示每个区域的出行起点总数，列表示每个区域的出行目的地总数。

令 $m_{rst}$ 为时间步长 $t$ 时，从网络节点 $r$ 出发，到达网络节点 $s$ 的出行数量。那么，以下关系在每个时间步长 $t$ 都成立。

$p_{r}=\sum \limits _{s=1}^{N}{m_{rst}^{}}\forall r\in \{N\}$

$q_{s}=\sum \limits _{r=1}^{N}{m_{rst}^{}}\forall s\in \{N\}$

本研究采用单约束重力模型 (Hutchinson, 1974)。每个 OD 对的出行量为

$m_{rst}^{}=p_{r}{\frac {q_{s}\cdot h(d_{rst}^{})}{\sum \limits _{s}{q_{s}\cdot h(d_{rst}^{})}}}\forall r,s\in \{N\}$

其中，采用负指数模型

$h(d_{rs})=e^{-w\cdot d_{rs}}$

使得

$d_{rst}^{}=\sum \limits _{a\in A}{d_{at}^{}}\delta _{a,rst}^{}\forall r,s\in \{N\}$

其中： $\delta _{a,rst}$ 是虚拟变量，如果链接 $a$ 属于 $r$ 和 $s$ 之间的最短路径，则为 1，否则为 0。

$d_{at}$ 是在弧 $a$ 上出行的广义成本。

$d_{rst}$ 是在节点 $r$ 和 $s$ 之间出行的广义成本。

为了定义任何两个节点之间出行的广义成本，有必要定义在链接上出行的广义成本。在时间步长 $t$ 上，在链接 $a$ 上出行的广义成本假设由两部分组成：转换为货币价值的出行时间和通行费，通行费允许根据链接长度和速度变化。

$d_{at}^{}={\frac {l_{a}}{v_{at}^{}}}+\rho _{0}(l_{a})^{\rho _{1}}(v_{a}^{t})^{\rho _{3}}$

其中

$d_{a}t$ 是弧 $a$ 上的通勤泛化成本

$\rho _{0}$ 是基本通行费（使用单位长度和速度的连接的固定成本）

$\rho _{1}$ 是一个系数，代表连接长度的定价结构：通行费相对于长度的弹性

$\rho _{3}$ 是一个系数，代表连接速度的定价结构：通行费相对于速度的弹性

路线分配

使用 OD 矩阵和使用 Dijkstra 算法（Chachra 等人，1979）计算的最短路径信息，可以通过将经过该连接的任何起点和终点的行程进行求和来计算每个连接上的流量。

$f_{at}^{}=\sum \limits _{rs}{m_{rst}^{}\delta _{a,rst}^{}\forall a\in A}$

其中， $f_{at}$ 是时间步长 $t$ 中连接 $a$ 上的交通流量。

收益模型

收益模型估计收取的收益，其中收益仅仅是通行费和流量的乘积。通行费本身是一个泛化函数，如上式 $d_{at}$ 中所述，它随长度和速度而变化。收益 ( $E_{at}$ ) 是第 $t$ 年每个连接可用的资金。

$E_{at}^{}=(\rho _{0}\cdot (l_{a})^{\rho _{1}}(v_{a}^{t})^{\rho _{3}})\cdot (\psi \cdot f_{at}^{})\forall a\in A$

其中： $\psi$ 是将流量年化的模型参数。

成本模型

在经验模型中，通常发现高速公路维护和扩建的成本可以用科布-道格拉斯形式很好地表示（例如 Levinson 和 Gillen 1998 以及 Levinson 和 Yerra 2002，他们都发现科布-道格拉斯模型比其他函数形式更适合）。成本通常是产出（例如，按车辆类型划分的流量）、网络规模、价格和质量指标的函数。该模型不考虑价格（假设价格是外生的，并且随着时间的推移是固定的（或以与收入相同的速率上升）），但考虑了其他三个变量。维护链接 $(C_{at})$ 在某一年中的成本由下式给出：

$C_{at}^{}=\mu \cdot (l_{a})^{\alpha _{1}}(f_{at}^{})^{\alpha _{2}}(v_{at}^{})^{\alpha _{3}}f_{at}^{}\forall a\in A$

其中

$\mu$ 是（年度）链接维护的单位成本。

$\alpha _{1},\alpha _{2},\alpha _{3}$ 是表示关于长度、流量、速度的规模经济或规模不经济的系数。

投资模型

在提出的投资模型中，如果一个链接代理人在某一年中存在超额收益（超出维持链接当前速度所需的收益），它可以使用该收益来改善链接（使其更快）。如果一个链接出现赤字，它就无法负担全部维护费用，链接速度就会下降。反映这一点的方程由下式给出：

$v_{at+1}^{}=v_{at}^{}\left({\frac {E_{at}^{}}{C_{at}^{}}}\right)\forall a\in A$

在文献中，迄今为止还没有经验投资模型可供参考，因此该函数具有一定的随意性。必须承认，投资模型很简单且短视，我们认为，如果它能够再现被认为是由更复杂过程产生的结果，那么这将是该模型的优势。未来的研究可以测试替代的投资模型，包括使用政府或银行等中央代理人来重新分配超额资金的投资，或者即使链接无利可图，也要确保提供基本的服务水平。

应用平均规则以确保链接及其反向链接共享相同的设计，这是道路的典型特征。

$v_{at+1}^{}=v_{{a}'t+1}^{}={\frac {v_{at+1}^{}+v_{{a}'t+1}^{}}{2}}$

如果从交通分配模型中应用对称条件，则不需要应用此条件，因为这些对称条件会自动确保 $a$ 和 $a'$ 具有相同的流量。

实验

考虑了三种土地利用模式：随机、均匀和钟形。以下各小节将详细介绍每个类别。

随机分布的土地利用

土地使用属性（如人口和就业）的空间分布取决于许多因素，其中一些变量是相互依存的。在随机分布的土地使用中，每个土地使用单元格产生的出行量和吸引的出行量在整个地理区域内都是随机分布的。产生的和吸引的出行量分布在给定的最小值和最大值之间。

$p({x}',{y}'),q({x}',{y}'){\tilde {\ }}Un(u_{\min },u_{\max })$

统一土地使用

可以通过使用方程式 (14) 中所示的分布来分配统一的土地使用模式，其中每个单元格在整个地理区域中都具有相同的属性，使用相同的 $u_{min}$ 和 $u_{max}$ 值。这种土地使用模式是控制土地使用对道路等级形成影响所必需的。

钟形土地使用

实际上，土地使用的分布并不完全随机。在具有中央商务区的城市地区，土地使用变量的分布通常可以表示为钟形或倒钟形的曲面。在这种情况下，吸引的出行量 $q(x',y')$ 被建模为沿半径接近地理区域中心时增加。产生的出行量与住宅密度成正比，假设在中心处最小，类似于倒钟形的曲面。图 2 显示了沿半径方向假设的产生的出行量和吸引的出行量分布的横截面的示意图。吸引的出行量空间分布函数如方程式所示

$q({x}',{y}')=u_{\min }+(u_{\max }-u_{\min })e^{-z^{2}(({x}'-d_{x})^{2}+({y}'-d_{y})^{2})}$

其中， $d_{x})$ 是市中心沿 x 轴土地使用单元格的位置，

$d_{y}$ 是市中心沿 y 轴土地使用单元格的位置， $z)$ 是一个取决于市中心范围的因素。

将上述方程式中的 $q(x',y')$ 代入初始方程式，得到

$\sum \limits _{({x}',{y}')}^{(X,Y)}{p({x}',{y}')}=\sum \limits _{({x}',{y}')}^{(X,Y)}{q({x}',{y}')}=X\cdot Y\cdot u_{\min }+(u_{\max }-u_{\min })\sum \limits _{({x}',{y}')}^{(X,Y)}{e^{-z^{2}(({x}'-d_{x})^{2}+({y}'-d_{y})^{2})}}$

假设出行产生的表面呈倒置钟形，则 $p(x',y')$ 的分布是使用以下公式计算的

$p({x}',{y}')=u^{*}-(u_{\max }-u_{\min })e^{-z^{2}(({x}'-d_{x})^{2}+({y}'-d_{y})^{2})}$

其中，

$u^{*}=u_{\min }+{\frac {2(u_{\max }-u_{\min })}{X\cdot Y}}\sum \limits _{({x}',{y}')}^{(X,Y)}{e^{-z^{2}(({x}'-d_{x})^{2}+({y}'-d_{y})^{2})}}$

模型参数

表 1 给出了模型中参数的值。这些参数在注明的情况下已被固定，以便在本次研究中对感兴趣的变量（土地利用模式）进行可比性分析。初始速度被赋予单位值，土地利用（每个单元格产生的和吸引的出行次数）在基本情景中为 10 个单位。土地利用实验中的出行分配模型系数 ( $w$ ) 为 0.01，除非另有说明；较高的系数意味着旅行者对旅行成本更加敏感，因此会进行更短的旅行，这些情况将在单独的测试中进行测试。通行费设置为与路线长度线性增长，并且不受道路质量（速度）的影响。收入和成本系数被缩放以假设 365 天中的每一天都是相等的，以使价值年化（这显然是一种理想化，忽略了例如周末）。成本随长度线性增长。然而，存在规模经济，因此流量增长 1%，成本仅增长 0.75%。同样，当速度增长 1% 时，成本仅增长 0.75%。这种规模经济的一般假设得到了文献的支持，尽管确切的幅度存在争议。Small、Winston 和 Evans（1989）报告了与路面厚度相关的显著规模经济，这体现了其承载负荷的能力。他们还发现，在提供道路容量方面存在轻微的规模经济；即承载交通的能力。Yerra 和 Levinson（2002）也报告了汽车和卡车的规模经济。为了能够探索感兴趣的变量，这些参数再次被固定。

变量	描述	'	基本假设

$v_{a0}$	初始速度（整数）	1
$g_{z},h_{z}$	网格 z 的土地利用属性	10
$w$	出行分配模型中的系数（土地利用实验）	0.01
$\rho _{0}$	收益模型中的系数	1.0
$\rho _{1}$	收益模型中的长度幂	1.0
$\rho _{3}$	收益模型中的速度幂	0.0
$\tau$	收益模型中的税率	1.0
$\psi$	收益模型参数	365
$\mu$ μ	成本模型中的单位成本	365
$\alpha _{1}$	成本模型中的长度幂	1.0
$\alpha _{2}$	成本模型中的流量幂	0.75
$\alpha _{3}$	成本模型中的速度幂	0.75

结果

土地利用实验

基本案例：初始速度和土地利用均匀分布 (U/U) - 初始网络中均匀速度的空间分布
基本案例：初始速度和土地利用均匀分布 (U/U) - 网络在经过 8 次迭代后达到平衡时的速度空间分布。
初始速度均匀分布，初始土地利用随机分布 (U/R) - 实验 U/R 达到平衡后的速度空间分布
初始速度随机分布，初始土地利用随机分布 (R/R) - 实验 R/R 的初始速度空间分布（初始速度随机分布，初始土地利用随机分布）
初始速度随机分布，初始土地利用随机分布 (R/R) - 网络达到平衡后的速度空间分布；连线的颜色和粗细表示其相对速度或流量。
初始速度均匀分布，初始土地利用呈钟形分布 (U/B) - 实验 U/B 的最终速度空间分布（初始速度均匀分布，土地利用呈钟形分布）

土地利用结果显示在图 3-7 中。图 3 展示了基本案例，初始网络和初始土地利用均匀分布（表示为 (U/U)）。在基本案例中，一个没有差异的网络演化成为一个高度差异化的网络，既包含一条主要的南北轴和东西轴，也包含两条环形道路。其他图与基本案例相似，都具有层次结构，但有所不同，因为层次结构没有那么规则或对称。这些案例与基本案例的初始状态相同，但初始速度和土地利用特性的处理方式不同。在土地利用随机分布的实验中，网格的土地利用特性在 10 到 15 次出行之间随机分布。在这种情况下，从土地利用网格产生的出行和吸引到该网格的出行不必相同，尽管所有土地利用网格产生的出行总数和吸引的出行总数相同。本模型中的连线速度采用两种处理方式；首先（实验 U/R），假设每条连线的速度都相同，大小为 1，与基本案例相同。其次（实验 R/R），速度在 1 到 5 之间随机分布。典型的解决方案如图 4 和 5 所示。

请注意实验 U/R 和 R/R 的结果网络的相似性。我们认为土地利用分布（和速度）以及边界是造成这种层次结构的原因。

图 6 (U/B) 和 7 (R/B) 采用了城市钟形土地利用分布。城市土地利用分布使得网络中心与杯形吸引的出行和产生的出行函数的中心重合。由于更多出行被吸引到网络中心，因此自然会期望通往中心的连线承载较高的交通量。请注意图 6 中 X 和 Y 方向主要道路的均匀间距，以及主要道路都通向网络中心，那里集中了大部分活动。图 6 中中心周围有三个环，而图 3 中只有两个主要环。此外，主要的南北轴和东西轴发生分叉，部分交通量被引流到环形道路，而其他交通量则继续通过中心。图 7 的初始速度随机分布，其模式与图 4 或 5 相似，中心周围只有一个不对称环，尽管它被偏移，因为随机的初始条件会导致不同的结果网络。空间互动实验

空间互动参数实验

重力模型参数变化，网络和土地利用均匀分布 (U/U) $w=0.02$ (对出行成本不太敏感) 时，平衡状态下相对速度的空间分布。
重力模型参数变化，网络和土地利用均匀分布 (U/U) $w=0.8$ (对出行成本更敏感) 时，平衡状态下相对速度的空间分布。
对于 10X10、11X11 和 15X15 网络，平均连接速度随 w 的变化。

在另一个实验中，摩擦系数中的系数 ( $w$ ) 表示出行行为，测试了其敏感性并比较了结果。在这些实验中，网络和土地利用都与基本假设一致，因此这是 (U/U) 的一个变体。如果 w 为零，则出行分配与出行成本无关。w 的较高 (较低) 值代表一个社会，其中较短 (较长) 的出行更频繁。图 8 比较了代表更喜欢短途旅行和长途旅行的两个 w 值的平衡空间速度分布。正如预期的那样，较大 $w$ 的速度空间分布更平坦，具有更多相对高速的连接，而更喜欢长途旅行的社区则更加分层。然而需要注意的是，虽然更喜欢短途旅行的社区拥有更多相对高速的连接，但它们的绝对高速连接并不更多，也就是说，它们的平均连接速度低于更喜欢长途旅行的社区。

图 9 和 10 显示了几个网络大小下平均交通流量和速度相对于系数 w 的变化。正如预期的那样，随着 w 的增加，网络上的平均交通流量 (速度) 下降，表明出行距离更长的社会产生更多交通收入，因此会产生更好的交通基础设施。

结论

本分析测试了三种不同类型的土地利用 (随机、均匀和钟形) 对网格网络的影响。每种土地利用都会产生不同的道路等级结果，一些会产生更显著的环形道路，另一些则会产生更平坦的网络模式。一个改变出行分配 (空间互动) 模型中摩擦系数的实验表明，该参数对道路的空间分布影响很大。我们可能会观察到，在拥堵 (系统的外部性) 成为问题或存在对脆弱连接可靠性的担忧的情况下，有时拥有更平坦的连接流量等级分布是有利的。所有这些情景都让我们得出结论：道路等级是交通网络与使用者相互作用的涌现属性。这一发现是在非常简单的收入、成本和投资假设下发生的。道路的涌现表明网络能够自组织。

自组织网络可以规划吗？规划的难度在于，由于缺乏合适的预测工具，交通网络的长期形态动态一直以来在本质上是不可预测的，并且它们依赖于许多外生的社会、经济、政治和技术变化。我们观察到，在许多方面，城市都是自组织的，而关于分形城市 (Batty and Longley 1994) 的最新文献也支持这一点。与“市场”均衡不同的个人投资决策将塑造市场或网络的未来发展。显然，城市既是自组织的，也是规划的。网络也可以做到。本文开发的模型使我们能够模拟规划决策和决策规则对网络未来形态的影响。当与土地利用模型相结合时，可以生成城市系统的完整模型，使我们能够更全面地了解导致城市问题（如拥堵和蔓延）的因素。这些工具使我们能够在模型中探索这些问题以及可能的解决方案，从长远来看，这应该比在运作的城市进行现实世界实验更具成本效益，而现实世界实验通常是不可行的。人们认为，根据类似于本研究中提出的复杂系统原理建模的基于代理的网络动态可能会被证明是有用的。

例如，在现实中，土地利用分布既不是均匀的，也不是完美的钟形曲面。它是一个非常崎岖的地形，具有不连续性，只有某些小区域显示出趋势。这里介绍的方法提供了使用现实土地利用模式 (例如 Zhang and Levinson 2004) 的灵活性，这提供了更多证据来证明模型框架的效用，但缺点是具有多个同时存在的方面，这些方面不像人工网络和土地利用模式那样容易解开。

面对自组织网络，需要某种机制来消除负面外部性。对旅行者的干预点众所周知（例如，对出行进行适当的定价），但对建造网络的代理的干预迄今为止一直留给了政治。这些代理使用了一些规则（这里高度简化），这些规则导致机构扩展连接，这些规则通常是根据有限的标准制定的（例如，当平均日交通量超过 X 且路面状况不佳时扩展）。更好地理解这些规则以及它们如何在一个系统动态框架中随着时间的推移发挥作用，为我们提供了一种减少与交通相关的负面影响的另一种方式。

如前所述，土地利用与交通网络动态之间的关系至关重要。许多当前的城市问题都是由于拥堵和蔓延造成的，而这些问题是土地利用与出行需求和交通基础设施供应之间的不平衡的副产品（或解决方案）。虽然本文提出的模型没有明确考虑网络对土地利用的影响，但人们推测，对这种反馈关系进行建模将有助于规划交通项目，为管理拥堵和蔓延提供必要的基础设施。此外，此类模型可以成为城市和交通规划者的有效工具。大多数传统的交通规划模型将土地利用视为一个给定的变量（如本模型中），但通过包含土地利用的动态，可以捕捉到更丰富的交通以及城市动态。

参考文献

Barabasi A, Albert R 1999 “Emergence of scaling in random networks.” Science 286 509-512
Barabasi A, Albert R, Jeong H 1999 “Scale-free characteristics of random networks: the topology of the world wide web” Physica A 272 173-187
Batty M, Longley P 1994 Fractal Cities (Academic Press, London)
Chachra V, Ghare P, and Moore J 1979 Applications of Graph Theory Algorithms. (North Holland, New York)
Christaller W 1933 Central Places in Southern Germany (Fischer, Jena, Germany) (English translation by Baskin, C (Prentice Hall, London 1966)).
Fujita M, Krugman P, Venables, A 1999. The Spatial Economy: Cities, Regions, and International Trade (MIT Press, Cambridge, MA)
Garrison W, Marble, D 1965 A Prolegomenon to the Forecasting of Transportation Development. United States Army Aviation Material Labs Technical Report (Office of Technical Services, United States Department of Commerce, Washington, DC)
Helbing D, Keltsch J, Molnár P 1997 “Modeling the evolution of human trail systems” Nature 388: 47.
Hutchinson B 1974 Principles of Urban Transportation Systems Planning. (McGraw-Hill, New York)
Lam L, Pochy R 1993 “Active-walker models: growth and form in non-equilibrium systems” Computation simulation 7, 534.
Lam L 1995 “Active walker models for complex systems” Chaos, Solitons and Fractals 6, 267-285.
Levinson, D and Gillen, D 1998, “The Full Cost of Intericty Highway Transportation” Transportation Research part D 3:4 207-223,
Levinson D and Karamalaputi R 2003a “Predicting the construction of new highway links” Journal of Transportation and Statistics 6(2/3) 81–89
Levinson D and Karamalaputi R 2003b, “Induced supply: a model of highway network expansion at the microscopic level” Journal of Transport Economics and Policy, 37(3) 297–318
Levinson, D and Yerra, B. 2002 “Highway Costs and the Efficient Mix of State and Local Funds” Transportation Research Record: Journal of the Transportation Research Board 1812 27-36
Levinson D 和 Yerra B 2005 “地面交通网络的自组织” 交通科学 (即将出版)
Lösch A 1954 地点经济学 (耶鲁大学出版社，纽黑文)
Schweitzer F，Schimansky-Geier L 1994 “双组分系统中活跃步行者的聚类” 物理学 A 206 359-379
Small, K, Winston, C & Evans, C 1989 公路工程：一项新的高速公路投资政策。华盛顿特区：布鲁金斯学会。
Taaffe E，Morrill R，Gould P 1963 “发展中国家的交通扩展：比较分析。” 地理评论 53 (4) 503-529
Watts D，Strogatz S 1998 “‘小世界’网络的集体动力学”，自然 393: 440-442。
Yamins D，Rasmussen S，Fogel，D 2003 “城市道路的增长” 网络与空间经济学 3 69-85
Yerra B，Levinson D 2004 “交通网络中层次结构的出现” 地区科学年鉴 (即将出版)。
Xie, F., Levinson D 2011 演进中的交通网络，施普林格。
Zhang L，Levinson D 2004 “道路兴衰模型” 2004 年 3 月麻省理工学院工程系统研讨会论文，剑桥，马萨诸塞州；可从 Levinson，明尼苏达大学土木工程系，明尼阿波利斯获得副本