使用 SPSS 和 PASW/普通最小二乘回归

普通最小二乘 (OLS) 回归（或简称“回归”）是用于检查两个或多个区间/比率变量之间关系的有用工具。OLS 回归假设两个变量之间存在线性关系。如果关系不是线性的，则 OLS 回归可能不是分析的理想工具，或者可能需要对变量/分析进行修改。线性回归的基本思想是，如果两个变量之间存在线性关系，则可以使用一个变量来预测另一个变量的值。例如，由于身高和体重之间存在线性关系，如果您知道某人的身高，就可以更好地估计他们的体重。使用基本线公式，您可以使用自变量计算因变量的预测值，从而做出更好的预测。

为了说明如何在 SPSS 中进行回归分析，我们将使用样本数据集中的两个区间变量。这些相同的变量在其他一些章节中使用过。遗传咨询师被要求根据 10 分制对他们认为自己的宗教和精神程度进行评分 - 较高的值表示更宗教或更精神。在下面的分析中，我们将看看宗教程度如何预测精神程度。

在我们计算遗传咨询师的宗教程度和精神程度的回归线之前，我们应该做的第一件事是检查这两个变量的散点图。散点图将帮助我们确定两个变量之间的关系是线性的还是非线性的，这是回归分析的一个关键假设。这在 SPSS 中通过转到“图形” -> “图表构建器”来完成。

选择“图表构建器”后，您将获得“图表构建器”窗口，它看起来像这样

在“图表构建器”窗口中，在屏幕中间确保您选择了“库”选项卡，然后从选项列表中选择“散点图”。在选项的右侧，您将看到 8 个框。如果您将鼠标悬停在这些框上，它们将识别它们将生成的散点图类型。选择左上角的选择，称为“简单散点图”。要选择它，您需要将其拖动到上面写着“图表预览使用示例数据”的框中。然后您将看到两个轴 - Y 轴和 X 轴。在我们的示例中，由于我们使用宗教程度来预测精神程度，因此我们将 relscale 拖动到 X 轴，将 sprscale 拖动到 Y 轴。然后我们选择“确定”，并在我们的输出窗口中获得以下内容

具有大量值的散点图通常很难解释。SPSS 试图通过使具有大量出现的点更暗来使解释变得更容易。在这种情况下，我们在散点图中可以看到，似乎有一条深色的线从左下角跑到右上角，表明宗教程度和精神程度之间存在正相关关系 - 一个增加，另一个也增加。该关系也似乎是线性的，这对于回归分析来说是件好事。在检查了散点图后，我们现在可以进行回归分析。

要在 SPSS 中运行回归分析，请选择“分析” -> “回归” -> “线性”。

将打开“线性回归”窗口。

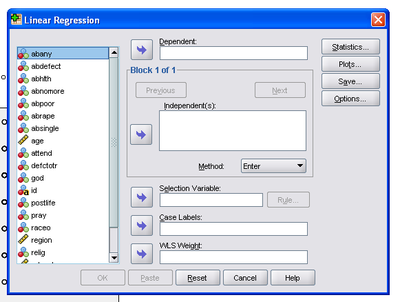
左侧是变量列表。找到您的因变量。在我们的示例中，它是“sprscale”。我们使用箭头将其移动到“因变量”框中。然后找到您的自变量。在我们的示例中，它是“relscale”。我们将其移动到“自变量：”框中。

虽然可以选择许多其他选项，但基本选项足以用于示例。因此，选择“确定”，您将在输出窗口中获得以下内容

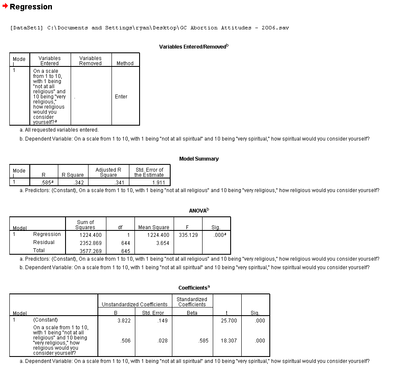
第一个表格只是告诉您哪些变量包含在分析中以及它们是如何包含的（即，哪个是自变量，哪个是因变量）。

第二个表格提供了“模型摘要”，我们稍后将回到它。第三个表格是方差分析表，它对于各种统计数据非常有用，但我们将在本章中暂时跳过它。

第四个表格提供了对我们当前努力最有意义的回归统计数据。第二行（不是标记为“(常数)”的第一行）的第一列“B”提供了自变量的斜率系数。这意味着，对于自变量的每个 1 个单位变化，因变量将发生 XX 个单位变化。在我们的示例中，10 分制宗教程度量表的每 1 分增加，会导致精神程度量表增加 0.506 分。这告诉我们我们在散点图中注意到的两个变量之间的关系是准确的 - 关系是正的。

第二列，标记为“标准误差”，提供了斜率系数的标准误差。第三列“Beta”提供了斜率系数的标准化版本（在二元回归中，这也被称为相关系数或“r”）。这意味着，对于自变量的每个 1 个标准差单位变化，因变量将发生相应的 XX 个标准差单位变化。对于大多数变量来说，这不如斜率系数直观。第四列“t”是 t 统计量。第五列“Sig.”提供了自变量斜率系数的 p 值。在我们的示例中，p 值为 0.000，小于标准 alpha 值 0.05，表明在假设实际上不存在关系的情况下，偶然发现我们所做的宗教程度和精神程度之间的线性关系的可能性小于千分之一。换句话说，我们可以拒绝宗教程度和精神程度之间不存在关系的零假设，并接受宗教程度和精神程度之间存在显著关系的备择假设。从实际意义上讲，更宗教的遗传咨询师往往也更精神。

第四个表格的第一行提供了常数或 y 截距的统计数据。在本章中，我们最感兴趣的是“B”列中的值。该值是 y 截距，或回归线与 y 轴相交的点。在我们的示例中，它是 3.822。这意味着，当遗传咨询师的宗教程度为零时，精神程度预测为 3.822。

回到第二个表格，敏锐的读者会注意到第一列“R”与第四个表格中的“Beta”列相同。如上所述，二元回归中的标准化斜率系数等同于相关系数或“r”。第二列是 R 平方统计量，它是由统计模型解释的数据集中可变性的比例。基本上，R 平方统计量可以解释为：宗教程度解释了精神程度变化的 34.2%。

最后，为了说明回归线作为我们数据集中许多案例的最佳拟合线的实际线，我们添加了另一个带回归线的散点图。

此图说明了回归线试图最小化散点图中所有点之间的变化，为自变量（宗教程度）的每个值提供因变量（精神程度）的最佳估计。它还显示了回归线在上面提到的值（3.822）处与 y 轴相交。

以上解释应为个人提供足够的信息来运行回归分析并在 SPSS 中解释它。