维基少年:儿童编程/设计你的解决方案

一旦我们弄清楚了我们的问题，我们就需要设计一个解决问题的方法。在这个阶段，我们还没有编写任何代码。我们只是在制定一个框架，我们将在算法设计阶段遵循这个框架。

分治法

分治法 (D&C) 来自拉丁语 divide et impera。它指的是将一个大问题分解成更小的子问题。子问题可以进一步细分为更小的子子问题，然后变成子子子问题，等等，你懂的。分治法是一种系统化的方式，可以为你的解决方案提供一个蓝图。在每个子问题都解决后，我们将它们合并在一起，形成“大局”。

分治法可以应用于现实生活中的问题和编程问题。我们将在下一节中查看一个著名的应用程序，数组排序。现在，让我们尝试一些更简单的事情。假设你想测量一个体育场的面积。没有直接计算体育场大小的公式，所以让我们尝试这样操作

此图是一个结构图。结构图是映射解决方案结构的一种方式。（不意外吧！）

让我们尝试一个更难的问题。假设你有一个方形的花坛和一个围绕它的路径。你需要铺设这条路，并想计算这个项目的总成本。你会怎么做？

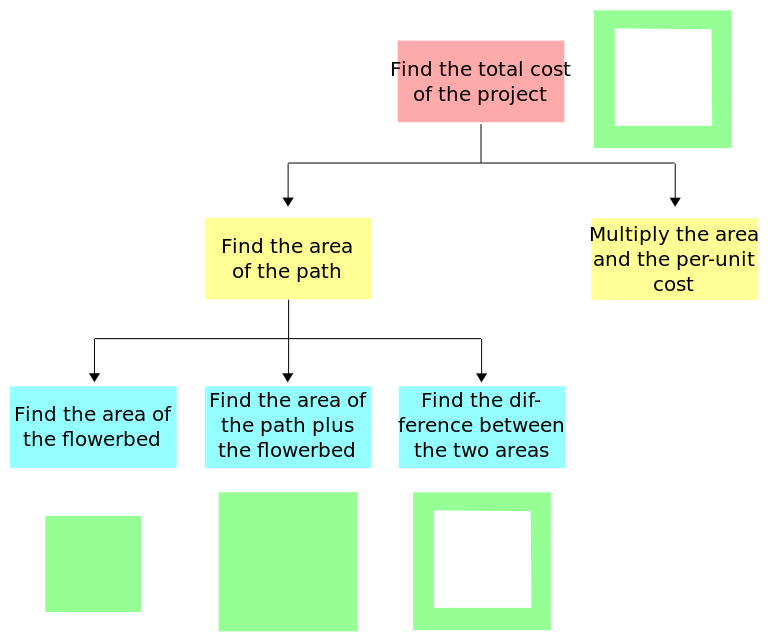
请注意，这个问题涉及将问题分解成更小的子问题。

模块化方法

通过对我们的问题使用 D&C，我们正在采用模块化方法进行编程。在上面的图表中，每个块代表一个模块。在第二个图表中，可以将子子问题称为子模块。将问题分解成不同的模块是一种常见的编程实践。

数据和信息在结构图中以某种方式流动。例如，在花坛示例中，'查找两个区域之间的差异' 模块需要知道 '查找花坛区域' 和 '查找路径加花坛区域' 模块中的数据。为了清晰地表示这一点，每个模块都有一个模块规范，它清楚地记录了模块的输入、输出和过程。我们也可以为此目的使用 I-P-O 图表。让我们看一下花坛项目的模块规范。（如果你没有完全理解所有内容，不要担心；我们很快就会看到它们。）

模块：'查找项目的总成本'
输入	过程	输出
花坛的宽度 花坛的长度 整个区域的宽度 整个区域的长度 每单位成本	提示用户输入花坛的尺寸、整个区域的尺寸和每单位成本 获取花坛的尺寸、每单位成本的尺寸 验证输入数据 查找路径的面积 将面积和每单位路径相乘 将项目的总成本输出到屏幕上	项目的总成本

模块：'查找路径的面积'
输入	过程	输出
花坛的宽度 花坛的长度 整个区域的宽度 整个区域的长度	读取花坛的尺寸、整个区域的尺寸 查找花坛的面积 查找路径面积加上花坛面积 查找两个区域之间的差异 输出路径的面积	花坛的面积

模块：'将面积乘以每单位成本'
输入	过程	输出
路径的面积 每单位成本	读取路径的面积和每单位成本 根据需要转换路径和成本的单位 将路径的面积乘以每单位成本 输出项目成本	项目的总成本

模块：'查找花坛的面积'
输入	过程	输出
花坛的长度 花坛的宽度	读取花坛的尺寸 将路径的长度和宽度相乘 输出花坛的面积	花坛的面积

模块：'查找路径加花坛的面积'
输入	过程	输出
整个区域的长度 花坛的宽度	读取整个区域的尺寸 将路径的长度和宽度相乘 输出整个区域	花坛的面积

模块：'查找两个区域之间的差异'
输入	过程	输出
花坛的面积 整个区域	读取两个区域 查找两个区域之间的差异 输出路径的面积	路径的面积

模块化方法有很多优点。

模块化方法允许我们重用模块。

• 它允许在编程中更加灵活。模块化方法促进了代码重用。有时，一个模块可能在一个程序中被使用多次。例如，在一个几何程序中，希望有一个单一的模块用于勾股定理，它可以在程序中的任何时候使用。这可以节省我们复制粘贴（并且可能会在此过程中出错）的时间。此外，一个模块的更改可能不会对整个程序产生重大影响。

模块化方法鼓励团队合作。

• 一次解决一个小问题更容易。如果我们将程序分成各个模块，更容易看到程序的结构。一大块代码很难阅读和调试。将其分成更小的部分有助于识别和纠正错误。
• 它鼓励程序员之间的协作。一群程序员可以将工作分配到不同模块，并将其分配给每个人。它还促进专业化：例如，一个熟悉 XML DOM 的程序员可以选择从事 XML 方面的工作，而另一个熟悉 SQL 的程序员可以选择从事数据库和 PHP 方面的工作。它还便于管理和控制。

模块化方法也有缺点。例如，每个团队成员可能不清楚整个程序是如何工作的。因此，他们可能不知道全貌。这可能会导致不同模块之间的链接出现问题。它还需要为其他程序员进行大量深入的文档记录，这会增加时间和成本。

等等...

我们已经使用模块化方法设计了程序的框架，但我们应该从哪里开始呢？我们应该先处理最小的程序，然后逐步向上吗？还是应该先处理最上面的部分，然后逐步向下？阅读下一章，找出答案！