A-level 化学/OCR (Salters)/分子几何
外观
分子的形状 是 化学理念 中第 3.3 节的标题,它涵盖了分子几何结构 的主题。
-
点交叉图 -
键线图 -
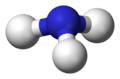
球棍模型
-
点交叉图 -
键线图 -
显示孤对电子的球棍模型 -
不显示孤对电子的球棍模型
-
点交叉图 -
键线图 -
显示孤对电子的球棍模型 -
不显示孤对电子的球棍模型
-
点交叉图 -
键线图 -
显示孤对电子的球棍模型 -
不显示孤对电子的球棍模型
你可能之前在数学中遇到过四面体,尽管你很可能称它们为三角形基金字塔。四面体有四个顶点(角)、四个面和六条边。每个面都是一个等边三角形。
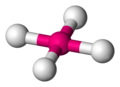
四面体是化学中最重要的形状之一,因为许多分子都包含它们。四面体分子实际上不包含小金字塔。它们包含的是一个中心原子与四个其他原子键合。围绕中心原子的四个原子占据的位置可以想象成四面体的顶点。
在下面的图片库中,中心原子用品红色着色,周围原子用白色着色。
-
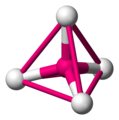
一个四面体分子 -
要看到四面体,用直线连接周围原子 -
这些直线形成了四面体的边 -
四面体角≈ 109.5° -
化学家使用虚线和楔形键来表示四面体 -
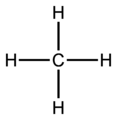
这就是化学家如何表示甲烷 -
这种“扁平”表示 - GCSE 风格 - 更简单,但不太现实
四面体分子中任意两个键之间的角度约为 109.5°。四面体角可以根据需要计算得尽可能精确,因为它等于 cos−1(–⅓)。
你可能之前遇到过或没有遇到过八面体。八面体有六个顶点(角)、八个面和十二条边。每个面都是一个等边三角形。
八面体在化学中非常重要,因为许多过渡金属基分子 是八面体的。
-
一个八面体分子 -
要看到八面体,用直线连接周围原子 -
这些直线形成了八面体的边 -
八面体角 = 90° 正好 -
化学家使用虚线和楔形键来表示八面体 -
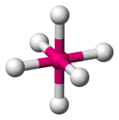
这就是化学家如何表示六氟化硫,SF6 -
SF6 的球棍模型
-
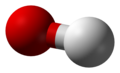
线性的 -
弯曲的 -
三角形的平面 -
锥形的 -
方形平面 -
四面体的 -
三角双锥形的 -
八面体的
你可以使用所谓的AXE 方法来计算分子的形状。它是基于具有中心原子的分子,我们将其标记为 A。与 A 键合的原子或基团标记为 X。孤对电子标记为 E。具有三个孤对电子和两个与之键合的原子/基团的分子将表示为 AX2E3。下表显示了 X 和 E 以及分子形状之间的关系。
价层电子对互斥理论 (VSEPR) 用于在已知 X 和 E 的情况下预测分子的形状。这听起来比实际更复杂。你认为任何 X 和 E 都是电荷区域,它们相互尽可能远离地定位,以最大限度地减少它们之间静电排斥力的作用。
| AXE 标签 | X (取代基) |
E (孤对电子) |
形状 | 2D 图 显示孤对电子 |
2D 图 不显示孤对电子 |
3D 模型 显示孤对电子 |
3D 模型 不显示孤对电子 |
示例 |
|---|---|---|---|---|---|---|---|---|
| AX1E0 | 线性的 | H2 | ||||||
| AX1E1 | 线性的 | CN− | ||||||
| AX1E2 | 线性的 | 
|

|
O2 | ||||
| AX1E3 | 线性的 | 
|

|
HCl | ||||
| AX2E0 | 线性的 | BeCl2 HgCl2 CO2 | ||||||
| AX2E1 | 弯曲的 | 
|

|

|
NO2− SO2 O3 | |||
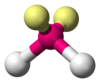
| AX2E2 | 弯曲的 | 
|
|

|
H2O H2S OF2 | |||
| AX2E3 | 线性的 | 
|

|
XeF2 I3− | ||||
| AX3E0 | 三角形的平面 | 
|

|

|

|
BF3 CO32− NO3− SO3 | ||
| AX3E1 | 三角锥形的 | 
|

|

|

|
NH3 PCl3 | ||
| AX3E2 | T 形 | 
|

|

|

|
ClF3 BrF3 | ||
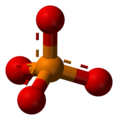
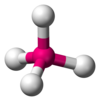
| AX4E0 | 四面体的 | 
|

|
|

|
CH4 NH4+ PO43− SO42− ClO4− | ||
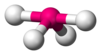
| AX4E1 | 跷跷板形 | 
|

|

|
|
SF4 | ||
| AX4E2 | 方形平面 | 
|

|

|
XeF4 | |||
| AX5E0 | 三角双锥形的 | 
|

|

|

|
PCl5 | ||
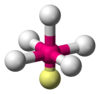
| AX5E1 | 方形锥形的 | 
|

|
|

|
ClF5 BrF5 | ||
| AX5E2 | 五角形的平面 | 
|

|

|
XeF5- | |||
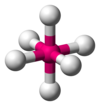
| AX6E0 | 八面体的 | 
|

|
|

|
SF6 | ||
| AX6E1 | 五角锥形 | 
|

|

|

|
IF6- | ||
| AX7E0 | 五角双锥形 | 
|

|

|

|
IF7 | ||
| AX8E0 | 正方反棱柱形 | 
|

|
IF8- | ||||
| AX8E1 | 扭曲的正方反棱柱形 | 
|
XeF82- | |||||
| AX9E0 | 三帽三角柱形 或 顶盖正方反棱柱形 | 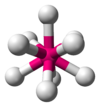
|

|
ReH92- (三帽三角柱形) |