A-level 数学/CIE/纯数学 1/二次方程

配方

配方动画演示

配方是一种将 $ax^{2}+bx+c$ 形式的表达式转换为 $a(x-h)^{2}+k$ 形式的表达式的方法。

它依赖于以下事实：$(x+p)^{2}=x^{2}+2px+p^{2}$.

首先，我们取表达式 $ax^{2}+bx+c$ 并将 $a$ 提取出来得到 $a(x^{2}+(b/a)x+(c/a))$.

然后，我们需要认识到 $(x+(b/2a))^{2}=x^{2}+(b/a)x+(b^{2}/4a^{2})$

示例

假设我们需要将 $x^{2}+4x+3$ 转换为配方形式。

这里，$a$ 为 1，因此我们无需做任何操作来提取它。

接下来，我们认识到 $(x+2)^{2}=x^{2}+4x+4$，需要在表达式中找到它。

$x^{2}+4x+3=x^{2}+4x+4-1=(x+2)^{2}-1$

因此，我们得到了答案：$x^{2}+4x+3=(x+2)^{2}-1$

判别式

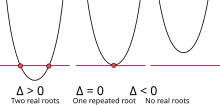判别式告诉您二次函数与 x 轴相交或相切的次数。

判别式 是一个值，我们可以用它来确定二次函数有多少个实根。一个实根 是二次表达式的值为零的地方。

表达式 $ax^{2}+bx+c$ 的判别式计算为 $\Delta =b^{2}-4ac$。

如果判别式大于零，则有两个独立的实根。

如果判别式等于零，则有一个重复根。

如果判别式小于零，则没有实根。

求解二次方程

求解二次方程或不等式主要有三种方法：因式分解、配方法和使用二次公式。

因式分解

因式分解的一个例子

因式分解 是我们将表达式分解为其因子的过程。

例如，$x^{2}+5x+6$ 可以因式分解为 $(x+2)(x+3)$

因式分解可以用来求解方程：如果两个因子的乘积等于零，这意味着其中一个因子必须等于零。

例如，求解 $x^{2}+x-6=0$

${\begin{aligned}x^{2}+x-6=(x+3)(x-2)=0\\\therefore x+3=0\quad or\quad x-2=0\\x=-3\ or\ 2\end{aligned}}$

要分解系数与 $x^{2}$ 项相乘的表达式的因式，只需将系数除掉即可

例如，求解 $3x^{2}+12x+9=0$

${\begin{aligned}3x^{2}+12x+9=0\\x^{2}+4x+3=0&\quad (\div 3)\\(x+3)(x+1)=0\\x=\{-3,-1\}&\quad \leftarrow {\text{Set notation can be used to represent multiple solutions}}\end{aligned}}$

然而，并非所有表达式都能因式分解。

配方

**配方**是指将二次方程从 $ax^{2}+bx+c$ 的形式转换为 $a(x-h)^{2}+k$ 的形式。这使得求解方程变得更容易，并且在所有情况下都能起作用，不像因式分解那样。

例如：求解 $x^{2}+12x-9=0$

${\begin{aligned}x^{2}+12x-9=0\\(x+6)^{2}=x^{2}+12x+36\\(x+6)^{2}-36-9=0\\(x+6)^{2}=45\\x+6={\sqrt {45}}\\x=-6\pm 3{\sqrt {5}}\end{aligned}}$

二次方程公式

**二次方程公式**指出：

$ax^{2}+bx+c\iff x={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}\quad (a\neq 0)$

例如：求解 $6x^{2}+x-9=0$

${\begin{aligned}6x^{2}+x-9=0\\x={\frac {-1\pm {\sqrt {1^{2}-4(6)(-9)}}}{2(6)}}\\x={\frac {-1\pm {\sqrt {1^{2}+216}}}{12}}\\x=(-1+{\sqrt {217}})/12\ or\ (-1-{\sqrt {217}})/12\end{aligned}}$

你可能已经注意到平方根下的部分是判别式。这是有道理的，因为如果判别式为负，则平方根不能得到实数，因此没有实根。如果判别式为零，则$x=-b/2a$，因此有一个重复根。这留下了判别式为正的情况，导致两个实根。

联立方程求解

有时我们需要求解包含线性方程和二次方程的联立方程。为了求解它们，我们需要使用代入法。

例如，求解联立方程 $x+y=-1$ 和 $x^{2}+y^{2}=25$

${\begin{aligned}x+y=-1\rightarrow &\ y=x-1\\x^{2}+y^{2}=25\rightarrow &\ x^{2}+(x-1)^{2}=25\\x^{2}+x^{2}-2x+1=25\\2x^{2}-2x-24=0&\quad {\text{Now complete the square}}\\x^{2}-x-12=0\\(x-{\frac {1}{2}})^{2}=12+{\frac {1}{4}}\\x-{\frac {1}{2}}={\sqrt {\frac {49}{4}}}\\x={\frac {1}{2}}\pm {\frac {7}{2}}\\x=-3\ or\ 4\end{aligned}}$

识别二次方程

有时二次方程会以其他形式隐藏。如果你可以进行代换将表达式转换为二次方程，你就可以像求解二次方程一样求解它。

例如，求解 $6x=1-{\sqrt {x}}$ 中 x 的值

${\begin{aligned}Let\ s={\sqrt {x}}\\6s^{2}=1-s\\6s^{2}+s-1=0\\s^{2}+{\frac {s}{6}}-{\frac {1}{6}}=0\\(s+{\frac {1}{12}})^{2}={\frac {1}{6}}+{\frac {1}{144}}\\s+{\frac {1}{12}}={\sqrt {{\frac {24}{144}}+{\frac {1}{144}}}}\\s={\frac {-1}{12}}\pm {\sqrt {\frac {25}{144}}}\\s={\frac {-1}{12}}\pm {\frac {5}{12}}\\s={\frac {-1}{2}}\ or\ {\frac {1}{3}}\\{\sqrt {x}}={\frac {-1}{2}}\ or\ {\frac {1}{3}}\\x={\frac {1}{4}}\ or\ {\frac {1}{9}}\end{aligned}}$