A-level 数学/OCR/M3/SHM

SHM 运动方程

定义运动方程（关于加速度和位移）

根据定义，当一个粒子执行简谐运动 (SHM) 时

• 它的加速度大小 ${\ddot {x}}$ 与 它的位移大小 $x$ 从某个固定点，成正比，并且
• 它的加速度和位移方向相反。

更正式地说，当运动方程 ${\ddot {x}}=-kx$ 成立时，就会发生 SHM，其中 $k$ 是一个正常数。按照惯例，我们写 $k=\omega ^{2}$（我们将稍后解释 $\omega$ 的意义）因此方程变为 ${\ddot {x}}=-\omega ^{2}x$.

在现实世界中很容易找到简谐振荡器。附着在弹性弦或弹簧上的质量的无阻尼振荡只是力学领域的一个例子。在研究这些例子之前，让我们首先使用下面描述的抽象模型来检查 SHM 的特征。

考虑以下具有 $a$ 振荡幅度 的振荡器。令 $x$ 表示它相对于原点的位移，${\ddot {x}}$ 表示它的加速度。

让我们重新说明 SHM 的定义方程

${\ddot {x}}=-\omega ^{2}x\,$

回想一下，表示位移及其关于时间的导数的代数变量表示一维矢量量（即它们都位于一条直线上）。如果变量的值为正，则其向量指向正方向；如果为负，则其向量指向另一个方向。

观察当 $x=0$ 时，则 ${\ddot {x}}=0$。根据牛顿第二定律，此时作用在振荡器上的合力 $F$ 为零。

当 $x>0$（即原点右侧）时，合力指向左侧，指向原点。当 $x<0$ 时，合力指向右侧，指向原点。因为当振荡器不在原点时，合力总是指向原点，所以合力可以被称为恢复力。恢复力的行为表明振荡器的速度在原点最大，在两个方向改变的端点（即当 $v=0$ 时，$x=\pm a$）为零。

运动方程，关于速度、振幅和位移

现在，让我们用速度 $v$ 和位移 $x$ 来改写定义的 SHM 方程。我们进行以下替换：${\ddot {x}}={\frac {dv}{dt}}={\frac {dv}{dx}}{\frac {dx}{dt}}=v{\frac {dv}{dx}}$。因此，

	${\ddot {x}}$	$=-\omega ^{2}x\,$
$\Rightarrow$	$v{\frac {dv}{dx}}$	$=-\omega ^{2}x\,$
$\Rightarrow$	$\int v\,dv$	$=-\omega ^{2}\int x\,dx$（分离变量）

用 $v=0$ 和 $x=\pm a$ 作为积分的一对极限，我们得到

	$\int _{0}^{v}v\,dv$	$=-\omega ^{2}\int _{\pm a}^{x}x\,dx$
$\Rightarrow$	$\left[{\frac {1}{2}}v^{2}\right]_{0}^{v}$	$=-\omega ^{2}\left[{\frac {1}{2}}x^{2}\right]_{\pm a}^{x}$

$\Rightarrow$

$v^{2}=\omega ^{2}(a^{2}-x^{2})\,$

现在，很明显当 $x=0$ 时（在这种情况下 $v=\pm \omega a$），速度达到最大值，而当 $x=\pm a$ 时 $v=0$。

运动方程，根据位移、振幅和时间

常数 $\omega$ 的重要性将在我们用位移 $x$ 和时间 $t$ 表示定义的 SHM 方程后变得清晰。

	${\ddot {x}}$	$=-\omega ^{2}x\,$
$\Rightarrow$	${\frac {d^{2}x}{dt^{2}}}+\omega ^{2}x$	$=0\,$

这只是一个具有常数系数的二阶常微分方程。特征方程（作为 $m$ 的函数）由下式给出：

$m^{2}+\omega ^{2}=0\Rightarrow m=\pm {\sqrt {-\omega ^{2}}}\Rightarrow m=\pm \mathrm {i} \omega$

因此，微分方程的通解可以写成

$x=A_{1}\cos(\omega t)+A_{2}\sin(\omega t)\,$，或等效地，$x=A_{3}\cos(\omega t+\varepsilon )\,$。

为了求解常数对 $\{A_{1},A_{2}\}$ 或 $\{A_{3},\varepsilon \}$，我们需要一对描述 SHM 的初始条件。

如果粒子从最大位移 $x=a$静止开始，那么我们将 $x=a$ 和 ${\frac {dx}{dt}}=0$ 代入到 $t=0$，得到 $A_{1}=a$，$A_{2}=0$ 和 $A_{3}=a$，$\varepsilon =0$。解变为 $x=a\cos(\omega t)\,$。

另一方面，如果振荡从最小位移开始，那么我们将得到 $x=a\sin(\omega t)=a\cos \left(\omega t-{\frac {\pi }{2}}\right)\,$。

一般来说，我们有

$x=a\cos(\omega t+\varepsilon )\,$

其中常数 $\varepsilon$ 取决于振荡器的起始位置。

这些方程式表明 $\omega$ 仅仅是与简谐运动相关的 恒定角速度（或角频率）。下图说明了简谐运动和 匀速圆周运动（角速度为 $\omega$）之间的关系。简谐振子的位移 $x$ 实际上只是执行匀速圆周运动的粒子的 $x$ 坐标。因此，我们可以将简谐运动视为匀速圆周运动在圆的直径上的投影。

简谐振子每经过两次端点间的距离（即距离 $4a$）就完成 一次振荡。这对应于匀速圆周运动中 一次旋转。因此，简谐运动的 振荡周期 由下式给出

$T={\frac {2\pi }{\omega }}\,$

示例：弹性弦上的质量

我们希望确定悬挂在轻质（即无质量）弹性弦上的质量是否会表现出简谐运动。

考虑一根 自然长度 为 $l$，弹性模量 为 $\lambda$ 的轻质弹性弦，从固定点 O 垂直悬挂。弦的另一端连接到 质量 为 $m$ 的粒子。

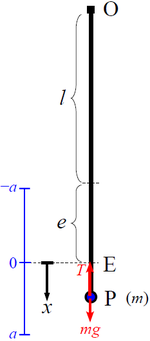
设点 E 表示粒子的 平衡位置。在 E 点，粒子处于静止状态（即作用在其上的合力为零）。设 $e$ 表示粒子位于 E 点时弦的伸长量。考虑作用在粒子上的竖直力，得到

${\frac {\lambda }{l}}e=mg\Rightarrow e={\frac {mgl}{\lambda }}$.

质量的位移 $x$ 始终从平衡位置 E 测量，因为这是 ${\ddot {x}}=0$ 且因此合力 $F=0$ 的点。

假设质量经历了一个小的位移 $x$。应用 牛顿第二定律，得到

	$mg-T$	$=m{\ddot {x}}$
$\Rightarrow$	$mg-{\frac {\lambda }{l}}(e+x)$	$=m{\ddot {x}}$
$\Rightarrow$	$mg-{\frac {\lambda }{l}}e-{\frac {\lambda }{l}}x$	$=m{\ddot {x}}$
$\Rightarrow$	$-{\frac {\lambda }{l}}x$	$=m{\ddot {x}}$ (since $mg={\frac {\lambda }{l}}e$)
$\Rightarrow$	${\ddot {x}}$	$=-{\frac {\lambda }{ml}}x$

这是简谐运动的定义运动方程，其中 $\omega ^{2}={\frac {\lambda }{ml}}$。请注意，只有当绳子保持绷紧时，即 $a<e$，粒子才能进行简谐运动。

总结

您需要知道以下公式，因为考试中不会提供这些公式。

公式	描述
${\ddot {x}}=-\omega ^{2}x$	简谐运动的定义运动方程（用加速度和位移表示）
$v^{2}=\omega ^{2}\left(a^{2}-x^{2}\right)$	简谐运动的运动方程，用速度、振幅和位移表示
$x=a\cos(\omega t+\varepsilon )\$	简谐运动的运动方程，用位移、振幅和时间表示
$T={\frac {2\pi }{\omega }}$	简谐运动的振荡周期