A 级物理学（高级物理学）/玻尔兹曼因子

气体中的粒子由于彼此之间的碰撞而随机地失去和获得能量。 平均而言，对于大量的粒子，具有至少一定能量 ε 的粒子的比例是恒定的。 这被称为玻尔兹曼因子。 它是一个介于 0 到 1 之间的值。 玻尔兹曼因子由以下公式给出

${\frac {n}{n_{0}}}=e^{\frac {-\epsilon }{kT}}$,

其中 n 是动能高于能量水平 ε 的粒子数量，n₀ 是气体中粒子的总数，T 是气体的温度（以开尔文为单位），k 是玻尔兹曼常数（1.38 x 10⁻²³ JK⁻¹）。

这种能量可以是粒子可能具有的任何类型的能量 - 例如，它可以是重力势能或动能。

推导

在大气中，粒子受到重力向下拉。 由于彼此之间的碰撞，它们获得和失去重力势能 (mgh)。 首先，让我们考虑一小块大气。 它具有水平横截面积 A，高度 dh，分子密度（每单位体积的分子数）n，并且所有分子都具有质量 m。 令块中的粒子数为 N。

$n={\frac {N}{V}}={\frac {N}{A\;dh}}$

所以

$V=A\;dh$（如果你仔细想想，这是有道理的）

根据定义

$N=nV=nA\;dh$

总质量 Σ m 是单个分子的质量 (m) 乘以分子数量 (N)

$\Sigma m=mN=mnA\;dh$

然后计算块的重量

$W=g\Sigma m=nmgA\;dh$

向下的压力 P 是每单位面积的力，因此

$P={\frac {W}{A}}={\frac {nmgA\;dh}{A}}=nmg\;dh$

我们知道，当我们在大气中上升时，压力会下降。 因此，在我们的小块中，存在由以下公式给出的压力差 dP

$dP=-nmg\;dh$（1）换句话说，压力正在下降 (-)，它是这一小块大气重量的结果。

我们也知道

$PV=NkT$

所以

$P={\frac {NkT}{V}}$

但是

$n={\frac {N}{V}}$

所以，通过替换

$P=nkT$

所以，对于我们的小块

$dP=kT\;dn$ (2)

如果我们将 (1) 和 (2) 等同

$dP=-nmg\;dh=kT\;dn$

重新排列以获得

${\frac {dn}{dh}}={\frac {-nmg}{kT}}$

${\frac {dh}{dn}}={\frac {-kT}{nmg}}$

在 n₀ 和 n 的极限之间积分

$h={\frac {-kT}{mg}}\int _{n_{0}}^{n}{\frac {1}{n}}\;dn={\frac {-kT}{mg}}\left[\ln {n}\right]_{n_{0}}^{n}={\frac {-kT}{mg}}\left(\ln {n}-\ln {n_{0}}\right)={\frac {-kT}{mg}}\ln {\frac {n}{n_{0}}}$

$ln{\frac {n}{n_{0}}}={\frac {-mgh}{kT}}$

${\frac {n}{n_{0}}}=e^{\frac {-mgh}{kT}}$

由于我们正在处理重力势能，ε = mgh，所以

${\frac {n}{n_{0}}}=e^{\frac {-\epsilon }{kT}}$

此函数的图表

此主题在 2010 年 6 月 Q10 494 中出现。该问题中使用的各种值的数值为

$k=1.4\times 10^{-23}JK^{-1},~g=9.8,~m=4.9\times 10^{-26}Kg,~T=290K$

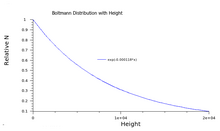显示如何通过高度获得能量

问题

1u = 1.66 x 10⁻²⁷ kg

g = 9.81 ms⁻²

$k=1.38\times 10^{-23}$

1. 氮气分子的分子量为 28u。如果地球大气层是 100% 氮气，温度为 18 °C，那么有多少比例的氮气分子能达到 2 km 的高度？

2. 在 0 °C 下，一箱氢气（分子量为 2u）中，有多少比例的分子速度大于 5ms⁻¹？

3. 如果一半的氢气以至少 10ms⁻¹ 的速度运动，那么氢气的温度是多少？

4. 一些电离的氢气（电荷 -1.6 x 10⁻¹⁹ C）放置在均匀的电场中。两极板之间的电位差为 20V，两极板之间的距离为 1m。在 350°K 的情况下，有多少比例的分子距离正极板至少 0.5m（忽略重力）？

解题步骤