考虑一个从静止状态以恒定加速度 1g 加速的火箭。考虑到相对论效应,我们实际上指的是什么?显然,火箭不能以恒定速率增加速度(对于保持静止的人来说),因为它最终会超过光速。实际上发生的是,火箭以指数方式接近光速,如下所示。
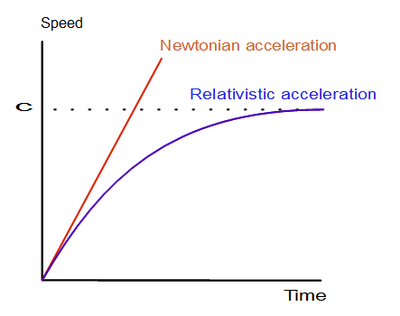 相对论加速度和牛顿加速度
相对论加速度和牛顿加速度
那么我们指的是恒定加速度什么呢?好吧,从船上宇航员的角度来看,我们指的是他们体验到一个恒定的模拟重力场,该重力场是由持续燃烧的火箭发动机的稳定推力产生的,这与地球上的 1g 感受完全一样。对他们来说,宇宙飞船永远处于静止状态,但船外的宇宙看起来以越来越快的速度经过,就像上面的插图一样。
现在,我们似乎需要在这里使用广义相对论的概念,但实际上没有必要。我们只需要仔细定义我们指的是这种加速度的哪种类型。在牛顿世界中,如果以速度 v 运动的物体以加速度 a 加速一小段时间 δt,则最终速度由下式给出

|
然而,在相对论世界中,我们必须使用相对论速度叠加公式(见附录 *),即

|
这导致

|

|
消去二阶项,我们得到

|

|
现在我们所要做的就是对这个表达式进行积分,以找出 v 如何随 t 变化。首先分离变量

|

|
现在积分

|
幸运的是,这是一个标准积分,我的数学书告诉我它是

|
(由于 v 在 t = 0 时为 0,因此没有积分常数)。一些简单的操作可以让我们得到第一个结果

|
注意这里提到的时间 t 是 proper time 的积分,也就是行程时间 - 也就是飞船上的乘客所经历的时间。所以这个公式告诉你经过时间 t 后你的速度会是多少。
接下来,我们想知道在这段时间内你能走多远。为了做到这一点,我们必须考虑到越快,你经过的距离就越缩短!在牛顿世界中,在短时间 δt 内以速度 v 行驶的距离 δs 为

|
但在相对论世界中,你实际上走得更远,因为飞船外所有的距离都因 γ 倍的长度收缩,所以

|

|
将我们经过时间 t 后飞船速度的公式代入,我们得到

|

|
对这个表达式进行积分,得到

|
这次我们不能忽略积分常数,因为当 t = 0 时,s = 0,但 cosh(0) 为 1 而不是零。因此,最终结果为

|
我们想了解的第三件事是,我们回来的时候我们的朋友会多大岁数!好吧,对于我们以速度 v 行驶的每一秒,留在地球上的朋友会老 γ 秒,即

|

|

|
由此,我们得到

|
(积分常数为零,因为 sinh(0) = 0,正如预期的那样)
我发现 1g 火箭问题的解拥有如此简单而优雅的答案,尤其是在我们使用年和光年进行计算时,这一点特别令人满意。在这些单位中,a 和 c 都等于 1。如果我们考虑一个往返行程,该行程需要 T 年(以飞船上的时间测量),那么往程将包含两个阶段,加速阶段持续 T/4 年,减速阶段同样长。返程也一样。
达到的最大速度将是

|
你将到达的距离是

|
当你回来时,你刚出生的小儿子的年龄将是

|
为了让你了解这些表达式在实际应用中的样子,这里有一个结果表
| 旅程时间 (年) |
最大速度 (% of c) |
距离 (光年) |
儿子年龄 (年) |
| 0 |
0 |
0 |
0
|
| 1 |
24 |
0.1 |
1
|
| 2 |
46 |
0.3 |
2
|
| 3 |
64 |
0.6 |
3
|
| 4 |
76 |
1.1 |
5
|
| 5 |
85 |
2 |
6
|
| 6 |
91 |
3 |
9
|
| 7 |
94 |
4 |
11
|
| 8 |
96 |
6 |
15
|
| 9 |
98 |
8 |
19
|
| 10 |
99 |
10 |
24
|
值得注意的是,理论上往返一颗距离地球10光年的恒星只需要10年的宇航员时间 (而地球上已经过去了24年)。如果你准备旅行20年、30年或40年,你可以分别到达距离地球150光年、1800光年和22000光年的恒星 (这相当于银河系四分之一的距离!) 如果你不介意不回家,你可以在仅仅47年内到达已知宇宙的边缘 (不过,当你到达那里时,宇宙是否还存在就是另一个问题了!)
回到引言...
回到顶部...


























