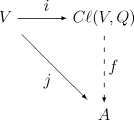抽象代数/克利福德代数

在数学中，克利福德代数是一种结合代数。它们可以被认为是复数和四元数的一种可能的推广。克利福德代数的理论与二次型和正交变换的理论密切相关。克利福德代数在各种领域有重要的应用，包括几何和理论物理。它们以英国几何学家威廉·克利福德的名字命名。

阅读本节时，对多线性代数的基本知识有所了解将很有用。

介绍和基本性质

具体而言，克利福德代数是一个幺结合代数，它包含并由向量空间 V 生成，该向量空间配备了二次型 Q。克利福德代数 Cℓ(V,Q) 是由 V 生成的“最自由”的代数，受以下条件约束¹

$v^{2}=Q(v)\ {\mbox{ for all }}v\in V.$

如果底域 K 的特征不为 2，那么可以将这个基本恒等式改写成以下形式

$uv+vu=\langle u,v\rangle {\mbox{ for all }}u,v\in V,$

其中 <u, v> = Q(u + v) − Q(u) − Q(v) 是与 Q 相关的对称双线性形式。这种“最自由”或“最一般”的代数受此恒等式约束的想法可以通过泛性质的概念来正式表达（见下文）。

克利福德代数与外代数密切相关。事实上，如果 Q = 0，那么克利福德代数 Cℓ(V,Q) 仅仅是外代数 Λ(V)。对于非零 Q，当底域 K 的特征不为二时，Λ(V) 和 Cℓ(V,Q) 之间存在一个规范的线性同构。也就是说，它们作为向量空间自然同构，但具有不同的乘法（在特征为二的情况下，它们仍然作为向量空间同构，只是不是自然同构）。克利福德乘法严格来说比外积更丰富，因为它利用了 Q 提供的额外信息。更准确地说，可以将它们看作是外代数的量子化，就像韦尔代数是对称代数的量子化一样。

特征为 2 的二次型和克利福德代数构成了一个特殊情况。特别是，如果 char K = 2，那么二次型是由其对称双线性形式决定的，或者每个二次型都承认正交基，这是不成立的。本文中的许多陈述都包含特征不为 2 的条件，如果去除此条件，这些陈述就会失效。

泛性质和构造

令 V 是域 K 上的向量空间，令 Q : V → K 是 V 上的二次型。在大多数感兴趣的情况下，域 K 要么是 R 要么是 C（特征为 0）或者是一个有限域。

克利福德代数 Cℓ(V,Q) 是 K 上的一个幺结合代数，以及一个线性映射 i : V → Cℓ(V,Q)，由以下泛性质定义：给定 K 上的任何结合代数 A 和任何线性映射 j : V → A，使得

j(v)² = Q(v)1 对于所有 v ∈ V

（其中 1 表示 A 的乘法单位元），存在唯一的代数同态 f : Cℓ(V,Q) → A，使得以下图表可交换（即，使得 f o i = j）

使用对称双线性形式 <·,·> 而不是 Q（在特征不为 2 的情况下），对 j 的要求是

j(v)j(w) + j(w)j(v) = <v, w> 对于所有 v, w ∈ V。

如上所述的克利福德代数始终存在，并且可以通过以下方式构建：从包含 V 的最一般代数开始，即张量代数 T(V)，然后通过取合适的商来强制基本恒等式。在我们的例子中，我们要取 T(V) 中由所有形式为

$v\otimes v-Q(v)1$ 对于所有 $v\in V$

的所有元素生成的双边理想 I_Q

并定义 Cℓ(V,Q) 为商

Cℓ(V,Q) = T(V)/I_Q.

然后很容易证明 Cℓ(V,Q) 包含 V 并且满足上述泛性质，因此 Cℓ 在同构意义上是唯一的；因此人们谈论“克利福德代数”Cℓ(V, Q)。从这个构造中也得出 i 是单射的。人们通常会省略 i 并将 V 视为 Cℓ(V,Q) 的一个线性子空间。

克利福德代数的泛性质表明 Cℓ(V,Q) 的构造本质上是函子性的。也就是说，Cℓ 可以被看作是从配备了二次型的向量空间范畴（其态射是保持二次型的线性映射）到结合代数范畴的函子。泛性质保证向量空间之间的线性映射（保持二次型）唯一地扩展到相关克利福德代数之间的代数同态。

[编辑 | 编辑源代码]

$\{e_{i_{1}}e_{i_{2}}\cdots e_{i_{k}}\mid 1\leq i_{1}<i_{2}<\cdots <i_{k}\leq n{\mbox{ and }}0\leq k\leq n\}$

是 Cℓ(V,Q) 的一个基。空乘积 (k = 0) 定义为乘法单位元。对于每个 k 值，有 n 选择 k 个基元，所以克利福德代数的总维数为

$\dim C\ell (V,Q)=\sum _{k=0}^{n}{\begin{pmatrix}n\\k\end{pmatrix}}=2^{n}.$

由于 V 配备了二次型，因此 V 有一组特权基：正交基。正交基是指满足以下条件的基

$\langle e_{i},e_{j}\rangle =0\qquad i\neq j.\,$

其中 <·,·> 是与 Q 相关的对称双线性形式。基本克利福德恒等式意味着对于正交基，有

$e_{i}e_{j}=-e_{j}e_{i}\qquad i\neq j.\,$

这使得正交基向量的操作非常简单。给定一个 $e_{i_{1}}e_{i_{2}}\cdots e_{i_{k}}$ 的乘积，其中 e _i 是 不同 的正交基向量，可以通过包含一个与正确排序所需的翻转次数（即排序置换的符号）相对应的总符号将它们按标准顺序排列。

如果特征不是 2，则 V 存在正交基，并且可以轻松地将 V 上的二次型扩展到 Cℓ(V,Q) 上的二次型，要求当 {e _i} 是正交的时，不同的元 $e_{i_{1}}e_{i_{2}}\cdots e_{i_{k}}$ 彼此正交。此外，我们设置

$Q(e_{i_{1}}e_{i_{2}}\cdots e_{i_{k}})=Q(e_{i_{1}})Q(e_{i_{2}})\cdots Q(e_{i_{k}})$.

标量的二次型只是 Q(λ) = λ²。因此， V 的正交基扩展到 Cℓ(V,Q) 的正交基。以这种方式定义的二次型实际上独立于所选择的正交基（稍后将给出基无关的公式）。

示例：实克利福德代数和复克利福德代数

最重要的克利福德代数是在配备了非退化二次型的实向量空间和复向量空间上的克利福德代数。

有限维实向量空间上的每个非退化二次型都等价于标准对角形式

$Q(v)=v_{1}^{2}+\cdots +v_{p}^{2}-v_{p+1}^{2}-\cdots -v_{p+q}^{2}$

其中 n = p + q 是向量空间的维数。整数对 (p, q) 称为二次型的符号。具有此二次型的实向量空间通常表示为 R^p,q。R^p,q 上的克利福德代数表示为 Cℓ_p,q(R)。符号 Cℓ_n(R) 表示 Cℓ_n,0(R) 或 Cℓ_0,n(R)，具体取决于作者更喜欢正定空间还是负定空间。

R^p,q 的标准正交基 {e _i} 由 n = p + q 个相互正交的向量组成，其中 p 个向量的范数为 +1， q 个向量的范数为 -1。因此，代数 Cℓ_p,q(R) 将有 p 个向量平方为 +1， q 个向量平方为 -1。

注意，Cℓ_0,0(R) 自然同构于 R，因为没有非零向量。Cℓ_0,1(R) 是由单个向量 e₁ 生成的二维代数，它平方为 −1，因此同构于 C，即复数域。代数 Cℓ_0,2(R) 是一个由 {1, e₁, e₂, e₁e₂} 张成的四维代数。后三个元素平方为 −1，并且全部反交换，因此该代数同构于四元数 H。序列中的下一个代数是 Cℓ_0,3(R)，它是一个 8 维代数，同构于称为克利福德双四元数的直和 H ⊕ H。

我们也可以研究复向量空间上的克利福德代数。复向量空间上的每个非退化二次型都等价于标准对角形式

$Q(z)=z_{1}^{2}+z_{2}^{2}+\cdots +z_{n}^{2}$

其中 n = dim V，因此本质上每个维度只有一个克利福德代数。我们将用标准二次型在 Cⁿ 上的克利福德代数记为 Cℓ_n(C)。可以证明代数 Cℓ_n(C) 可以通过代数 Cℓ_p,q(R) 的复化获得，其中 n = p + q

$C\ell _{n}(\mathbb {C} )\cong C\ell _{p,q}(\mathbb {R} )\otimes \mathbb {C} \cong C\ell (\mathbb {C} ^{p+q},Q\otimes \mathbb {C} )$.

这里 Q 是签名为 (p,q) 的实二次型。注意，复化不依赖于签名。前几个情况并不难计算。我们发现

Cℓ₀(C) = C

Cℓ₁(C) = C ⊕ C

Cℓ₂(C) = M₂(C)

其中 M₂(C) 表示 C 上的 2×2 矩阵代数。

事实证明，每个代数 Cℓ_p,q(R) 和 Cℓ_n(C) 都同构于 R、C 或 H 上的矩阵代数，或者同构于两个这样的代数的直和。有关这些代数的完整分类，请参见克利福德代数的分类。

性质

与外代数的关系

给定一个向量空间 V，我们可以构造外代数 Λ(V)，其定义独立于 V 上的任何二次型。事实证明，如果 F 的特征不为 2，则 Λ(V) 和 Cℓ(V,Q) 之间存在一个自然同构，它们被认为是向量空间（并且在特征为 2 时存在一个同构，它可能不是自然的）。当且仅当 Q = 0 时，这是一个代数同构。因此，我们可以将克利福德代数 Cℓ(V,Q) 视为对 V 上的外代数的丰富（或者更准确地说，是量化，参见引言），其中乘法取决于 Q（我们仍然可以独立于 Q 定义外积）。

建立同构的最简单方法是为 V 选择一个正交基 {e_i}，并将其扩展为 Cℓ(V,Q) 的正交基，如上所述。映射 Cℓ(V,Q) → Λ(V) 由以下决定

$e_{i_{1}}e_{i_{2}}\cdots e_{i_{k}}\mapsto e_{i_{1}}\wedge e_{i_{2}}\wedge \cdots \wedge e_{i_{k}}.$

注意，这只有在基 {e_i} 正交时才有效。可以证明这个映射独立于正交基的选择，因此它给出了一个自然同构。

如果 K 的特征为 0，我们还可以通过反对称化建立同构。定义函数 f_k : V × … × V → Cℓ(V,Q) 为

$f_{k}(v_{1},\cdots ,v_{k})={\frac {1}{k!}}\sum _{\sigma \in S_{k}}{\rm {sgn}}(\sigma )\,v_{\sigma (1)}\cdots v_{\sigma (k)}$

其中求和是对 k 个元素的对称群求和。由于 f_k 是交错的，因此它诱导了一个唯一的线性映射 Λ^k(V) → Cℓ(V,Q)。这些映射的直接和给出了 Λ(V) 和 Cℓ(V,Q) 之间的线性映射。可以证明这个映射是一个线性同构，而且它是自然的。

更复杂的方法是构建 Cℓ(V,Q) 上的过滤。回想一下，张量代数 T(V) 具有一个自然过滤：F⁰ ⊂ F¹ ⊂ F² ⊂ … 其中 F^k 包含秩 ≤ k 的张量的和。将它投影到克利福德代数上，就会在 Cℓ(V,Q) 上产生一个过滤。相关的分级代数

$\bigoplus _{k}F^{k}/F^{k-1}$

自然同构于外代数 Λ(V)。由于滤波代数的关联分级代数总是作为滤波向量空间与滤波代数同构（通过为所有 k 选择 F^k 在 F^k+1 中的补集），这提供了一种同构（尽管不是自然的同构），在任何特征中，甚至在特征二中。

分级

由 $v\mapsto -v$ 定义的 V 上的线性映射保留了二次型 Q，因此根据克利福德代数的泛性质扩展到代数自同构

α : Cℓ(V,Q) → Cℓ(V,Q)。

由于 α 是一个对合（即它平方为恒等式），人们可以将 Cℓ(V,Q) 分解为正特征空间和负特征空间

$C\ell (V,Q)=C\ell ^{0}(V,Q)\oplus C\ell ^{1}(V,Q)$

其中 Cℓⁱ(V,Q) = {x ∈ Cℓ(V,Q) | α(x) = (−1)ⁱx}。由于 α 是一个自同构，因此得出

$C\ell ^{\,i}(V,Q)C\ell ^{\,j}(V,Q)=C\ell ^{\,i+j}(V,Q)$

其中上标以模 2 阅读。这意味着 Cℓ(V,Q) 是一个 Z₂-分级代数（也称为超代数）。请注意，Cℓ⁰(V,Q) 构成 Cℓ(V,Q) 的一个子代数，称为 **偶子代数**。部分 Cℓ¹(V,Q) 称为 Cℓ(V,Q) 的 **奇数部分**（它不是子代数）。这个 Z₂-分级在克利福德代数的分析和应用中起着重要作用。自同构 α 称为 **主对合** 或 **等级对合**。

备注。在特征不为 2 的情况下，代数 Cℓ(V,Q) 从与外代数 Λ(V) 的规范同构继承了一个 Z-分级。然而，重要的是要注意，这只是一个 向量空间分级。也就是说，克利福德乘法不尊重 Z-分级，只尊重 Z₂-分级。令人高兴的是，分级以自然的方式相关：Z₂ = Z/2Z。克利福德数的 度数 通常指的是 Z-分级中的度数。在 Z₂-分级中纯粹的元素被称为偶数或奇数。

如果 F 的特征不为 2，则克利福德代数的偶子代数 Cℓ⁰(V,Q) 本身就是一个克利福德代数。如果 V 是范数为 Q(a) 的向量 a 和子空间 U 的正交直和，则 Cℓ⁰(V,Q) 同构于 Cℓ(U,−Q(a)Q)，其中 −Q(a)Q 是 Q 限制到 U 并乘以 −Q(a) 的形式。特别是在实数上，这意味着

$C\ell _{p,q}^{0}(\mathbb {R} )\cong C\ell _{p,q-1}(\mathbb {R} )$ 对于 q > 0，以及

$C\ell _{p,q}^{0}(\mathbb {R} )\cong C\ell _{q,p-1}(\mathbb {R} )$ 对于 p > 0。

在负定情况下，这给出了一个包含 Cℓ_0,n−1(R) ⊂ Cℓ_{0, n}(R)，它扩展了序列

R ⊂ C ⊂ H ⊂ H⊕H ⊂ …

同样，在复数情况下，可以证明 Cℓ_n(C) 的偶子代数同构于 Cℓ_n−1(C)。

反对合

除了自同构 α 之外，还有两个反对合在克利福德代数的分析中起着重要作用。回想一下，张量代数 T(V) 带有一个反对合，它反转所有乘积中的顺序

$v_{1}\otimes v_{2}\otimes \cdots \otimes v_{k}\mapsto v_{k}\otimes \cdots \otimes v_{2}\otimes v_{1}$.

由于理想的 I_Q 在此反转下是不变的，此操作下降为 Cℓ(V,Q) 的一个反自同构，称为转置或反转操作，用 x^t 表示。转置是一个反自同构：$(xy)^{t}=y^{t}x^{t}$。转置操作不使用Z₂-分级，因此我们通过组合 α 和转置来定义第二个反自同构。我们将此操作称为克利福德共轭，用 ${\bar {x}}$ 表示。

${\bar {x}}=\alpha (x^{t})=\alpha (x)^{t}.$

在这两个反自同构中，转置是最基本的。³

注意，所有这些操作都是对合。可以证明，它们在Z-分级中纯净的元素上作用为 ±1。事实上，所有三个操作都只依赖于模 4 的度数。也就是说，如果 x 是纯净的，度数为 k，那么

$\alpha (x)=\pm x\qquad x^{t}=\pm x\qquad {\bar {x}}=\pm x$

其中符号由下表给出

k mod 4	0	1	2	3
$\alpha (x)\,$	+	−	+	−	(−1)k
$x^{t}\,$	+	+	−	−	(−1)k(k−1)/2
${\bar {x}}$	+	−	−	+	(−1)k(k+1)/2

克利福德标量积

当特征不为 2 时，V 上的二次型 Q 可以扩展到 Cℓ(V,Q) 的所有部分，如前所述（我们也用 Q 表示）。一个与基无关的定义是

$Q(x)=\langle x^{t}x\rangle$

其中 <a> 表示 a 的标量部分（Z-分级中的 0 级部分）。可以证明

$Q(v_{1}v_{2}\cdots v_{k})=Q(v_{1})Q(v_{2})\cdots Q(v_{k})$

其中 v_i 是 V 的元素 - 对于 Cℓ(V,Q) 的任意元素，此恒等式不成立。

Cℓ(V,Q) 上相关的对称双线性形式由下式给出

$\langle x,y\rangle =\langle x^{t}y\rangle .$

可以检查到，当限制在 V 上时，这将简化为原始的双线性形式。Cℓ(V,Q) 上的双线性形式是非退化的，当且仅当它在 V 上是非退化的。

不难验证转置是关于此内积的左/右克利福德乘法的伴随。也就是说，

$\langle ax,y\rangle =\langle x,a^{t}y\rangle ,$ 以及

$\langle xa,y\rangle =\langle x,ya^{t}\rangle .$

克利福德代数的结构

在本节中，我们假设向量空间 V 是有限维的，并且 Q 的双线性形式是非奇异的。K 上的中心简单代数是具有中心 K 的（有限维）除代数上的矩阵代数。例如，实数上的中心简单代数是实数或四元数上的矩阵代数。

• 如果 V 的维数为偶数，那么 Cℓ(V,Q) 是 K 上的中心简单代数。
• 如果 V 的维数为偶数，那么 Cℓ⁰(V,Q) 是 K 的二次扩张上的中心简单代数，或者 K 上两个同构中心简单代数的总和。
• 如果 V 的维数为奇数，那么 Cℓ(V,Q) 是 K 的二次扩张上的中心简单代数，或者 K 上两个同构中心简单代数的总和。
• 如果 V 的维数为奇数，那么 Cℓ⁰(V,Q) 是 K 上的中心简单代数。

克利福德代数的结构可以使用以下结果明确地计算出来。假设 U 的维数为偶数，并且具有判别式为 d 的非奇异双线性形式，并且假设 V 是另一个具有二次形式的向量空间。U+V 的克利福德代数同构于 U 和 (−1)^dim(U)/2dV 的克利福德代数的张量积，即其二次形式乘以 (−1)^dim(U)/2d 的空间 V。在实数上，这尤其意味着

$Cl_{p+2,q}(\mathbb {R} )=M_{2}(\mathbb {R} )\otimes Cl_{q,p}(\mathbb {R} )$

$Cl_{p+1,q+1}(\mathbb {R} )=M_{2}(\mathbb {R} )\otimes Cl_{p,q}(\mathbb {R} )$

$Cl_{p,q+2}(\mathbb {R} )=\mathbb {H} \otimes Cl_{q,p}(\mathbb {R} )$

这些公式可用于查找所有实克利福德代数的结构。

克利福德群 Γ

在本节中，我们假设 V 是有限维的，并且 Q 的双线性形式是非奇异的。

克利福德群 Γ 定义为克利福德代数中所有可逆元素 x 的集合，使得

$xv\alpha (x)^{-1}\in V$

对于所有 V 中的 v。该公式还定义了克利福德群对向量空间 V 的作用，该作用保留范数 Q，因此给出了从克利福德群到正交群的同态。克利福德群包含所有具有非零范数的 V 中的元素 r，它们通过相应的反射作用于 V，将 v 变为 v − <v,r>r/Q(r)（在特征 2 中，这些被称为正交平移而不是反射）。

许多作者对克利福德群的定义略有不同，将作用 xvα(x)⁻¹ 替换为 xvx⁻¹。这会产生相同的克利福德群，但克利福德群对 V 的作用略有改变：克利福德群的奇数元素 Γ¹ 的作用乘以一个额外的因子 -1。这里使用这种作用有几个细微的优势：它与通常的超代数符号约定一致，V 中的元素对应于反射，在奇数维中，从克利福德群到正交群的映射是满射，并且核不超过 K^*。使用作用 α(x)vx⁻¹ 而不是 xvα(x)⁻¹ 不会造成任何区别：它会产生具有相同 V 作用的相同克利福德群。

克利福德群 Γ 是两个子集 Γ⁰ 和 Γ¹ 的不相交并集，其中 Γⁱ 是度数为 i 的元素的子集。子集 Γ⁰ 是 Γ 中指数为 2 的子群。

如果 V 是具有非退化双线性形式的有限维的，那么克利福德群映射到 V 的正交群，并且核由域 K 中的非零元素组成。这会导致精确序列

$1\rightarrow K^{*}\rightarrow \Gamma \rightarrow O_{V}(K)\rightarrow 1,\,$

$1\rightarrow K^{*}\rightarrow \Gamma ^{0}\rightarrow SO_{V}(K)\rightarrow 1.\,$

在任意特征下，旋量范数 Q 在克利福德群上定义为

$Q(x)=x^{t}x\,$

这是一个从克利福德群到K的非零元素群K^*的同态。当V被识别为克利福德代数的子空间时，它与V的二次型Q一致。一些作者对旋量范数的定义略有不同，因此它与这里定义的旋量范数在Γ¹上相差一个-1、2或-2的因子。这种差异并不重要。

K的非零元素在域K的非零元素平方群K^*2中具有旋量范数。因此，当V是有限维且非奇异时，我们得到一个从V的正交群到群K^*/K^*2的诱导映射，也称为旋量范数。向量r的反射的旋量范数在K^*/K^*2中的像为Q(r)，这个性质在正交群上唯一地定义了它。这给出以下精确序列

$1\rightarrow \{\pm 1\}\rightarrow Pin_{V}(K)\rightarrow O_{V}(K)\rightarrow K^{*}/K^{*2},\,$

$1\rightarrow \{\pm 1\}\rightarrow Spin_{V}(K)\rightarrow SO_{V}(K)\rightarrow K^{*}/K^{*2}.\,$

注意，在特征为2的情况下，群{±1}只有一个元素。

旋群和Pin群

在本节中，我们假设V是有限维的，其双线性形式是非奇异的。（如果K的特征为2，这意味着V的维数是偶数。）

Pin群Pin_V(K)是克利福德群Γ中旋量范数为1的元素的子群，类似地，旋群Spin_V(K)是Pin_V(K)中迪克森不变量为0的元素的子群。当特征不为2时，这些元素的行列式为1。旋群通常在Pin群中具有指标2。

回顾上一节，克利福德群到正交群存在一个同态。我们将特殊正交群定义为Γ⁰的像。如果K的特征不为2，这仅仅是正交群中行列式为1的元素的群。如果K的特征为2，那么正交群的所有元素的行列式都为1，而特殊正交群是迪克森不变量为0的元素的集合。

从Pin群到正交群存在一个同态。它的像由旋量范数为1 ∈ K^*/K^*2的元素组成。它的核由元素+1和-1组成，并且阶数为2，除非K的特征为2。类似地，从旋群到V的特殊正交群存在一个同态。

在V是实数上的正定或负定空间的常见情况下，旋群映射到特殊正交群，并且当V的维数至少为3时是单连通的。警告：这在一般情况下并不成立：如果V是R^p,q，其中p和q都至少为2，那么旋群就不是单连通的，并且不会映射到特殊正交群。在这种情况下，代数群Spin_{p,q作为代数群是单连通的，即使其实数值点Spinp,q(R)不是单连通的。这是一个相当微妙的点，它完全混淆了至少一本关于旋群的标准书籍的作者。}

旋量

假设p+q=2n是偶数。那么克利福德代数Cℓ_p,q(C)是一个矩阵代数，因此具有一个维数为2ⁿ的复表示。通过限制到群Pin_p,q(R)，我们得到一个维数相同的Pin群的复表示，称为旋量表示。如果我们将此限制到旋群Spin_p,q(R)，那么它将分裂为两个维数为2^n-1的半旋表示（或韦尔表示）。

如果p+q=2n+1是奇数，那么克利福德代数Cℓ_p,q(C)是两个矩阵代数的和，每个矩阵代数都具有维数为2ⁿ的表示，并且这些也是Pin群Pin_p,q(R)的表示。在限制到旋群Spin_p,q(R)时，它们变得同构，因此旋群具有一个维数为2ⁿ的复旋量表示。

更一般地说，任何域上的旋群和Pin群具有类似的表示，它们的精确结构取决于相应克利福德代数的结构：每当克利福德代数有一个因子是某个除环上的矩阵代数时，我们都会得到一个相应的Pin和旋群在该除环上的表示。关于实数上的例子，请参见关于旋量的文章。

应用

微分几何

外代数的主要应用之一是在微分几何中，它被用来定义光滑流形上的微分形式丛。在（伪）黎曼流形的情况下，切空间配备了由度量诱导的自然二次型。因此，可以类比外丛定义克利福德丛。这在黎曼几何中有很多重要的应用。

物理学

克利福德代数在物理学中具有许多重要的应用。物理学家通常认为克利福德代数是一个由矩阵γ₁,…,γ_n生成的代数，这些矩阵称为狄拉克矩阵，它们具有以下性质

$\gamma _{i}\gamma _{j}+\gamma _{j}\gamma _{i}=2\eta _{ij}\,$

其中η是签名为(p,q)的二次型的矩阵——通常在闵可夫斯基空间中工作时为(1,3)。这些正是克利福德代数Cl_1,3(C)的定义关系（除了一个无关紧要的因子2），根据克利福德代数的分类，它同构于4×4复矩阵的代数。

狄拉克矩阵最早由保罗·狄拉克在尝试为电子编写一个相对论性的二阶波动方程时写下，并给出了从克利福德代数到复矩阵代数的明确同构。结果用于定义狄拉克方程。整个克利福德代数在量子场论中以狄拉克场双线性形式出现。

脚注

1. 处理实克利福德代数并偏好正定二次形式的数学家（特别是那些从事指标理论研究的数学家）有时会在基本克利福德恒等式中使用不同的符号选择。也就是说，他们采用v² = −Q(v)。在从一种约定转换为另一种约定时，必须将Q替换为−Q。
2. 当使用克利福德代数的备用 (-) 符号约定时，情况正好相反：共轭更重要。一般来说，当从一种符号约定转换为另一种符号约定时，共轭和转置的含义会互换。例如，在本文中使用的约定中，向量的逆由$v^{-1}=v^{t}/Q(v)$给出，而在 (-) 约定中，它由$v^{-1}={\bar {v}}/Q(v)$给出。

参考文献

• Carnahan, S. Borcherds Seminar Notes, Uncut. 第 5 周，"旋量和克利福德代数"。
• Lawson 和 Michelsohn，Spin Geometry，普林斯顿大学出版社。1989。 ISBN 0-691-08542-0。关于克利福德代数及其在微分几何中的应用的进阶教科书。
• Lounesto，P.，Clifford Algebras and Spinors，剑桥大学出版社。2001。 ISBN 0-521-00551-5。
• Porteous，I.，Clifford Algebras and the Classical Groups，剑桥大学出版社。1995。 ISBN 0-521-55177-3。

外部链接

• Planetmath 上关于克利福德代数的条目
• 克利福德代数的历史 （未经验证）