高级无机化学/表示

表示

表示是一组矩阵，每个矩阵对应于一个对称操作，并且以与该群中对称操作组合相同的方式进行组合。¹ 对称操作可以用矩阵表示，这让我们可以通过矩阵计算来理解对称操作之间的关系。为了理解表示，了解对称操作的矩阵概念至关重要。

以下是一些矩阵形式的对称操作示例

空间中的一个点 = ${\begin{bmatrix}x\\y\\z\end{bmatrix}}$

E = ${\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}}$

i = ${\begin{bmatrix}-1&0&0\\0&-1&0\\0&0&-1\end{bmatrix}}$

σ_xy = ${\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}}$

C_n = ${\begin{bmatrix}cos\theta &-sin\theta &0\\sin\theta &cos\theta &0\\0&0&1\end{bmatrix}}$(以z为主要轴)

S_n = ${\begin{bmatrix}cos\theta &-sin\theta &0\\sin\theta &cos\theta &0\\0&0&-1\end{bmatrix}}$(以z为主要轴)

对于C_n操作，θ取决于n，且关系为θ = ${\frac {360}{n}}$。如果对称性是C₂，那么θ将是180°，因为分子旋转了180°。对于C₃，θ将是120°，C₄ θ将是90°，等等。

要将对称操作应用于分子中的原子，可以将矩阵组合起来以产生该群中的另一个操作。对于像图2中所示的水这样的C_2v对称化合物，可以将操作（E、C₂、σ_v1、σ_v2）应用于向量（x、y、z）以找到表示。为了简化数学运算，可以通过对单个向量进行块对角化来进行 1x1 矩阵。

例如，

E(y) = [1] [y] = y

C₂(y) = [-1] [y] = -y

σ_v1(y) = σ_xz = [-1] [y] = -y

σ_v2(y) = σ_yz = [1] [y] = y

在这个例子中，如果你将恒等式 (E) 应用于图3 中所示的向量 y，你将得到 y。如果你将 C₂ 旋转绕主要轴应用于 y，那么你将得到 -y，等等。这些获得的结果显示了对称操作后向量的​​位置。对称操作后每个向量的系数可以用图1 中所示的字符表中的 Γ_y 表示。这组矩阵，每个矩阵对应于一个矩阵的特征，就是表示¹。相同的对称操作可以应用于 x 和 z 以获得 Γ_x 和 Γ_z 的表示。

图1. C_2v 中的 xyz 表示。

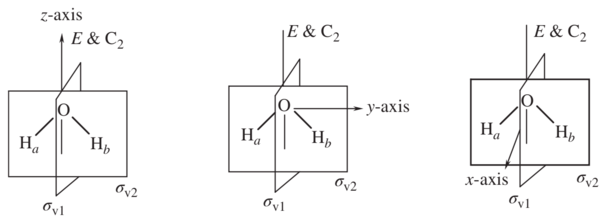
图2. 水分子 a) z轴 b) y轴 c) x轴

图 3. 直角坐标系上的 y 向量。

表示可以以与群中对称算子组合相同的方式组合，因此，表示每个对称算子的矩阵的乘法表也必须以与对称算子本身相乘相同的方式相乘。¹ 请参见图 4。

图 4. C_2v 点群的乘法表，显示 1 × 1 矩阵表示如何以与对称算子相同的方式相乘。

不可约表示和可约表示

表示可以分为不可约表示和可约表示。字符表中列出了不可约表示，它们是图 5 中蓝色阴影部分。不可约表示有 5 个规则，如下所示。

5 个规则

1. 群的不可约表示的维数的平方和等于群的阶。

h =Σ_il_i²

2. 任何不可约表示中字符的平方和等于 h。

h =Σ_i [X_i (R)²]

3. 具有两个不同不可约表示的字符作为分量的向量是正交的。

Σ_R [X_iR * X_jR] = 0，如果 i =/= j

4. 在给定的表示（可约或不可约）中，属于同一类对称算子的所有矩阵的字符相同。

类直接对应于等效运算的集合。当一个运算可以通过对称运算可达的新坐标系替换另一个运算时，两个运算属于同一类。例如，C₇ 点群将具有 C₇¹、C₇²、C₇³、C₇⁴、C₇⁵、C₇⁶、C₇⁷。由于 cos(θ) = cos(θ)，因此与这些矩阵相关的字符相同。在这种情况下，C₇¹=C₇⁶、C₇² = C₇⁵、C₇³ = C₇⁴，以及 C₇⁷ = E，因为它们属于同一类。我们可以将 C₇ 点群的对称性简化为 2 C₇¹、2C₇²、2C₇³ 和 E，因为有两项操作属于同一类。

5. 群的不可约表示的数量等于群中类的数量。

图 5. a) 蓝色阴影部分：不可约表示 b) 绿色阴影部分：可约表示 c) 黄色阴影部分：将可约表示简化为不可约表示

图 5 中绿色阴影部分是根据对称运算后未移动的分子数量找到的可约表示。例如，如果我们从图 5 中查看 C_2v 对称分子（例如水）的 Γ_σ，我们将关注对称运算后未移动的 σ 键的数量。在水分子中，有两个 s 键，即两个 O-H 键。如果我们应用 E，两个键都不会移动，因此可约表示将为 2，因为每个未移动的 σ 键贡献 1 个可约表示。如果我们对其应用 C₂ 操作，这两个键都会移动，其中 O-H 键会交换位置。这意味着没有未移动的 σ 键，因此可约表示将为零，如图 5 b 所示。

图 5 中黄色阴影部分是将可约表示简化为不可约表示。这可以通过使用公式来完成，n_i = ${1 \over h}$ΣNX_RX_I，其中 n_i = 不可约表示在可约表示中出现的次数，N = 每个对称元素符号前面的系数（显示在字符表的顶行），h = 群的阶（系数 N 的总和），X_R、X_I = 可约表示和不可约表示的字符。

引用

1.     Pfennig, Brian (2015). 无机化学原理. 新泽西州霍博肯：John Wiley & Sons, Inc.. pp. 195–202. ISBN 978-1-118-85910-0.