所有正常的物质体,如固体和气体,都服从质量连续性方程。在直角坐标系中,可以使用多种符号方法表示它。
∂ ρ ∂ t + ∂ ( ρ u i ) ∂ x i = ∂ ρ ∂ t + ∇ ∙ ρ V = ∂ ρ ∂ t + ∂ ( ρ u x ) ∂ x + ∂ ( ρ u y ) ∂ y + ∂ ( ρ u z ) ∂ z = 0 {\displaystyle {\frac {\partial \rho }{\partial t}}+{\frac {\partial (\rho {{u}_{i}})}{\partial {{x}_{i}}}}={\frac {\partial \rho }{\partial t}}+\nabla \bullet \rho V={\frac {\partial \rho }{\partial t}}+{\frac {\partial (\rho {{u}_{x}})}{\partial x}}+{\frac {\partial (\rho {{u}_{y}})}{\partial y}}+{\frac {\partial (\rho {{u}_{z}})}{\partial z}}=0}
本质上,方程的右侧解释了小体积内的质量流入/流出率。如果总和为零,则密度不会随时间变化。该物质被认为是不可压缩的 ,信号传播速度是无限的。任何局部动作都会立即传递到所有其他位置。所有材料都具有一定程度的可压缩性 ,因此密度会随时间变化,并且具有有限的传播速度。任何局部动作都需要一定的时间才能到达远程位置,因此所有描述性方程都必须包含一个时间延迟因子。由于这里关注的是航空声学,因此传播速度由与气体特性相关的几个因素决定。气体的运动受上述方程以及动量方程的控制,该方程将流体响应与几种力联系起来;该方程是非线性的。
∂ ( ρ u i ) ∂ t + ∂ ( ρ u i u j ) ∂ x j = ∂ p ∂ x j + υ ∂ u i ∂ x j {\displaystyle {\begin{aligned}&{\frac {\partial (\rho {{u}_{i}})}{\partial t}}+{\frac {\partial (\rho {{u}_{i}}{{u}_{j}})}{\partial {{x}_{j}}}}={\frac {\partial p}{\partial {{x}_{j}}}}+\upsilon {\frac {\partial {{u}_{i}}}{\partial {{x}_{j}}}}\\&\\\end{aligned}}}
如果做出一些简化的假设,则可以从中提取线性声波方程。
∂ 2 s ∂ x 2 − 1 c 0 2 ∂ 2 s ∂ t 2 = 0 s = ρ − ρ 0 ρ 0 {\displaystyle {\begin{aligned}&{\frac {{{\partial }^{2}}s}{\partial {{x}^{2}}}}-{\frac {1}{c_{0}^{2}}}{\frac {{{\partial }^{2}}s}{\partial {{t}^{2}}}}=0\\&s={\frac {\rho -{{\rho }_{0}}}{{\rho }_{0}}}\\\end{aligned}}}
这里用密度变化来表示,并与一个恒定的流体密度和一个恒定的传播速度(称为声速)相关联;这些用下标 0 表示。该速度基于所有物理变化都很小。如果不是这样,传播速度会更高,并导致众所周知的冲击波现象。这里的发展将通过一个边界将区域隔开,在这个边界之外,波动方程适用。这个方程用于波动传播,不包含源项。Lighthill 的开创性工作 [ 1] T i j {\displaystyle {{T}_{ij}}}
∂ 2 ρ ∂ t 2 − c 0 2 ∂ 2 ρ ∂ x i 2 = ∂ 2 T i j ∂ x i ∂ x j T i j = ρ u i u j − σ i j + ( p − c 0 2 ρ ) δ i j {\displaystyle {\begin{aligned}&{\frac {{{\partial }^{2}}\rho }{\partial {{t}^{2}}}}-c_{0}^{2}{\frac {{{\partial }^{2}}\rho }{\partial x_{i}^{2}}}={\frac {{{\partial }^{2}}{{T}_{ij}}}{\partial {{x}_{i}}\partial {{x}_{j}}}}\\&{{T}_{ij}}=\rho {{u}_{i}}{{u}_{j}}-{{\sigma }_{ij}}+(p-c_{0}^{2}\rho ){{\delta }_{ij}}\\\end{aligned}}}
有许多文章展示了该方程的一般解 气动声学 [ 2] [ 3] [ 4]
c 0 2 ( ρ − ρ 0 ) = ∂ 2 ∂ x i x j ∫ V [ T i j ] d 3 y 4 π r − ∂ ∂ x i ∮ S [ ρ u i u j + p i j ′ ] d S j ( y ) 4 π r + ∂ ∂ t ∮ S [ ρ u j ] d S j ( y ) 4 π r {\displaystyle c_{0}^{2}(\rho -{{\rho }_{0}})={\frac {{\partial }^{2}}{\partial {{x}_{i}}{{x}_{j}}}}\int \limits _{V}{\left[{{T}_{ij}}\right]}{\frac {{{d}^{3}}y}{4\pi r}}-{\frac {\partial }{\partial {{x}_{i}}}}\oint \limits _{S}{\left[\rho {{u}_{i}}{{u}_{j}}+p_{ij}^{'}\right]{\frac {d{{S}_{j}}(y)}{4\pi r}}}+{\frac {\partial }{\partial t}}\oint \limits _{S}{\left[\rho {{u}_{j}}\right]{\frac {d{{S}_{j}}(y)}{4\pi r}}}}
变量 r 是声源区域 y 到远场位置 x 的距离。方括号表示与该位置相关的时间延迟因子。第一项指的是整个应力张量 T i j {\displaystyle {{T}_{ij}}} ϕ {\displaystyle \phi }
假设我们在点 x 0 {\displaystyle \mathbf {x} _{0}}
1 c 0 2 ∂ 2 ϕ ∂ t 2 − ∇ 2 ϕ = − q ( t ) δ ( x − x 0 ) {\displaystyle {\frac {1}{c_{0}^{2}}}{\frac {\partial ^{2}\phi }{\partial \,t^{2}}}-\nabla ^{2}\phi =-q(t)\delta (\mathbf {x-x_{0}} )}
使用之前介绍的自由空间格林函数 [1] ,速度势将为
ϕ ( x , t ) = 1 4 π ∫ − ∞ ∞ q ( y , t − | x − y | / c 0 ) δ ( y − x 0 ) | x − y | d 3 y d τ = − q ( t − | x − x 0 | / c 0 ) 4 π | x − x 0 | {\displaystyle \phi (x,t)={\frac {1}{4\pi }}\int _{-\infty }^{\infty }{\frac {q(\mathbf {y} ,t-|\mathbf {x} -\mathbf {y} |/c_{0})\delta (\mathbf {y-x_{0}} )}{|\mathbf {x} -\mathbf {y} |}}d^{3}\,\mathbf {y} d\tau =-{\frac {q(t-|\mathbf {x-x_{0}} |/c_{0})}{4\pi \,|\mathbf {x-x_{0}} |}}}
如果声源位于原点,则上述解看起来像下面的图片。正如你所看到的,这种类型的声源产生对称的球面波。这种全方向声源被称为 **单极子**。
上述一般理论包含一个描述导致声场的运动的源项。它可以是单个声源,也可以是具有已知特性的声源分布(利希特)。下面,声源被视为黑盒子,被封闭在一个球形边界内,在这个边界之外声波方程是有效的。由此,从声学介质中的运动推导出声源的性质。在这种特定情况下,我们只关心与单个单极子声源相关的球面对称声学运动。这个波动方程可以用以下形式描述
∂ ∂ r 2 ( r ϕ ) − 1 c 0 2 ∂ ∂ t 2 ( r ϕ ) = 0 ϕ ( r , t ) = Q 4 π r F ( t − r c 0 ) p ( r , t ) = ρ 0 ∂ ϕ ∂ t {\displaystyle {\begin{aligned}&{\frac {\partial }{\partial {{r}^{2}}}}\left(r\phi \right)-{\frac {1}{c_{0}^{2}}}{\frac {\partial }{\partial {{t}^{2}}}}\left(r\phi \right)=0\\&\phi \left(r,t\right)={\frac {Q}{4\pi r}}F\left(t-{\frac {r}{{c}_{0}}}\right)\\&p\left(r,t\right)={{\rho }_{0}}{\frac {\partial \phi }{\partial t}}\\&\\\end{aligned}}}
符号 φ 被称为速度势 ,从中可以推导出大多数物理变量,例如压力或速度。字母 F 代表任意函数。对维度的分析表明 Q 的维度是 L 3 / T {\displaystyle {{L}^{3}}/T} W 可以用基本的方式表示为
W = 1 4 π Z 0 ( ∂ M ∂ t ) 2 ¯ {\displaystyle W={\frac {1}{4\pi {{Z}_{0}}}}{\overline {{\left({\frac {\partial M}{\partial t}}\right)}^{2}}}}
Z0 是声波传播介质的特征阻抗 。单极子的声功率可以解释为质量流量率 M 随时间变化率的均方 。这种关系适用于任何波动流量,无论随机还是周期性。最感兴趣的是以规定频率的周期性运动。它由弧度频率 ω=2πf 描述,其中 f 是以赫兹为单位的频率。通常会为点 单极子推导出关系式,但如果忽略源函数,则当接近源点时,解会发散。如果描述了具有有限半径 a 的单极子(脉动球体),这并不是一个障碍。此情况下,两个有用的关系是
u ( a , t ) = u a e i ω t Q = 4 π a 2 u a e i ω t {\displaystyle {\begin{array}{*{35}{l}}u\left(a,t\right)={{u}_{a}}{{e}^{i\omega t}}&{}\\Q=4\pi {{a}^{2}}{{u}_{a}}{{e}^{i\omega t}}&{}\\\end{array}}}
其中 a 代表球体半径,ua 代表表面上的径向速度。声压的波动方程解可以表示为
p ( r , t ) = [ 1 1 + i k a ] ( a r ) Z 0 u a e i ( ω t − k ( r − a ) ) k = ω c 0 = 2 π f c 0 = 2 π λ {\displaystyle {\begin{aligned}&p\left(r,t\right)=\left[{\frac {1}{1+ika}}\right]\left({\frac {a}{r}}\right){{Z}_{0}}{{u}_{a}}{{e}^{i\left(\omega t-k\left(r-a\right)\right)}}\\&k={\frac {\omega }{{c}_{0}}}={\frac {2\pi f}{{c}_{0}}}={\frac {2\pi }{\lambda }}\\\end{aligned}}}
单极子辐射阻抗 符号k 被称为波数 ,尽管它具有倒数长度的量纲。当它与距离(如r )结合时,它被解释为用波长表示的距离。方括号中的压力项包含一个复数变量。这是由于两种运动:反应运动和阻尼运动。反应运动可以认为是不可压缩的;压力与速度正交,因此对介质不做功。阻尼运动代表对介质做功并向源辐射能量的压缩运动。大多数声音测量都是在距离声源足够远的距离处进行的,因此只测量阻尼压力或声压。该距离称为远场 ,而反应运动占主导的距离称为近场 。这两个场之间的边界随着声源强度的增加而增加,随着频率的增加而减小。压力方程中方括号中的项由两个部分组成,即单极子看到的阻尼R 和反应X 辐射阻抗 。下面的两个方程式是它们的表达式。右侧的图形显示了两种阻抗随无量纲频率的变化。在波长非常接近声源(低频)的情况下,大部分运动都是不可压缩的,只有很少一部分输入能量作为声音辐射出去。扬声器设计者在这些频率下提高声源强度,以使整体频率响应平坦。在较高频率下,单极子非常有效地辐射声音。对于单个频率的有限单极子,声功率可以用简单的方式表示
A 是半径为a 的球体的表面积,R 是球体表面上的阻尼辐射阻抗。
单极子方向性 当单极子位于硬反射平面之上距离为h的地方时,会在表面下方相同的距离处出现一个镜像源。声功率表达式必须考虑与反射相关的时延。该方程为
W = 2 A u a 2 R [ 1 + sin ( 2 k h ) 2 k h ] {\displaystyle W=2Au_{a}^{2}R\left[1+{\frac {\sin(2kh)}{2kh}}\right]}
附加项解释了相长/相消干涉效应。当距离表面接近零时,声功率将增加4倍(6 dB)。右侧的图形展示了干涉效应的一个例子;该图形显示了平面之上右象限中的声压级。一个单极子位于硬反射表面上方 10 英寸处,以 500 Hz 的频率辐射。相消干涉发生在距原点约 45 度的地方。蓝色弧线代表均匀单极场。在更一般的情况下,有两个单极子彼此靠近。第二个声源的输出和相位可能与第一个声源不同。一个有趣的情况是,每个声源的尺寸和频率都相同。对于这种情况,声功率方程变为
W = A u 1 2 R [ 1 + ( u 2 2 u 1 2 ) + 2 u 2 u 1 sin ( 2 k h ) 2 k h cos δ ] {\displaystyle W=Au_{1}^{2}R\left[1+\left({\frac {u_{2}^{2}}{u_{1}^{2}}}\right)+{\frac {2{{u}_{2}}}{{u}_{1}}}{\frac {\sin(2kh)}{2kh}}\cos \delta \right]}
单极子干涉 燃烧单极子 脉冲喷气发动机噪声 符号u1 和 u2 代表两个声源的表面速度,字母 δ 代表两者之间的相位差。右图显示了两个单极子在 1000 Hz 频率下辐射,相距 72 厘米,相位差为 180 度的组合声压级的示例。请注意,由于相位相反,它们之间平面的声级被最小化。
现实世界中很少有声源能很好地近似于理论上的单极子。一个例子是迄今为止存在过的最大的单极子。它是在苏联新地岛上引爆的 5700 万吨氢弹。 [ 5] 单极子类 。与理论单极子的相似之处在于,有一个可变质量流量产生声场。不同之处在于,固体边界是声源的组成部分,而不是仅仅在附近。一个例子是平面表面上的活塞;该理论已被研究出来。 [ 6] [ 7]
还有一类单极子类声源被称为气动哨声。 [ 8]
比较同一类型声源的不同操作模式和尺寸时,几何相似性和动态相似性非常重要。几何形状由尺寸L 描述,动力学由速度U 描述。如果正确选择这些值,它们将成为设备的特征。它们可用于确定如果设备的尺寸或速度发生变化,声音功率的变化。下面的第一个方程是点单极子在离散频率下的方程。体积流量项可以用无量纲版本替换,频率可以用无量纲斯特罗哈尔数替换。该数字是在研究圆柱体上的涡流脱落时由文森茨·斯特罗哈尔提出的。他发现它在一定范围内流速(接近 0.2)是相对恒定的。斯特罗哈尔数现在可以通过使质量连续性方程无量纲直接推导出来。如果将这两个无量纲值代入声音功率方程,则得到最后一个方程。对于许多声源来说,这两个无量纲参数都相对恒定,因此声音功率随着特征速度的四次方和特征长度的二次方而增加。 [ 9]
汽车声级 W = k 2 Z 0 Q 2 4 π Q ^ = Q U L 2 S = f L U W = π ρ 0 c 0 Q ^ 2 S 2 U 4 L 2 {\displaystyle {\begin{aligned}&W={\frac {{{k}^{2}}{{Z}_{0}}{{Q}^{2}}}{4\pi }}\\&{\widehat {Q}}={\frac {Q}{U{{L}^{2}}}}\\&S={\frac {fL}{U}}\\&W={\frac {\pi {{\rho }_{0}}}{{c}_{0}}}{{\widehat {Q}}^{2}}{{S}^{2}}{{U}^{4}}{{L}^{2}}\\\end{aligned}}}
汽车声谱 后一个方程适用性的一个很好的例子是机动车声音。右侧的上面图显示了从各种汽车在几个速度下在 50 英尺处测量的声压级。[ 10] U 4 {\displaystyle {{U}^{4}}} [ 11]
偶极子是波浪方程中出现的一个声源,表示为
1 c 0 2 ∂ 2 p ∂ t 2 − ∇ 2 p = ∂ ∂ x j ( f j ( t ) δ ( x − x 0 ) ) {\displaystyle {\frac {1}{c_{0}^{2}}}{\frac {\partial ^{2}p}{\partial \,t^{2}}}-\nabla ^{2}p={\frac {\partial }{\partial x_{j}}}\left(f_{j}(t)\delta (\mathbf {x-x_{0}} )\right)}
与单极子不同,偶极子方程有两个方向,一个是来自声源的半径,另一个是角度。声源外部的声学运动方程可以用这些坐标表示为
1 r 2 ∂ ∂ r ( r 2 ∂ ϕ ∂ r ) + 1 r 2 sin θ ∂ ∂ θ ( sin θ ∂ ϕ ∂ θ ) − 1 c 0 2 ∂ 2 ϕ ∂ t 2 = 0 p ( r , θ , t ) = ρ 0 ∂ ϕ ∂ t u r ( r , θ , t ) = − ∂ ϕ ∂ r u θ ( r , θ , t ) = − 1 r ∂ ϕ ∂ θ {\displaystyle {\begin{aligned}&{\frac {1}{{r}^{2}}}{\frac {\partial }{\partial r}}\left({{r}^{2}}{\frac {\partial \phi }{\partial r}}\right)+{\frac {1}{r^{2}\sin \theta }}{\frac {\partial }{\partial \theta }}\left(\sin \theta {\frac {\partial \phi }{\partial \theta }}\right)-{\frac {1}{c_{0}^{2}}}{\frac {\partial ^{2}\phi }{\partial {{t}^{2}}}}=0\\&p\left(r,\theta ,t\right)={{\rho }_{0}}{\frac {\partial \phi }{\partial t}}\\&{{u}_{r}}\left(r,\theta ,t\right)=-{\frac {\partial \phi }{\partial r}}\\&{{u}_{\theta }}\left(r,\theta ,t\right)=-{\frac {1}{r}}{\frac {\partial \phi }{\partial \theta }}\\\end{aligned}}}
波动方程的外向解是
ϕ ( r , θ , t ) = Q 4 π 1 + i k r r 2 cos θ e i ( ω t − k r ) {\displaystyle \phi \left(r,\theta ,t\right)={\frac {Q}{4\pi }}{\frac {1+ikr}{{r}^{2}}}\cos \theta {{e}^{i\left(\omega t-kr\right)}}}
这个结果可以通过在特定方向上对单极子速度势进行微分得到。
ϕ ( r , θ , t ) = ∂ ∂ r ( Q m 4 π r e i ( ω t − k r ) ) ∗ ∂ r ∂ z = Q d 4 π 1 + i k r r 2 cos θ e i ( ω t − k r ) {\displaystyle \phi (r,\theta ,t)={\frac {\partial }{\partial r}}\left({\frac {{Q}_{m}}{4\pi r}}{{e}^{i(\omega t-kr)}}\right)*{\frac {\partial r}{\partial z}}={\frac {{Q}_{d}}{4\pi }}{\frac {1+ikr}{{r}^{2}}}\cos \theta {{e}^{i(\omega t-kr)}}}
从某种意义上说,偶极子是两个在特定方向上对齐的合并单极子。在这种情况下,Q 的维数是 L 4 ╱ T {\displaystyle {}^{{L}^{4}}\!\!\diagup \!\!{}_{T}\;} F 与 Q 变量的关系为 Q = i 3 F z k Z 0 {\displaystyle Q={\frac {i3{{F}_{z}}}{k{{Z}_{0}}}}}
ϕ ( r , θ , t ) = 3 F z 4 π k Z 0 [ 1 + i k r r 2 ] cos θ e i ( ω t − k r ) {\displaystyle \phi (r,\theta ,t)={\frac {3{{F}_{z}}}{4\pi k{{Z}_{0}}}}\left[{\frac {1+ikr}{{r}^{2}}}\right]\cos \theta {{e}^{i(\omega t-kr)}}}
与单极子发展类似,偶极子的声功率可以用一种基本的方式用施加的力来表示,如下所示
W = 3 4 π Z 0 c 0 2 ( ∂ F z ∂ t ) 2 ¯ {\displaystyle W={\frac {3}{4\pi {{Z}_{0}}c_{0}^{2}}}{\overline {{\left({\frac {\partial {{F}_{z}}}{\partial t}}\right)}^{2}}}}
声功率可以解释为施加在介质上特定方向上的力的变化率的均方 。
最感兴趣的是半径为 a 的刚性球体,它在 z 方向上以特定频率振动(有限尺寸的偶极子)。各种场是
p ( r , θ , t ) = i 3 F z 4 π r 2 ( 1 + i k r 1 + i k a ) c o s θ e i ( ω t − k ( r − a ) ) u r ( r , θ , t ) = 3 F z 4 π k r 3 Z 0 ( 2 ( 1 + i k r ) − k 2 r 2 1 + i k a ) c o s θ e i ( ω t − k ( r − a ) ) u θ ( r , θ , t ) = − i 3 F z 4 π k r 3 Z 0 ( 1 + i k r 1 + i k a ) s i n θ e i ( ω t − k ( r − a ) ) {\displaystyle {\begin{aligned}&p\left(r,\theta ,t\right)={\frac {i3{{F}_{z}}}{4\pi {{r}^{2}}}}\left({\frac {1+ikr}{1+ika}}\right)cos\theta {{e}^{i(\omega t-k(r-a))}}\\&{{u}_{r}}\left(r,\theta ,t\right)={\frac {3{{F}_{z}}}{4\pi k{{r}^{3}}{{Z}_{0}}}}\left({\frac {2(1+ikr)-{{k}^{2}}{{r}^{2}}}{1+ika}}\right)cos\theta {{e}^{i(\omega t-k(r-a))}}\\&{{u}_{\theta }}\left(r,\theta ,t\right)={\frac {-i3{{F}_{z}}}{4\pi k{{r}^{3}}{{Z}_{0}}}}\left({\frac {1+ikr}{1+ika}}\right)sin\theta {{e}^{i(\omega t-k(r-a))}}\\\end{aligned}}}
强度有两个分量。径向强度具有阻性和感抗分量,而角向强度仅具有感抗分量。这表明该运动在声场中存储的不可压缩能量比单极子更多。右侧的图形显示了由此产生的指向性图。
偶极子强度场 I r ( r , θ ) = 9 F z 2 16 π 2 Z 0 [ k 2 r 2 r 4 ( 1 + k 2 a 2 ) = + i 2 + k 2 r 2 r 4 ( 1 + k 2 a 2 ) k r ] c o s 2 θ I θ ( r , θ ) = i 9 F z 2 32 π 2 Z 0 [ 1 + k 2 r 2 r 4 ( 1 + k 2 a 2 ) k r ] s i n 2 θ {\displaystyle {\begin{aligned}&{{I}_{r}}(r,\theta )={\frac {9F_{z}^{2}}{16{{\pi }^{2}}{{Z}_{0}}}}\left[{\frac {{{k}^{2}}{{r}^{2}}}{{{r}^{4}}(1+{{k}^{2}}{{a}^{2}})}}=+i{\frac {2+{{k}^{2}}{{r}^{2}}}{{{r}^{4}}(1+{{k}^{2}}{{a}^{2}})kr}}\right]co{{s}^{2}}\theta \\&{{I}_{\theta }}(r,\theta )={\frac {i9F_{z}^{2}}{32{{\pi }^{2}}{{Z}_{0}}}}\left[{\frac {1+{{k}^{2}}{{r}^{2}}}{{{r}^{4}}(1+{{k}^{2}}{{a}^{2}})kr}}\right]sin2\theta \\\end{aligned}}}
有限偶极子的声功率为
W = 3 F z 2 4 π a 2 Z 0 [ k 2 a 2 1 + k 2 a 2 ] {\displaystyle W={\frac {3F_{z}^{2}}{4\pi {{a}^{2}}{{Z}_{0}}}}\left[{\frac {{{k}^{2}}{{a}^{2}}}{1+{{k}^{2}}{{a}^{2}}}}\right]}
有限偶极子的辐射阻抗为
偶极子阻抗 R = Z 0 k 4 a 4 4 + k 4 a 4 X = Z 0 k a ( 2 + k 2 a 2 ) 4 + k 4 a 4 {\displaystyle {\begin{aligned}&R={{Z}_{0}}{\frac {{{k}^{4}}{{a}^{4}}}{4+{{k}^{4}}{{a}^{4}}}}\\&X={{Z}_{0}}{\frac {ka(2+{{k}^{2}}{{a}^{2}})}{4+{{k}^{4}}{{a}^{4}}}}\\\end{aligned}}}
偶极子在低频下的电抗明显高于单极子,表明不可压缩场中储存了大量能量。低频下的电阻阻抗远低于单极子,表明这些频率下的辐射效率低下。
当偶极子距离硬反射面h 时,镜像源出现在表面下方相同的距离。与单极子不同,力的方向矢量以及与反射相关的时延也必须考虑在内。均方声压方程为
p p ∗ = 9 F z 2 16 π 2 ( 1 + k 2 a 2 ) [ ( 1 + k 2 r 1 2 ) r 1 4 cos 2 α 1 + ( 1 + k 2 r 2 2 ) r 2 4 cos 2 α 2 + 2 cos α 1 cos α 2 r 1 2 r 2 2 [ ( 1 + k r 1 r 2 ) cos k ( r 2 − r 1 ) + k ( r 2 − r 1 ) sin k ( r 2 − r 1 ) ] ] {\displaystyle p{{p}^{*}}={\frac {9F_{z}^{2}}{16{{\pi }^{2}}(1+{{k}^{2}}{{a}^{2}})}}\left[{\frac {(1+{{k}^{2}}r_{1}^{2})}{r_{1}^{4}}}{{\cos }^{2}}{{\alpha }_{1}}+{\frac {(1+{{k}^{2}}r_{2}^{2})}{r_{2}^{4}}}{{\cos }^{2}}{{\alpha }_{2}}+{\frac {2\cos {{\alpha }_{1}}\cos {{\alpha }_{2}}}{r_{1}^{2}r_{2}^{2}}}\left[(1+k{{r}_{1}}{{r}_{2}})\cos k({{r}_{2}}-{{r}_{1}})+k({{r}_{2}}-{{r}_{1}})\sin k({{r}_{2}}-{{r}_{1}})\right]\right]}
垂直偶极子方向性 水平偶极子方向性 由于反射力矢量方向是源矢量的镜像,因此需要考虑两个角度。图中给出了这个繁琐方程的影响示例。在第一个示例中,左侧,偶极子相对于水平表面垂直定向,并在 1000 Hz 频率下辐射。源位于表面上方 20 厘米,因此会发生相消干涉,标准偶极子方向性会发生改变。第二个图,右侧,是偶极子轴处于水平状态时的情况;其他条件保持不变。两个相互作用的偶极子在任意大小、频率、角度和相位差下更一般的情况可以被公式化,但不会更有启发性。
很少有声源接近于理论偶极子;大多数被称为类偶极子。相似之处在于产生的声场。不同之处在于产生声场的过程。在实际情况下,驱动声场的力是由流体与固体物体相互作用产生的动量波动产生的。虽然单极子源明显与密度变化相关,但在实际偶极子情况下,密度变化可能会被埋藏在一个可以被视为不可压缩的流场中,以便进行分析。涡声理论被发展出来来处理这种情况[ 12] [ 13] [ 14] [ 15]
两个单极子的偶极子 两个涡流 振荡球体 一个典型的涡流例子是气流经过圆柱体产生的风鸣声。涡流交替地从圆柱体中脱落。左图显示了从圆柱体(深色圆圈)中脱落的两个相干涡流的两个阶段。围绕圆柱体的振荡循环导致产生一个类偶极声场的力量。与理论偶极子不同,不对称性导致垂直于流动的升力偶极子和平行于流动的阻力偶极子。正是这种现象被文森佐·斯特鲁哈尔研究[ 16] [ 17] [ 18] 由于在自由流中,总涡流强度(循环乘以面积)不可能发生变化,因此没有净偶极子强度,但每个移动的涡量元素仍然会引起局部类偶极子流动。一个关键的结果是,在略微可压缩的流体中,涡量可以被认为是诱导整个流场,包括流体力学部分和声学部分。
风鸣声流 排气偶极子 来自环的偶极子声 当比较同一源类型不同操作模式和尺寸时,几何相似性和动态相似性很重要。几何形状由尺寸 L 描述,动力学由速度 U 描述。如果这些值选择得当,它们就会成为设备的特征。它们可以用来确定如果设备的尺寸或速度发生变化,声功率的变化。下面第一个方程是点偶极子在离散频率下的方程。波动力可以用无量纲版本代替,频率可以用无量纲斯特鲁哈尔数代替。如果将这些无量纲值代入声功率方程,则得到最后一个方程。对于许多偶极子声源,这两个无量纲参数都相对恒定,因此声功率随特征速度的六次方和特征长度的二次方而增加。这种关系已在许多实际声源中得到证实。
W = 3 k 2 F z 2 4 π Z 0 F z ^ = F z ρ 0 U 2 L 2 S = f L U W = 3 π ρ 0 c 0 3 F z ^ 2 S 2 U 6 L 2 {\displaystyle {\begin{aligned}&W={\frac {3{{k}^{2}}F_{z}^{2}}{4\pi {{Z}_{0}}}}\\&{\widehat {{F}_{z}}}={\frac {{F}_{z}}{{{\rho }_{0}}{{U}^{2}}{{L}^{2}}}}\\&S={\frac {fL}{U}}\\&W={\frac {3\pi {{\rho }_{0}}}{c_{0}^{3}}}{{\widehat {{F}_{z}}}^{2}}{{S}^{2}}{{U}^{6}}{{L}^{2}}\\\end{aligned}}}
后缘噪声 涡旋哨声是由管口处的旋流前移产生的[ 19] [ 20] [ 21] [ 22]
四极子是涉及两个空间导数的源分布。
1 c 0 2 ∂ 2 p ∂ t 2 − ∇ 2 p = ∂ 2 T i j ∂ x i ∂ x j {\displaystyle {\frac {1}{c_{0}^{2}}}{\frac {\partial ^{2}p}{\partial \,t^{2}}}-\nabla ^{2}p={\frac {\partial ^{2}T_{ij}}{\partial x_{i}\partial x_{j}}}}
下方显示了一个点横向四极子产生的声场。请注意最大声级的角度。
与偶极子和单极子不同,四极子的方程具有三个方向,即从源头的半径和两个角度。该方程可以用球坐标表示,其中线性方程有效,如
1 r 2 ∂ ∂ r ( r 2 ∂ ϕ ∂ r ) + 1 r 2 sin θ ∂ ∂ θ ( sin θ ∂ ϕ ∂ θ ) + 1 r 2 sin 2 θ ∂ 2 ϕ ∂ ψ − 1 c 0 2 ∂ ∂ r 2 ( r ϕ ) = 0 p ( r , θ , ψ , t ) = ρ 0 ∂ ϕ ∂ t u r ( r , θ , ψ , t ) = − ∂ ϕ ∂ r u θ ( r , θ , ψ , t ) = − 1 r ∂ ϕ ∂ θ u ψ ( r , θ , ψ , t ) = − 1 r sin θ ∂ ϕ ∂ ψ {\displaystyle {\begin{aligned}&{\frac {1}{{r}^{2}}}{\frac {\partial }{\partial r}}\left({{r}^{2}}{\frac {\partial \phi }{\partial r}}\right)+{\frac {1}{{{r}^{2}}\sin \theta }}{\frac {\partial }{\partial \theta }}\left(\sin \theta {\frac {\partial \phi }{\partial \theta }}\right)+{\frac {1}{{{r}^{2}}{{\sin }^{2}}\theta }}{\frac {{{\partial }^{2}}\phi }{\partial \psi }}-{\frac {1}{c_{0}^{2}}}{\frac {\partial }{\partial {{r}^{2}}}}\left(r\phi \right)=0\\&p\left(r,\theta ,\psi ,t\right)={{\rho }_{0}}{\frac {\partial \phi }{\partial t}}\\&{{u}_{r}}\left(r,\theta ,\psi ,t\right)=-{\frac {\partial \phi }{\partial r}}\\&{{u}_{\theta }}\left(r,\theta ,\psi ,t\right)=-{\frac {1}{r}}{\frac {\partial \phi }{\partial \theta }}\\&{{u}_{\psi }}\left(r,\theta ,\psi ,t\right)=-{\frac {1}{r\sin \theta }}{\frac {\partial \phi }{\partial \psi }}\\\end{aligned}}}
四极子声源 单极子是标量,偶极子是向量,而四极子是二阶张量。偶极子可以被视为两个相互异相的紧密单极子。四极子可以被视为两个紧密偶极子,它们的力矢量方向相反,或者四个单极子像右侧图中所示那样排列。横向四极子是力矢量平行于彼此,但相互横向的四极子。如该图所示,横向四极子与波动的剪切力有关。纵向四极子是力矢量彼此平行,但处于同一直线上的四极子。如该图所示,纵向四极子与拉伸力(泊松比型变形)有关。
这些可以被建模为四个单极子、两个偶极子或两个涡环。偶极子的力向量如上图所示,另外两个的流场如右侧图所示。没有 严格的径向流向量表明有效的声波产生。虽然没有显示出来,但四个四十五度角的斜流的径向分量是最大的(见上面的动画)。因此,可以推断出四个声波瓣,而无需借助数学。这种类型的四极子可以存在于具有速度梯度的流动中,特别是在湍流中。[ 23] [ 24]
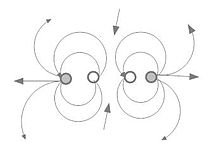
横向四极子近流场的流体力学可以通过多种方式进行建模。左侧的图使用四个单极子来创建流场。正是这种布置成为下一节第一个方程的基础。中间图使用两个偶极子(在这里显示为两个球体)来创建流场。也可以使用两个力向量。右侧图使用两个涡环来创建流场。横向四极子的分布存在于具有速度梯度的流动中,特别是在高速湍流中。
横向四极子的单极子模型 横向四极子的涡旋模型 横向四极子的偶极子模型 横向四极子是指力向量平行但相互并列,如右上角上图所示。与不太复杂的声源一样,这种四极子也被认为是由四个点单极子组成,每一对纵向相隔有限距离d ,两对横向相隔距离D 。下面的等式是根据这些项表示声压的表达式。[ 25] Q 是点单极子的源函数。
p ( r , θ , ψ , t ) = Q Z 0 k 4 π r ( 4 k 2 d D ) cos θ sin θ cos ψ e i ( ω t − k r ) {\displaystyle p(r,\theta ,\psi ,t)={\frac {QZ{}_{0}k}{4\pi r}}(4{{k}^{2}}dD)\cos \theta \sin \theta \cos \psi {{e}^{i(\omega t-kr)}}}
一种更具启发性的方法是使用导数法。由于偶极子速度势是作为单极子的导数得到的,因此横向四极子速度势可以通过偶极子势的导数得到。对于横向四极子,导数是在垂直于主偶极子轴方向的方向上取的。这种方法揭示了作用在体积上的剪切力。第一个方程式是速度势;第二个是声压;第三个是均方声压。横向四极子声源可以表示为作用在体积上的剪切力时间变化率的均方的时均值 。
这种四极子的指向性如右侧图所示。三维形式很像一个拉长的气球。
横向四极子的指向性 φ ( r , θ , ψ , t ) = 3 F 4 π k Z 0 [ k 2 r 2 − 2 ( 1 + i k r ) r 3 ] cos θ sin θ cos ψ e i ( ω t − k r ) p ( r , θ , ψ , t ) = i 3 F 4 π [ k 2 r 2 − 2 ( 1 + i k r ) r 3 ] cos θ sin θ cos ψ e i ( ω t − k r ) p 2 ¯ ( r , θ , ψ ) = 9 ( ∂ F ∂ t ) 2 ¯ 16 π 2 [ 4 + k 4 r 4 r 6 ] cos 2 θ sin 2 cos 2 ψ {\displaystyle {\begin{aligned}&\varphi (r,\theta ,\psi ,t)={\frac {3F}{4\pi k{{Z}_{0}}}}\left[{\frac {{{k}^{2}}{{r}^{2}}-2(1+ikr)}{{r}^{3}}}\right]\cos \theta \sin \theta \cos \psi {{e}^{i(\omega t-kr)}}\\&p(r,\theta ,\psi ,t)={\frac {i3F}{4\pi }}\left[{\frac {{{k}^{2}}{{r}^{2}}-2(1+ikr)}{{r}^{3}}}\right]\cos \theta \sin \theta \cos \psi {{e}^{i(\omega t-kr)}}\\&{\overline {{p}^{2}}}(r,\theta ,\psi )={\frac {9{\overline {{\left({\frac {\partial F}{\partial t}}\right)}^{2}}}}{16{{\pi }^{2}}}}\left[{\frac {4+{{k}^{4}}{{r}^{4}}}{{r}^{6}}}\right]{{\cos }^{2}}\theta {{\sin }^{2}}{{\cos }^{2}}\psi \\\end{aligned}}}
其中时间导数表示作用在介质上的时变应力。
就像对单极子和偶极子所做的那样,几何和动态相似性可以通过使用特征尺寸 **L** 和特征速度 **U** 应用于四极子。下面的第一个方程使用波动应力 **τ** 的简化形式(尺寸 F/L),用于离散频率的点四极子。应力项可以用无量纲形式替换,频率项可以用斯特劳哈尔数替换。如果将这些无量纲值插入声功率方程,则得到下面的方程。这是众所周知的归因于莱特希尔的速率定律。由于斯特劳哈尔数被提升到高次幂,因此如果总体速度依赖性偏离该定律,也不要感到惊讶。
W = k 4 τ 2 120 π Z 0 τ ^ = τ ρ 0 U 2 L 3 S = f L U W = 2 π 3 ρ 0 15 c 0 5 S 4 τ ^ 2 U 8 L 2 {\displaystyle {\begin{aligned}&W={\frac {{{k}^{4}}{{\tau }^{2}}}{120\pi {{Z}_{0}}}}\\&{\widehat {\tau }}={\frac {\tau }{{{\rho }_{0}}{{U}^{2}}{{L}^{3}}}}\\&S={\frac {fL}{U}}\\&W={\frac {2{{\pi }^{3}}{{\rho }_{0}}}{15c_{0}^{5}}}{{S}^{4}}{{\widehat {\tau }}^{2}}{{U}^{8}}{{L}^{2}}\\\end{aligned}}}
辐射阻抗已经计算为[ 26]
横向四极子阻抗 R = Z 0 k 6 r 6 81 + 9 k 2 r 2 − 2 k 4 r 4 + k 6 r 6 X = Z 0 k r ( 27 + 6 k 2 r 2 + k 4 r 4 ) 81 + 9 k 2 r 2 − 2 k 4 r 4 + k 6 r 6 {\displaystyle {\begin{aligned}&R={{Z}_{0}}{\frac {{{k}^{6}}{{r}^{6}}}{81+9{{k}^{2}}{{r}^{2}}-2{{k}^{4}}{{r}^{4}}+{{k}^{6}}{{r}^{6}}}}\\&X={{Z}_{0}}{\frac {kr(27+6{{k}^{2}}{{r}^{2}}+{{k}^{4}}{{r}^{4}})}{81+9{{k}^{2}}{{r}^{2}}-2{{k}^{4}}{{r}^{4}}+{{k}^{6}}{{r}^{6}}}}\\\end{aligned}}}
右边的图显示了这些阻抗的图形表示。很明显,低频下的电阻辐射效率 **R** 比单极子和偶极子要差得多,而电抗 **X** 则大几个数量级。这些频率下的流动主要是不可压缩的。这表明四极子声辐射在高频和高剪切应力(高速流动)下更有效。
理论模型的轴线在定义的方向上,因此人们期望能够测量源的方向性。不幸的是,没有多少高阶源具有这种固定的方向性。人们最初对这些源的兴趣在于喷气发动机的噪声,这些噪声被确定为四极子性质。[ 27] [ 28]
同样,这些可以建模为四个单极子,两个偶极子或两个涡环。偶极子的力矢量如上图所示,另外两个的流场如右图所示。在这种情况下,存在纯径向流动矢量,表明在流动轴线上有效地产生声音。
纵向四极子的近场流场的流体力学可以用几种方法来建模。左边的图使用四个单极子来创建流场。正是这种布置成为下一节第一个方程的基础。中间的图使用两个偶极子(这里用两个球体表示)来创建流场。也可以使用两个力矢量。右边的图使用两个涡环来创建流场。这些模型表明体积的拉伸。
纵向四极子的单极子模型 纵向四极子的涡旋模型 纵向四极子的偶极子模型 纵向四极子是指力矢量平行且呈直线排列,如右上角的下方图形所示。与较简单的声源一样,该四极子被视为四个点单极子的集合,每对单极子在纵向方向上相隔有限距离d ,两对单极子在纵向方向上相隔距离D 。以下公式是声压的表达式,其中Q 为点单极子的源函数。[ 29]
p ( r , θ , t ) = Q Z 0 k 4 π r ( 4 k 2 d D ) cos 2 θ e i ( ω t − k r ) {\displaystyle p(r,\theta ,t)={\frac {QZ{}_{0}k}{4\pi r}}(4{{k}^{2}}dD){{\cos }^{2}}\theta {{e}^{i(\omega t-kr)}}}
更直观的方法是使用导数法。由于偶极子的速度势是通过单极子的导数获得的,因此纵向四极子的速度势可以通过偶极子速度势的导数获得。对于纵向四极子,导数是在与主偶极子轴相同的方向上取的。这种方法揭示了作用在体积上的拉伸力。第一个公式是速度势;第二个是声压;第三个是平均平方声压。纵向四极声源可以表示为作用在体积上的拉伸力的变化率的时间平均平方 。
这种四极子的指向性如右侧图所示。三维形式很像一个拉长的气球。
纵向四极子的指向性 φ ( r , θ , t ) = 3 F 4 π k Z 0 [ k 2 r 2 − 2 ( 1 + i k r ) r 3 ] cos 2 θ e i ( ω t − k r ) p ( r , θ , t ) = i 3 F 4 π [ k 2 r 2 − 2 ( 1 + i k r ) r 3 ] cos 2 θ e i ( ω t − k r ) p 2 ¯ ( r , θ ) = 9 ( ∂ F ∂ t ) 2 ¯ 16 π 2 [ 4 + k 4 r 4 r 6 ] cos 4 θ {\displaystyle {\begin{aligned}&\varphi (r,\theta ,t)={\frac {3F}{4\pi k{{Z}_{0}}}}\left[{\frac {{{k}^{2}}{{r}^{2}}-2(1+ikr)}{{r}^{3}}}\right]{{\cos }^{2}}\theta {{e}^{i(\omega t-kr)}}\\&p(r,\theta ,t)={\frac {i3F}{4\pi }}\left[{\frac {{{k}^{2}}{{r}^{2}}-2(1+ikr)}{{r}^{3}}}\right]{{\cos }^{2}}\theta {{e}^{i(\omega t-kr)}}\\&{\overline {{p}^{2}}}(r,\theta )={\frac {9{\overline {{\left({\frac {\partial F}{\partial t}}\right)}^{2}}}}{16{{\pi }^{2}}}}\left[{\frac {4+{{k}^{4}}{{r}^{4}}}{{r}^{6}}}\right]{{\cos }^{4}}\theta \\\end{aligned}}}
其中时间导数表示作用在介质上的时变应力。
与横向四极子类似,必须选择特征尺寸L 和特征速度U 。以下声功率方程式使用点纵向四极子在离散频率下的波动应力τ (尺寸为F/L)的简化表达式。同样,应力项可以被无量纲版本替换,频率项被斯特劳哈尔数替换。下面的公式类似于横向四极子的公式。
W = k 4 τ 2 40 π Z 0 τ ^ = τ ρ 0 U 2 L 3 S = f L U W = 2 π 3 ρ 0 5 c 0 5 S 4 τ ^ 2 U 8 L 2 {\displaystyle {\begin{aligned}&W={\frac {{{k}^{4}}{{\tau }^{2}}}{40\pi {{Z}_{0}}}}\\&{\widehat {\tau }}={\frac {\tau }{{{\rho }_{0}}{{U}^{2}}{{L}^{3}}}}\\&S={\frac {fL}{U}}\\&W={\frac {2{{\pi }^{3}}{{\rho }_{0}}}{5c_{0}^{5}}}{{S}^{4}}{{\widehat {\tau }}^{2}}{{U}^{8}}{{L}^{2}}\\\end{aligned}}}
一个纵向四极子类声场的示范是音叉。[30]
↑ Lighthill, M., "On sound Generated Aerodynamically. Part I: General Theory", Proc. Royal Soc. London, 1952 ↑ http://jullio.pe.kr/fluent6.1/help/html/acoustics/node4.htm ↑ Dawkins, S. "Aguide to Aeroacoustics", Bibliobazaar, 2011 ↑ Norton, M. Karczub, D. "Fundamentals of Noise and Vibration Analysis for Engineers" Cambridge University Press, 2003 ↑ http://gizmodo.com/5977824/the-biggest-bomb-in-the-history-of-the-world ↑ Kinlser, L.E., Frey, A.R., "fundamentals of Acoustics, John wiley and sons, 1962 ↑ Morse, P.M., Ingard, K.U. "Theoretical Acoustics", McGraw-Hill, 1968 ↑ https://sciam.cn/article/aerodynamic-whistles/ ↑ Lighthill, M., "On sound Generated Aerodynamically. Part I: General Theory", Proc. Royal Soc. London, 1952 ↑ Bernhard, R.J., Sandberg, U., "Where Does It Come From?", National Cooperative Highway Research Program, Report 630 ↑ http://ccrllc/files/Tools-for-Analyzing-Sound-Sources.pdf ↑ Powell, A. "Theory of Vortex Sound," Jo. Acoust. Soc. Am., 36, 177-194, 1964 ↑ Powell, A. "Vortex Sound: An alternative derivation of Mohring's formulation" Jo. Acoust. Soc. Am., 97, 684-686, 1995a ↑ Powell, A. "Vortex Sound Theory: Direct proof of equivalence of "vortex force" and "vorticity alone" formulations, n" Jo. Acoust. Soc. Am., 97, 1534-1537, 1995b ↑ Howe, M.S. "Vortex Sound", Cambridge University Press, 2003 ↑ Strouhal, V. "Ueber eine besondere Art der Tonerregung" (On an unusual sort of sound excitation), Annalen der Physik und Chemie, 3rd series, 5 (10) : 216–251, 1878 ↑ Phillips, O.M., "The intensity of Aeolian tones" Jo., Fluid Mech., 1, 607-624, 1956 ↑ Chanaud, R.C., Powell, A., "Some experiments concerning the hole and ring tone", Jo. Acoust. Soc. Am., 37, 5, 902-911, 1965 ↑ Vonnegut, B. "The Vortex Whistle" Jo. Acoust. Soc. Amer. 26, 16-20, 1952 ↑ Chanaud, R.C., "Experiments Concerning the Vortex Whistle", Jo. Acoust. Soc., Amer. 35, No. 7, 953-960, 1963 ↑ Powell, A., "On the Edge Tone", Jo. Acoust. Soc. Amer., 33, No. 4, 395-409, 1961 ↑ Hayden, R.E., Fox, H.L., Chanaud, R.C. "Some Factors Influencing Radiation from flow interaction with edges of finite Surfaces", NASA Cr-145073, 1976 ↑ Russell, D.A., Titlow, J.P., Bemmen,Y, "Acoustic monopoles, dipoles and quadrupoles:an experiment revisited", Am. J. Phys. 57, 8, August 1999 ↑ Dowling, A.P., ‘‘Steady-State Radiation From Sources,'’ Encyclopedia of Acoustics, . John Wiley and Sons, Chap. 9, 107–125, 1997. ↑ Russell, D.A., Titlow, J.P., Bemmen, Y, "Acoustic monopoles, dipoles and quadrupoles: An experiment revisited", Am. J. Phys. 57, 8, August 1999 ↑ Powell, A. Class Notes, UCLA, 1961 ↑ Lush, P.A., "Measurements of subsonic jet noise and comparison with theory", Jo. Fluid Mech. 46,3, 477-500, 1971 ↑ Goldstein, M. E., "A generalized acoustic analogy", Jo. Fluid Mech. 488, 315-333, 2003 ↑ Russell, D.A., Titlow, J.P., Bemmen, Y, "Acoustic monopoles, dipoles and quadrupoles: An experiment revisited", Am. J. Phys. 57, 8, August 1999 ↑ Russell, D.A., "On the sound field radiated by a tuning fork" Am. J. Phys. 68 ~121, December 2000 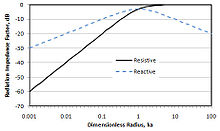
































![{\displaystyle c_{0}^{2}(\rho -{{\rho }_{0}})={\frac {{\partial }^{2}}{\partial {{x}_{i}}{{x}_{j}}}}\int \limits _{V}{\left[{{T}_{ij}}\right]}{\frac {{{d}^{3}}y}{4\pi r}}-{\frac {\partial }{\partial {{x}_{i}}}}\oint \limits _{S}{\left[\rho {{u}_{i}}{{u}_{j}}+p_{ij}^{'}\right]{\frac {d{{S}_{j}}(y)}{4\pi r}}}+{\frac {\partial }{\partial t}}\oint \limits _{S}{\left[\rho {{u}_{j}}\right]{\frac {d{{S}_{j}}(y)}{4\pi r}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9b75483b43dfda630514a935e11f85e64fa8b441)








![{\displaystyle {\begin{aligned}&p\left(r,t\right)=\left[{\frac {1}{1+ika}}\right]\left({\frac {a}{r}}\right){{Z}_{0}}{{u}_{a}}{{e}^{i\left(\omega t-k\left(r-a\right)\right)}}\\&k={\frac {\omega }{{c}_{0}}}={\frac {2\pi f}{{c}_{0}}}={\frac {2\pi }{\lambda }}\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/73821e313ba5c6f749792edaad70ba69052dc31b)
![{\displaystyle W=2Au_{a}^{2}R\left[1+{\frac {\sin(2kh)}{2kh}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c61c0c7483b62e0510bab6db4a734796cba55657)
![{\displaystyle W=Au_{1}^{2}R\left[1+\left({\frac {u_{2}^{2}}{u_{1}^{2}}}\right)+{\frac {2{{u}_{2}}}{{u}_{1}}}{\frac {\sin(2kh)}{2kh}}\cos \delta \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c271455b9ec11dd922eafd6cb6b590bc26dba8cd)








![{\displaystyle \phi (r,\theta ,t)={\frac {3{{F}_{z}}}{4\pi k{{Z}_{0}}}}\left[{\frac {1+ikr}{{r}^{2}}}\right]\cos \theta {{e}^{i(\omega t-kr)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d5433288c4aa534d458a1976b7981e26f515abce)


![{\displaystyle {\begin{aligned}&{{I}_{r}}(r,\theta )={\frac {9F_{z}^{2}}{16{{\pi }^{2}}{{Z}_{0}}}}\left[{\frac {{{k}^{2}}{{r}^{2}}}{{{r}^{4}}(1+{{k}^{2}}{{a}^{2}})}}=+i{\frac {2+{{k}^{2}}{{r}^{2}}}{{{r}^{4}}(1+{{k}^{2}}{{a}^{2}})kr}}\right]co{{s}^{2}}\theta \\&{{I}_{\theta }}(r,\theta )={\frac {i9F_{z}^{2}}{32{{\pi }^{2}}{{Z}_{0}}}}\left[{\frac {1+{{k}^{2}}{{r}^{2}}}{{{r}^{4}}(1+{{k}^{2}}{{a}^{2}})kr}}\right]sin2\theta \\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0842d36a36d888a65e0db69beb76a961c8af59b7)
![{\displaystyle W={\frac {3F_{z}^{2}}{4\pi {{a}^{2}}{{Z}_{0}}}}\left[{\frac {{{k}^{2}}{{a}^{2}}}{1+{{k}^{2}}{{a}^{2}}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a4d8a806d04578d204f18dca05da85cfdcead473)

![{\displaystyle p{{p}^{*}}={\frac {9F_{z}^{2}}{16{{\pi }^{2}}(1+{{k}^{2}}{{a}^{2}})}}\left[{\frac {(1+{{k}^{2}}r_{1}^{2})}{r_{1}^{4}}}{{\cos }^{2}}{{\alpha }_{1}}+{\frac {(1+{{k}^{2}}r_{2}^{2})}{r_{2}^{4}}}{{\cos }^{2}}{{\alpha }_{2}}+{\frac {2\cos {{\alpha }_{1}}\cos {{\alpha }_{2}}}{r_{1}^{2}r_{2}^{2}}}\left[(1+k{{r}_{1}}{{r}_{2}})\cos k({{r}_{2}}-{{r}_{1}})+k({{r}_{2}}-{{r}_{1}})\sin k({{r}_{2}}-{{r}_{1}})\right]\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ddacaf278928a5fe82cfdbe6dd75d4be89e84f21)




![{\displaystyle {\begin{aligned}&\varphi (r,\theta ,\psi ,t)={\frac {3F}{4\pi k{{Z}_{0}}}}\left[{\frac {{{k}^{2}}{{r}^{2}}-2(1+ikr)}{{r}^{3}}}\right]\cos \theta \sin \theta \cos \psi {{e}^{i(\omega t-kr)}}\\&p(r,\theta ,\psi ,t)={\frac {i3F}{4\pi }}\left[{\frac {{{k}^{2}}{{r}^{2}}-2(1+ikr)}{{r}^{3}}}\right]\cos \theta \sin \theta \cos \psi {{e}^{i(\omega t-kr)}}\\&{\overline {{p}^{2}}}(r,\theta ,\psi )={\frac {9{\overline {{\left({\frac {\partial F}{\partial t}}\right)}^{2}}}}{16{{\pi }^{2}}}}\left[{\frac {4+{{k}^{4}}{{r}^{4}}}{{r}^{6}}}\right]{{\cos }^{2}}\theta {{\sin }^{2}}{{\cos }^{2}}\psi \\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eb6ceed5f4392505cfd9188503024dd4c31890ef)



![{\displaystyle {\begin{aligned}&\varphi (r,\theta ,t)={\frac {3F}{4\pi k{{Z}_{0}}}}\left[{\frac {{{k}^{2}}{{r}^{2}}-2(1+ikr)}{{r}^{3}}}\right]{{\cos }^{2}}\theta {{e}^{i(\omega t-kr)}}\\&p(r,\theta ,t)={\frac {i3F}{4\pi }}\left[{\frac {{{k}^{2}}{{r}^{2}}-2(1+ikr)}{{r}^{3}}}\right]{{\cos }^{2}}\theta {{e}^{i(\omega t-kr)}}\\&{\overline {{p}^{2}}}(r,\theta )={\frac {9{\overline {{\left({\frac {\partial F}{\partial t}}\right)}^{2}}}}{16{{\pi }^{2}}}}\left[{\frac {4+{{k}^{4}}{{r}^{4}}}{{r}^{6}}}\right]{{\cos }^{4}}\theta \\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d444c5c2ff5c9d89cf361f3e3a3bcce3f2d97d60)
