代数/第 4 章/复合不等式和绝对值不等式

代数

代数/第 4 章
← 方程组	复合不等式和绝对值不等式	其他类型的图形 →

复合不等式是两个不等式作为同一个问题呈现。根据使用“和”或“或”的词语，被求解的变量可能只需要满足其中一个不等式或两者都需要满足。可能存在许多正确的答案，甚至可能完全没有答案。

示例：2x - 4 > 2 或 30/x > 15

然后可以将答案绘制为数轴上的两条射线。

如果我们对实数解感兴趣，我们可以选择几乎小于 2 或几乎大于 3 的数字，因为我们想要什么，方程都将成立。例如，如果 x =1.99，则 30/x = 15.08（满足 30/x > 15）或如果 x = 3.01，则 2x-4 = 2.02（满足 2x -4 > 2）。

如果我们只对整数解感兴趣，那么我们可以看到，除了 2 或 3 之外的所有整数都将起作用。

我们还可以将复合不等式表示为函数。

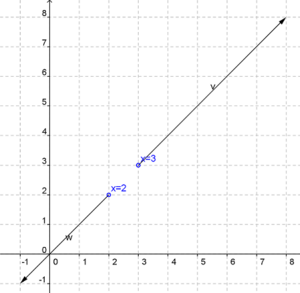
如果我们指定一个函数 f(x) = (x > 3 或 x < 2)，我们得到一个这样的图形

解仍然是两条射线。但是现在射线位于直线 y=x 上，一条射线从数字 3 向右向上移动，另一条射线从数字 2 向左向下移动。

练习：使用斜率的概念，你能解释为什么从数轴转移到笛卡尔图形的图形总是显示在直线 y=x 上吗？

如何使用复合不等式？

汽车上的燃油里程标签会给出两个数字：一个是城市驾驶，另一个是高速公路驾驶。如果标签说汽车在城市中能行驶 25 英里/加仑，在高速公路上能行驶 32 英里/加仑，那么你能行驶多远？

为了找出答案，我需要知道油箱里有多少油。我知道我可以用一加仑油行驶 25 到 32 英里。我可以使用两个方程来表示这一点，其中 x = 我可以用一加仑油行驶的距离

25 < x 且 x < 32。

或者我可以将它们组合成一个复合不等式

25 < x < 32。

如果我的油箱是 10 加仑，并且我想知道我能行驶多远，我会将方程改为表示我的油箱中 10 加仑油，方法是将复合不等式中的每一项乘以 10。

25 * 10 < 10*x < 32 * 10。

250 < 10x < 320。

我可以用一箱油行驶 250 到 320 英里。

华氏度到摄氏度的转换公式为 5/9(F - 32)。

我们知道水在 32 华氏度结冰，在 212 华氏度沸腾。

如果我们想知道水的冰点和沸点用摄氏度表示，我们可以将方程设置如下

32 < F < 212

然后应用公式将华氏度的值转换为摄氏度。

5/9(32-32) < C < 5/9(212 - 32)

所以水的冰点和沸点为

0 < C < 100

当我们需要乘以 x 时会发生什么？

请记住，减法等同于加一个负数，乘法等同于加一个数多次。因此，当我们多次加一个负数时，结果会越来越小。在使用不等式求解问题时，我们需要确定问题的背景对于负数是否合理。

一种特殊的复合不等式涉及绝对值符号。绝对值符号指定两个函数，使得 f(x)=A 意味着 f(-x) = (-A)(-1)。对于等号，这与 f(x)=f(-x)=A 相同。但是，当我们使用不等号并乘以负数时，我们必须改变符号的方向。因此，如果 f(x) > A，那么 f(-x) < A。

当只有 x 的值在绝对值符号中时，这很简单。例如，给出 |x| > 12，那么可能的解是 x > 12 或 x < -12。

三个绝对值问题的例子。
右边为正数	右边为零	右边为负数
$\|x\|-12>0$	$\|x\|+12>12$	$\|x\|+12>0$
$\|x\|>12$	$\|x\|>0$	$\|x\|>-12$
$x>12{\text{ or }}x<-12$	$x>0{\text{ or }}x<0$	${\text{all numbers }}x{\text{ satisfy }}\|x\|>-12$
12 和 -12 之间的间隙。	除了 0 之外的任何数字。	任何数字。