模拟电子/BJT/放大模式

放大模式

在发射极

回顾一下上一页，BJT在放大模式下，其发射极-基极结处于正向偏置，而集电极-基极结（CBJ）处于反向偏置。这意味着，对于NPN器件，发射极的电位低于基极，而基极的电位低于集电极。通常，集电极和基极之间的电压大于发射极和基极之间的电压。

EBJ处于正向偏置，因此电子将从发射极注入到基极。此外，一些空穴也将从基极注入到发射极，但发射极的掺杂浓度远高于基极，因此这种电流很小（这是理想的情况，因此晶体管的设计和制造方式就是这样）。

从发射极流出的电子和流入的空穴共同构成发射极电流，i_E，其定义为“从”发射极引线“流出”。正如我们之前所说，这种电流主要由电子流构成。

我们可能期望电子要么“卡住”在基极中，要么通过基极被移除，因为CBJ处于反向偏置，因此我们不希望它导通。但是，回想一下，当pn结像这样处于反向偏置时，这意味着空穴不能从左到右移动，而电子不能从右到左移动。通常，这会导致没有电流，因为p型材料中不存在电子。

在基极

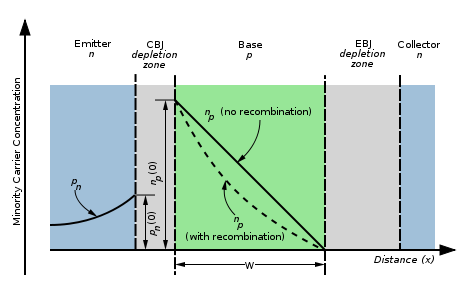
现在让我们看看注入到基极的电子发生了什么。因为基极是由p型硅制成的，所以电子是少数载流子。基极非常薄（上面的图不是按比例绘制的），因此电子浓度，n_p，将具有线性特性。这在半导体中解释过，我们这里不会试图证明它。电子浓度在基极的发射极侧最高，而在集电极侧为零。它在这里为零是因为CBJ处于反向偏置，导致所有少数载流子被吸引并扫过到集电极（同样，多数载流子，空穴，被排斥出结）。我们将基极EBJ侧的电子浓度称为n_p(0)。

EBJ处于正向偏置，因此基极发射极侧的浓度n_p(0) 将与e^v_BE/v_T 成正比。

[基极EBJ侧的电子浓度]

$n_{p}\left(0\right)=n_{p0}\exp \left({\frac {v_{BE}}{V_{T}}}\right)$

其中

• n_p0 是基极中电子的热平衡浓度
• v_BE 是EBJ上的正向电压
• V_T 是热电压（在室温 - 300K 下约为 25 mV）

随着我们向集电极移动，基极中电子浓度不断下降，导致了这个方向的扩散电流（电子试图扩散到浓度较低的区域）。这种扩散电流，I_n 与电子浓度梯度成正比

[基极中的电子电流]

$I_{n}=A_{E}qD_{n}{\frac {d\left({n_{p}\left(x\right)}\right)}{dx}}$

$I_{n}=A_{E}qD_{n}\left({-{\frac {n_{p}\left(0\right)}{W}}}\right)$

其中

• x 是某点到EBJ的距离
• A_E 是EBJ的横截面积
• q 是电子电荷的大小（正值）
• D_n 是基极中的电子扩散系数
• W 是基极的有效宽度（考虑到由于耗尽区而导致的减少）

有关确切原因的更多信息，请参阅半导体。

由于电子浓度的负斜率，我们得到一个负电流（相对于x），这意味着它从右到左流动。这并不奇怪，因为电子带负电，因此从左到右的扩散导致从右到左的电流。

因为这里的电子位于充满空穴的p型材料中，一些电子会在基极与空穴复合。由于基极非常薄，这只是电子总数的一小部分。这种效应导致基极中的电子浓度略微非线性（上图中的虚线）。因为浓度在EBJ附近较高，我们预计在EBJ处每单位长度有更多的电子复合，因此在EBJ处线更陡峭，导致图中所示的“凹陷”形状。

总之，我们从发射极向基极注入电子，这些电子很容易被CBJ上的电场扫过。基极的制造非常薄，以便只让这种情况发生。一小部分电子将与基极层中的空穴（多数载流子）复合。但是，基极非常薄，因此电子通常在复合之前就被扫过。这意味着会有大量的电流从发射极流过晶体管到基极。较小的电流由流入发射极的空穴和复合的空穴组成，构成基极电流。

这就是发射极和集电极的命名原因 - 发射极发射电子到基极，而集电极收集这些电子从基极。

集电极电流

在上面的部分中，我们看到，大多数扩散过基极的电子都到达CBJ，然后被CBJ上的电场扫过，CBJ处于反向偏置。这些“扫过”的电子构成了集电极电流，i_C 因此，我们可以说

$i_{C}=I_{n}\,$.

由于 *I_n* 为负值，这意味着集电极电流相对于我们增加 *x* 的方向也是负值。这意味着电流从右到左流动，因此流入集电极引线。在下式中，我们将删除负号，并使用电流的大小进行计算。

因此

$i_{C}=A_{E}qD_{n}\left({\frac {n_{p}\left(0\right)}{W}}\right)$

用上述的 *n_p*(0) 代入，我们得到

$I_{n}=A_{E}qD_{n}{\frac {n_{p0}\exp \left({v_{BE}/V_{T}}\right)}{W}}$

现在，我们定义一个称为 **饱和电流** 的量，如下所示

$I_{S}={\frac {A_{E}qD_{n}n_{p0}}{W}}$,

导致

[集电极电流]

$i_{C}=I_{S}\exp \left({\frac {v_{BE}}{V_{T}}}\right)$.

我们也可以将 *n_p0=n_i²/N_A* 代入我们对 *I_S* 的表达式

[饱和电流]

$I_{S}={\frac {A_{E}qD_{n}n_{i}^{2}}{N_{A}W}}$

请注意，集电极电流不依赖于 CBJ 上的电压 *v_CB*。只要 CBJ 处于反向偏置状态，到达 CBJ 的电子就会被移除到集电极中。

我们新定义的饱和电流 *I_S* 与基极宽度 *W* 成反比，与 EBJ 的面积成正比。饱和电流通常在 10⁻¹⁸ 到 10⁻¹² A 的范围内。它受温度影响很大，因为它与本征电子浓度的平方成正比。因此，它也与绝对温度的三次方成正比。这在 半导体 中有解释。对于实际的晶体管，饱和电流将由制造商在 数据手册 中给出。

由于饱和电流与 EBJ 面积与基极宽度之比有关，因此它也称为 **比例电流**。这是集成电路设计领域中经常使用的原理，因为两个除了 EBJ 面积外完全相同的晶体管，对于相同的 *v_BE*，其集电极电流将相差一个因子，该因子等于 EBJ 面积之比。

基极电流

我们已经看到基极电流有两个组成部分：注入到发射极的空穴 (*i_B1*) 和通过扩散提供的空穴（以补充那些与从发射极到集电极传输的电子复合的空穴）。这是 *i_B2*。

*i_B1* 由正向偏置的 *pn* 结的方程式给出，类似于之前使用的方程式

$i_{B1}={\frac {A_{E}qD_{p}n_{i}^{2}}{N_{D}L_{p}}}\exp \left({\frac {v_{BE}}{V_{T}}}\right)$

其中

• *A^E* 是 EBJ 的横截面积
• *L_p* 是空穴扩散长度
• *D_p* 是基极中的空穴扩散系数
• *N_D* 是发射极的掺杂浓度

请注意，由于发射极很长（与很短的基极相反），我们不使用发射极长度，而是使用 *L_p*，即空穴的扩散长度。

*i_B2* 可以通过查看基极中的电子复合所需的平均时间来评估。这段时间称为 **少数载流子寿命**，用 *τ_b* 表示。在这种情况下，在这段时间内，基极中所有电子（构成电荷 *Q_n*）将复合。

在稳态下，该电荷将由从发射极流入的电子不断补充。为了补充电子以保持稳态，注入电流必须为基极提供（正）电荷

[与少数载流子寿命相关的基极复合电流]

$i_{B2}={\frac {Q_{n}}{\tau _{b}}}$

稳态下存储在基极中的少数载流子电荷与由电子浓度曲线（这是一条直线）形成的三角形的面积有关，这可以在上面的图表中看到。乘以基极的体积、电子电荷和最大浓度 *n_p*(0)，我们得到总电荷为

$Q_{n}=A_{E}Wq\times {\frac {1}{2}}n_{p}\left(0\right).$

将n_p(0)代入，然后将n_p0代入得到

$Q_{n}={\frac {1}{2}}{\frac {A_{E}Wqn_{i}^{2}}{N_{A}}}\exp \left({\frac {v_{BE}}{V_{T}}}\right)$

将i_B2与τ_b相关的方程式代入，得到

$i_{B2}={\frac {1}{2}}{\frac {A_{E}Wqn_{i}^{2}}{\tau _{b}N_{A}}}\exp \left({\frac {v_{BE}}{V_{T}}}\right)$

现在，基极电流的总和为

$i_{B}=i_{B1}+i_{B2}$

$i_{B}={\frac {A_{E}qD_{p}n_{i}^{2}}{N_{D}L_{p}}}\exp \left({\frac {v_{BE}}{V_{T}}}\right)+{\frac {1}{2}}{\frac {A_{E}Wqn_{i}^{2}}{N_{A}\tau _{b}}}\exp \left({\frac {v_{BE}}{V_{T}}}\right)$

这个繁琐的形式可以通过应用饱和电流的表达式和提取指数部分来简化

$i_{B}=I_{S}\left({{\frac {D_{p}N_{A}W}{D_{n}N_{D}L_{p}}}+{\frac {1}{2}}{\frac {W^{2}}{D_{n}\tau _{b}}}}\right)\exp \left({\frac {v_{BE}}{V_{T}}}\right)$

顺便提一下，请注意i_B1所给出的部分与以下比率有关

• 空穴扩散率与电子扩散率之比
• 受主掺杂浓度与施主掺杂浓度之比
• 基极宽度与空穴在发射极中的扩散长度之比

我们现在定义一个称为β的量，如下所示

$\beta =1{\bigg /}\left({{\frac {D_{p}N_{A}W}{D_{n}N_{D}L_{p}}}+{\frac {1}{2}}{\frac {W^{2}}{D_{n}\tau _{b}}}}\right)$

β 是一个标量（见 这里 以确认），它完全由晶体管的物理性质决定。我们可以看到它将基极电流和集电极电流联系起来

$i_{B}={\frac {i_{C}}{\beta }}$.

对于“普通”晶体管，β 通常取值在 50 到 300 之间，但对于更昂贵的器件（尤其是那些以 IC 形式出售的器件，如 SSM2210），它可以达到 1000。β 通常被称为共射极电流增益。它也经常被称为h_FE。这是由于电路理论中的惯例。要了解原因，请参见 此页面。

我们可以看到，β 受一些与生产过程相关的参数而不是半导体的物理性质的影响。为了获得高β，我们可以使基极宽度W 非常小，并且与基极相比，发射极的掺杂浓度非常高。此外，请注意，到目前为止，我们假设β 在给定晶体管中是恒定的。我们很快就会看到，情况并非总是如此，但它通常是一个有用的近似值。

发射极电流

从基尔霍夫电流定律，我们知道所有进入晶体管的电流也必须离开晶体管。考虑到器件每个端子的“默认”电流方向，我们可以看到

$i_{E}=i_{B}+i_{C}$

利用i_B和i_C之间的关系，我们有

$i_{E}=i_{C}+{\frac {i_{C}}{\beta }}={\frac {\beta +1}{\beta }}i_{C}$

$i_{E}=I_{S}{\frac {\beta }{\beta +1}}\exp \left({\frac {v_{BE}}{V_{T}}}\right)$

我们也可以定义α，使得

$i_{C}=\alpha i_{E}$.

因此，α为

$\alpha ={\frac {\beta }{\beta +1}}$

我们可以很容易地从这里看到α小于但接近于1。用α替换i_E中的表达式，得到

$i_{E}=\left({\frac {I_{S}}{\alpha }}\right)\exp \left({\frac {v_{BE}}{V_{T}}}\right)$

重新排列α的表达式，我们也有

$\beta ={\frac {\alpha }{\alpha -1}}$

α被称为共基电流增益。α和β仅描述晶体管在正向激活模式下的工作（反向激活操作不同）。有时可能需要明确地显示这一点，通过写α_F和β_F。这些可以与α和β互换使用。

也可以使用能带图考虑BJT在激活模式下的工作。这种解释可以在此页面上找到。

大信号模型

在上一节中，我们看到了NPN BJT如何在正向激活模式下工作。也就是说，基极的电位高于发射极，集电极的电位高于基极。我们可以利用这些特性将BJT“转换”成更简单的组件进行分析。这些模型适用于所有信号，因此被称为大信号等效模型或LSEM。

共基LSEM

正向偏置的EBJ导致集电极中流过电流，该电流随基极-发射极电压v_BE呈指数关系变化。只要集电极的电位高于基极（因此CBJ处于反向偏置状态），此电流与集电极的电压无关。因此，BJT表现得像一个受v_BE控制的（非线性）电压控制电流源。

基极电流是发射极电流除以β得到的分数，发射极电流是集电极电流和基极电流的总和。通常，β很大，因此基极电流很小，发射极电流近似等于集电极电流。

从上面对NPN BJT的描述，我们可以推导出一个等效电路模型，该模型用更简单的组件来描述BJT。

二极管D_E中的电流为i_E。从上面，我们有

$i_{E}=\left({\frac {I_{S}}{\alpha }}\right)\exp \left({\frac {v_{BE}}{V_{T}}}\right)$

我们可以称$I_{S}/\alpha$为二极管的饱和电流I_{SE。之前我们已经确定集电极中的电流由以下公式给出

$i_{C}=i_{S}\exp \left({\frac {v_{BE}}{V_{T}}}\right)$

因此，我们可以看到i_C与i_E的关系是除以α。我们之前在推导出α的那一节也看到了这一点。

现在我们有一个BJT模型，它用v_BE来描述所有的电流，并参考基极电压。现在让我们将这个模型视为一个二端口网络，输入端口位于发射极和基极之间，输出端口位于集电极和基极之间。因此，基极是共用的。我们可以看到，电流增益等于α，因此α被称为共基电流增益。

共射LSEM

我们也可以有一个参考共发射极的BJT模型。

集电极电流由以下公式给出，与共基配置相同

$i_{C}=I_{S}\exp \left({\frac {v_{be}}{V_{T}}}\right)$

我们知道，基极电流由集电极电流除以β得出。

$i_{B}={\frac {I_{S}}{\beta }}\exp \left({\frac {v_{be}}{V_{T}}}\right)$

因此，我们可以很轻松地发现，集电极电流与基极电流的关系为

$i_{C}=\beta i_{B}$.

与之前一样，我们认为从基极到发射极的电流会通过内部二极管流动。这次，我们把它称为D_B，但现在它的饱和电流由下式给出：

$I_{SB}=I_{S}/\beta$