核医学基础物理/伽马射线衰减

康普顿效应

我们在上一章从描述的角度介绍了伽马射线与物质的相互作用，并发现康普顿效应和光电效应是主要的机制。我们将在本章再次考虑这个主题，但这次是从分析的角度。这将使我们能够对这种现象有更一般的理解。

注意，这里讨论的治疗也适用于X射线的衰减，因为正如我们之前提到的，伽马射线和X射线本质上是相同的物理实体。

我们的讨论从一个简单的辐射实验的描述开始，这个实验可以在实验室中轻松完成，许多早期领域的先驱者都做过这个实验。然后，我们将利用从这些实验中获得的信息来开发一个简单的方程和一些简单的概念，这些概念将使我们能够将情况推广到任何衰减情况。

衰减实验

实验很简单。它涉及到将一束狭窄的伽马射线射向一种材料，并测量有多少辐射穿透。我们可以改变我们使用的伽马射线的能量，以及吸收材料的类型及其厚度和密度。

下图显示了实验装置。我们将入射到吸收体的辐射强度称为入射强度，I₀，穿过吸收体的辐射强度称为透射强度，I_x。请注意，吸收体的厚度用x表示。

从我们在上一章中介绍的内容可以看出，一些伽马射线在穿过吸收体时会发生光电效应和康普顿效应等相互作用。透射的伽马射线主要是那些完全没有发生相互作用的伽马射线。

因此，我们可以预期透射强度将小于入射强度，即

$I_{x}<I_{0}\,\!$

但你可能会问，到底小多少呢？在我们考虑这一点之前，让我们将I_x和I₀之间的差值记为∆I，即

$\Delta I=I_{0}-I_{x}\,\!$

原子序数的影响

让我们从将不同的吸收体依次放置在辐射束中来开始探索∆I的大小。我们会发现∆I的大小高度依赖于吸收材料的原子序数。例如，我们会发现对于由碳（Z=6）制成的吸收体，∆I会相当低，而对于由铅（Z=82）制成的吸收体，∆I会非常大。

我们可以从下图了解为什么会出现这种情况

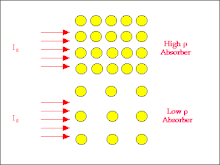
该图用大的圆圈代表原子，表示高原子序数的吸收体，用小的圆圈代表原子，表示低原子序数的材料。入射辐射束由从左侧进入每个吸收体的箭头表示。请注意，高原子序数吸收体的原子为辐射提供了更大的靶区，因此通过光电效应和康普顿效应发生相互作用的可能性相对较高。因此衰减应该相对较大。

然而，在低原子序数吸收体的情况下，单个原子更小，因此发生相互作用的可能性降低。换句话说，辐射更有可能穿过吸收体，因此衰减比高原子序数情况下的衰减低。

在我们在上一章中使用的宇宙飞船类比中，原子序数可以被认为是流星云中单个流星的大小。

如果我们能够精确控制实验装置并仔细分析我们的结果，我们会发现

$\Delta I\propto Z^{3}\,\!$

因此，如果我们将吸收体的原子序数增加一倍，我们就会将衰减增加到两倍的三次方，即8倍；如果我们将原子序数增加到三倍，我们就会将衰减增加到三倍的三次方，即27倍，等等。

正是由于这个原因，高原子序数材料（例如Pb）被用于辐射防护。

密度的影响

探索∆I大小的第二种方法是观察当我们改变吸收体密度时会发生什么。我们可以从下图看到，低密度吸收体产生的衰减比高密度吸收体产生的衰减小，因为辐射与吸收体原子之间发生相互作用的可能性相对较低。此外，密度决定了与样品相关的透射系数，因为密度越低，透射系数越高，因为材料的孔隙率更高。

因此，在宇宙飞船进入流星云的类比中，想象一下不同密度的流星云以及宇宙飞船与流星发生碰撞的可能性。

厚度的影响

我们可以改变的第三个因素是吸收体的厚度。正如你应该能够在这个阶段预测的那样，吸收体越厚，衰减越大。

伽马射线能量的影响

在我们的实验中，我们能够改变伽马射线束的能量。我们发现，虽然不深入探讨细节，但伽马射线的能量越高，衰减越小。你可以把它想象成宇宙飞船以不同的能量接近流星云，能量低的宇宙飞船穿过的可能性较小，而能量高的宇宙飞船穿过的可能性较大。

数学模型

这里我们将考虑一个数学模型，它将帮助我们用更一般的术语表达我们的实验观察结果。你会发现，采用的数学方法和得到的结果与我们之前在放射性衰变定律中遇到的非常相似。所以你不需要再费力地学习新的数学知识，只需要对相同形式的数学分析进行不同的应用！

让我们从最简单的情况开始，假设我们只改变吸收体的厚度。换句话说，我们使用相同材料（即相同原子序数）和相同密度的吸收体，并使用相同能量的伽马射线进行实验。只有吸收体的厚度发生了改变。

从我们上面的推理中不难理解，∆I 的大小应该取决于辐射强度以及吸收体的厚度，也就是说，对于吸收体厚度微小的变化

$-dI\propto I\cdot dx\,\!$

负号表示强度因吸收体而减小。

将这个等式中的比例关系转化为等式，我们可以写成

$-dI=\mu I\cdot dx\,\!$

其中比例常数 μ 称为线性衰减系数。

除以 I，我们可以将这个等式改写为

$-{\frac {dI}{I}}=\mu \cdot dx$

所以这个等式描述了对于任何微小的吸收体厚度变化 dx 的情况。要找出对于吸收体的完整厚度会发生什么，我们只需将每个小厚度上发生的情况加起来即可。换句话说，我们将上述等式积分。更正式地表达，我们可以说，对于从 x = 0 到任何其他厚度 x 的厚度，辐射强度将从 I₀ 减少到 I_x，因此

$-\int _{I_{0}}^{I_{x}}{\frac {dI}{I}}=\mu \int _{0}^{x}dx$

$\therefore \ln \left({\frac {I_{x}}{I_{0}}}\right)=-\mu x$

$\therefore {\frac {I_{x}}{I_{0}}}={\text{exp}}\ (-\mu x)$

$\therefore I_{x}=I_{0}\ {\text{exp}}\ (-\mu x)\,\!$

这个最终的表达式告诉我们，辐射强度将随着吸收体的厚度以指数方式减小，减小的速率由线性衰减系数控制。该表达式在下面的图形中显示。该图绘制了强度与厚度 x 的关系。我们可以看到，强度从 I₀ 开始减小，即 x = 0 处的数值，最初以较快的速度减小，然后以经典的指数方式减慢。

辐射强度对吸收体厚度的依赖关系的图形表示：左侧为强度与厚度的关系，右侧为强度自然对数与厚度的关系。

线性衰减系数的影响可以在下一张图中看到。这里的所有三条曲线都是指数性质的，只有线性衰减系数不同。注意，当线性衰减系数较小时，曲线下降得比较慢，当线性衰减系数较大时，曲线下降得很快。

使用小、中、大线性衰减系数 µ 表示的指数衰减。

线性衰减系数是单个吸收材料的特征。有些材料，比如碳，其值较小，很容易被伽马射线穿透。其他材料，比如铅，其线性衰减系数相对较大，是相对较好的辐射吸收体。

各种材料在 100、200 和 500 keV 伽马射线能量下的线性衰减系数 (cm^-1)。

吸收体	100 keV	200 keV	500 keV
空气	0.000195	0.000159	0.000112
水	0.167	0.136	0.097
碳	0.335	0.274	0.196
铝	0.435	0.324	0.227
铁	2.72	1.09	0.655
铜	3.8	1.309	0.73
铅	59.7	10.15	1.64

上表中列出的材料为空气、水以及从碳 (Z=6) 到铅 (Z=82) 的一系列元素，并给出了三种伽马射线能量下的线性衰减系数。第一个需要注意的是，线性衰减系数随着吸收体原子序数的增加而增加。例如，它从空气在 100 keV 下的 0.000195 cm^-1 的很小的值增加到铅的近 60 cm^-1。第二个需要注意的是，所有材料的线性衰减系数都随着伽马射线能量的增加而减小。例如，铜的值从 100 keV 下的约 3.8 cm^-1 减少到 500 keV 下的 0.73 cm^-1。第三个需要注意的是，表中的趋势与前面介绍的分析一致。

最后，重要的是要认识到，我们上面的分析只在处理狭窄的辐射束时才严格成立。当涉及到宽辐射束时，需要考虑其他因素。

半值层

与使用半衰期描述放射性衰变定律一样，通常从上面的指数衰减方程中推导出一个指标，它有助于我们更清楚地理解正在发生的事情。这个指标称为半值层，它表示将入射辐射强度降低一半所需的吸收材料厚度。从图形的角度来看，我们可以说，当

$I_{x}={\frac {I_{0}}{2}}$

吸收体的厚度是半值层

下表列出了三种伽马射线能量下各种吸收体的半值层

三种伽马射线能量下各种材料的半值层（单位：厘米）。

吸收体	100 keV	200 keV	500 keV
空气	3555	4359	6189
水	4.15	5.1	7.15
碳	2.07	2.53	3.54
铝	1.59	2.14	3.05
铁	0.26	0.64	1.06
铜	0.18	0.53	0.95
铅	0.012	0.068	0.42

首先要注意的是，半值层随着原子序数的增加而减小。例如，空气在 100 keV 的半值层约为 35 米，而铅在该能量下的半值层仅为 0.12 毫米。换句话说，需要 35 米的空气才能将 100 keV 伽马射线束的强度降低一半，而 0.12 毫米的铅就能做到同样的事情。第二点要注意的是，半值层随着伽马射线能量的增加而增加。例如，铜在 100 keV 的半值层为 0.18 厘米，而在 500 keV 的半值层约为 1 厘米。第三点要注意的是，相对于上一张表格中的数据，半值层和线性衰减系数之间存在倒数关系，我们现在将对其进行研究。

μ 和半值层之间的关系

正如我们在放射性衰变定律中探索了半衰期和衰变常数之间的关系一样，我们也可以推导出半值层和线性衰减系数之间的关系。我们可以通过使用半值层的定义来实现这一点

$I={\frac {I_{0}}{2}}$

当

$x=x_{\frac {1}{2}}$

并将它代入指数衰减方程，即

$I=I_{0}\ {\text{exp}}\ (-\mu x)\,\!$

得到

${\frac {I_{0}}{2}}=I_{0}\ {\text{exp}}\ (-\mu x_{\frac {1}{2}})$

因此

${\frac {1}{2}}={\text{exp}}\ (-\mu x_{\frac {1}{2}})$

$\therefore 2^{-1}={\text{exp}}\ (-\mu x_{\frac {1}{2}})$

$\therefore \ln 2^{-1}=-\mu x_{\frac {1}{2}}$

$\therefore \ln 2=\mu x_{\frac {1}{2}}$

$\therefore 0.693=\mu x_{\frac {1}{2}}$

$\mu ={\frac {0.693}{x_{\frac {1}{2}}}}$

和

$x_{\frac {1}{2}}={\frac {0.693}{\mu }}$

这两个公式表达了线性衰减系数和半值层之间的关系。在解决与衰减相关的数值问题时，它们非常有用，并且通常是解决数值问题的第一步。

质量衰减系数

我们在上面暗示了线性衰减系数在考虑相同密度但不同厚度的吸收材料时非常有用。当我们希望将吸收体的密度 ρ 纳入分析时，一个相关的系数可能会有价值。这就是质量衰减系数，定义为

${\frac {\text{Linear Attenuation Coefficient}}{\text{Density}}}={\frac {\mu }{\rho }}$

上面表格中使用的线性衰减系数的测量单位是 cm^-1，密度的常用单位是 g cm^-3。您可能想根据此基础自行推导出 cm² g^-1 是质量衰减系数的等效单位。

问题

下面给出两个问题，以帮助您加深对本章内容的理解。第一个问题比较直接，将锻炼您对指数衰减公式的应用。第二个问题更具挑战性，将帮助您将指数衰减与放射性和辐射照射联系起来。

问题 1

需要多少铝才能将 200 keV 伽马射线束的强度降低到其入射强度的 10%？假设 200 keV 伽马射线在 Al 中的半值层为 2.14 cm。

答案

用上述符号表示的问题是

$I={\frac {I_{0}}{10}},\ {\text{when}}\ x={\text{?}}$

我们知道半值层为 2.14 cm。因此，线性衰减系数为

$\mu ={\frac {0.693}{x_{\frac {1}{2}}}}={\frac {0.693}{2.14}}=0.324\ {\text{cm}}^{-1}$

现在将所有这些与指数衰减公式结合起来

$I=I_{0}\ {\text{exp}}\ (-\mu x)\,\!$

我们可以写

${\frac {I_{0}}{10}}=I_{0}\ {\text{exp}}\ (-0.324x)$

因此

${\frac {1}{10}}={\text{exp}}\ (-0.324x)$

$\therefore -\ln 10=-0.324x$

$\therefore x={\frac {\ln 10}{0.324}}={\frac {2.3}{0.324}}=7.1\ {\text{cm}}$

$\therefore x\approx 7\ {\text{cm}}$

因此，将这些伽马射线降低十倍所需的铝厚度约为 7 厘米。这种相对较大的厚度是铝通常不用于辐射防护的原因 - 它的原子序数不足以有效地显着衰减伽马射线。

您可以尝试将 Pb 作为吸收体的情况 - 但您需要自己找出 200 keV 伽马射线在 Pb 中的半值层！

这里有一个提示：查看上面的表格之一。

以下为您提供答案，供您检查完成后核对：2.2 毫米。

换句话说，需要相对较薄的 Pb 厚度才能达到与 7 厘米铝相同的效果。

问题 2

一个 10⁵ MBq 的¹³⁷Cs 源需要装在 Pb 盒子里，以便源头 1 米处的照射率小于 0.5 mR/小时。如果¹³⁷Cs 伽马射线在 Pb 中的半值层为 0.6 厘米，则需要多厚的 Pb？¹³⁷Cs 的比伽马射线常数在 1 厘米处为 3.3 R hr^-1 mCi^-1。

答案

这是一个相当典型的例子，它出现在人们使用放射性物质时。我们希望使用一定量的物质，并将它储存在铅容器中，以便在安全距离内工作的照射率低于某个安全水平。我们知道将要使用的物质的放射性。但它用 SI 单位表示。我们查阅参考书，发现该放射性同位素的照射率以传统单位表示。就像我们的问题一样！

因此，让我们首先将单位统一。比伽马射线常数给出为

3.3 R hr^-1 mCi^-1 在距离源头 1 厘米处。

这等于

3300 mR hr^-1 mCi^-1 在距离源头 1 厘米处，

这等于

${\frac {3300}{(100)^{2}}}\ {\text{mR hr}}^{-1}\ {\text{mCi}}^{-1}\ {\text{at 1 m from the source}}$

基于平方反比定律。该结果按贝克勒尔表示为

${\frac {3300}{10^{4}(3.7\cdot 10^{7})}}\ {\text{mR hr}}^{-1}\ {\text{Bq}}^{-1}\ {\text{at 1 m from the source}}$

因为 1 mCi = 3.7 x 10⁷ Bq。因此，对于 10⁵ MBq，曝光率为

${\frac {3300\cdot 10^{5}\cdot 10^{6}}{10^{4}(3.7\cdot 10^{7})}}\ {\text{mR hr}}^{-1}\ (10^{5}\ {\text{MBq}})^{-1}\ {\text{at 1 m from the source}}$

也就是说，我们源头1米处的曝光率为891.9 mR hr^-1。

我们希望根据问题将该曝光率降低到 0.5 mR hr^-1以下，使用铅来实现。

在此阶段，您应该能够使用指数衰减方程和这些伽马射线在铅中的半值层来计算所需的铅厚度约为6.5 厘米。

外部链接

• Mucal on the Web - 由伊利诺伊理工学院同步辐射研究与仪器中心 Pathikrit Bandyopadhyay 提供的在线程序，用于计算 X 射线吸收系数。
• Tables of X-Ray Mass Attenuation Coefficients - 来自美国国家标准与技术研究院的大量数据，涵盖所有元素。