计算资源效率的提高和成本的降低对建模和设计产生了巨大的影响。强大的计算机工作站和软件或编程语言(例如,MATLAB、LabView、wxMaxima、R 等等)的易用性允许交互式设计高性能、鲁棒的控制器。故障风险往往阻碍了在活人身上设计和评估控制器的可能性,因此,设备和治疗方法通常首先在计算机和动物模型上进行测试。过去,动物一直是首选,但这种方法不断受到重新评估,因为动物很少是人类疾病和状况的完美模型。组织培养开始满足这种需求的一部分,计算机建模和仿真也可以做到这一点。如今,计算机模型被用于 (1) 证明可行性,(2) 通过补充动物研究来提高对控制器设计的信心,(3) 帮助设计更好的动物和临床实验,以及 (4) 减少所需的动物和人体实验数量。未来,计算机模型的应用将进一步扩展。
这种分析涉及将生理系统划分为若干相互连接的隔室 - 其中隔室可以是系统的任何解剖学、生理学、化学或物理亚部分。一个基本假设是示踪剂在整个隔室中均匀分布。在各种隔室模型中,最简单的模型是单隔室模型。
 图 4.1. 单隔室模型
图 4.1. 单隔室模型
 图 4.2. 示踪剂数量 q 相对于时间变化的图形说明,对应于相对高和低的周转率 k 值。
图 4.2. 示踪剂数量 q 相对于时间变化的图形说明,对应于相对高和低的周转率 k 值。
图 4.1 显示了一个单隔室模型,其中示踪剂通过血管的流动遵循理想的脉冲注射。该系统中的隔室是封闭的,除了示踪剂的流入和流出,示踪剂被注射,如图所示。在这个理论中,示踪剂将根据其注射立即并均匀地在整个隔室中混合。其数量将随着时间的推移而减少,这取决于流出率。该系统中使用的变量是
q:时间 t 时隔室中示踪剂的数量,以及
F:流出量。
如果我们将周转率 k 定义为这两个参数的比率,即

它可以改写为

该方程的解是

其中 qo 是时间 t = 0 时存在的示踪剂数量。该方程在图 4.2 中绘制。
 图 4.3 封闭双隔室模型
图 4.3 封闭双隔室模型
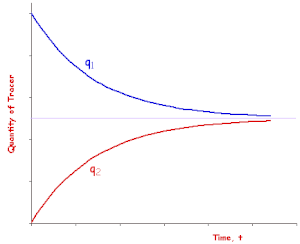 图 4.4 封闭隔室模型中隔室 #1 和 #2 中示踪剂数量随时间的变化。
图 4.4 封闭隔室模型中隔室 #1 和 #2 中示踪剂数量随时间的变化。
在封闭系统中,示踪剂只是在两个隔室之间移动,没有整体的损失或增益,如图 4.3 所示。因此,
 和
和  .
.
由于系统中没有示踪剂损失,

因此,

随着隔室 #1 中示踪剂数量的减少,隔室 #2 中的数量会增加,反之亦然。当示踪剂在时间 t = 0 时被注射到隔室 #1 中时,
 |
和 |

|
因此,在初始阶段
 |
和 |

|
该系统的解为

和

图 4.4 显示了如果隔室体积相同,则这些系统之一。
两个隔室像链一样连接,最后一个隔室有一个汇,如图 4.5 所示。
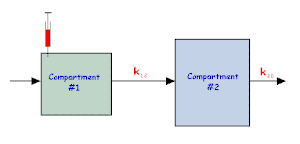 图 4.5 开放链状双隔室模型。
图 4.5 开放链状双隔室模型。
 图 4.6 开放链状双隔室模型中示踪剂数量随时间的变化。
图 4.6 开放链状双隔室模型中示踪剂数量随时间的变化。
在这个模型中,
 和
和 
这些方程的解为

和

并且 q1 和 q2 的行为如图 4.6 所示。
中央隔室有一个汇,它与其他隔室无关。虽然这些隔室不一定具有生理意义,但常见的名称是
- 隔室 1(中央) - 血液和良好灌注的器官,例如肝脏、肾脏等;“血浆”
- 隔室 2(外围) - 灌注不良的组织,例如肌肉、瘦肉组织、脂肪;“组织”
 图 4.7 开放乳头状双隔室模型。
图 4.7 开放乳头状双隔室模型。
 图 4.8 开放乳头状双隔室模型中示踪剂数量随时间的变化。
图 4.8 开放乳头状双隔室模型中示踪剂数量随时间的变化。
在这种情况下,
 和
和 
当 *t* = 0 时
 和
和 
所以,解为
 和
和

 心血管系统建模
心血管系统建模
另请参阅 人类呼吸控制系统数学模型
 呼吸系统建模
呼吸系统建模
另请参阅 用于控制人类运动的分布式神经网络:来自正常人和脊髓损伤患者的经验教训。
术语“神经网络”通常指的是一类计算算法,这些算法松散地基于神经系统的计算结构。换句话说,神经网络的设计包括指定神经元、架构和学习算法。
另请参阅 运动的外部控制
另请参阅 维基百科,眼动
- 生物学与医学中的区室分析,第 2 版,密歇根大学出版社,1985 年。
- Evans, W. C.,线性系统、隔室模型和 IAQ 研究中的可估计性问题,见 Tichenor, B.,室内空气污染源及其相关汇效应特征,ASTM STP 1287,第 239-262 页,1996 年 ISBN 0-8031-2030-3。
- Bronzino J. (编) 生物医学工程手册,3 卷套。 (第 3 版,CRC,2006)ISBN 0849321212































