微积分/极坐标积分

简介

对极坐标方程进行积分需要与笛卡尔坐标系下的积分不同的方法，因此产生了不同的公式，这不像直接对函数 $f(x)$ 进行积分那样直接。

证明

在创建积分概念时，我们使用矩形的黎曼和来逼近曲线下的面积。然而，对于极坐标图，可以使用半径为 $r$ ，角度为 $d\theta$ 的圆形扇形来逼近面积。每个扇形的面积为 $\pi r^{2}{\frac {d\theta }{2\pi }}$ ，所有无限小的扇形面积之和为： ${\frac {1}{2}}\int \limits _{a}^{b}r^{2}d\theta$ 。这是用于对形式为 $r=f(\theta )$ 的极坐标表达式进行积分的公式，其中 $(a,f(a))$ 和 $(b,f(b))$ 是你想要积分的曲线的端点。

积分学

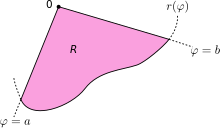积分区域 $R$ 由曲线 $r=f(\theta )$ 和射线 $\theta =a$ 和 $\theta =b$ 所包围。

令 $R$ 表示曲线 $r=f(\theta )$ 和射线 $\theta =a$ 和 $\theta =b$ 所包围的区域，其中 $0<b-a<2\pi$ 。然后，$R$ 的面积是

${\frac {1}{2}}\int \limits _{a}^{b}r^{2}d\theta$

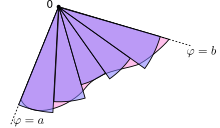区域 R 用 n 个扇形来近似（这里，n = 5）。

该结果可以如下得出。首先，区间 $[a,b]$ 被分成 $n$ 个子区间，其中 $n$ 是任意正整数。因此，每个子区间的长度 $\theta$ 等于 $b-a$ （区间的总长度），除以 $n$ ，即子区间的数量。对于每个子区间 $i=1,2,\dots ,n$ ，设 $\theta _{i}$ 为子区间的中点，并构造一个圆心位于原点、半径为 $r_{i}=f(\theta _{i})$ 、中心角为 $\delta \theta$ 、弧长为 $r_{i}\delta \theta$ 的扇形。因此，每个扇形的面积都等于 ${\tfrac {1}{2}}r_{i}^{2}\delta \theta$ 。因此，所有扇形的总面积为

$\sum _{i=1}^{n}{\tfrac {1}{2}}r_{i}^{2}\delta \theta$

随着子区间数量 $n$ 的增加，面积的近似值不断提高。当 $n\to \infty$ 时，该和式变为黎曼积分。

泛化

使用笛卡尔坐标，微分面积元可以计算为 $dA=dx\,dy$ 。多元积分的替换规则指出，当使用其他坐标时，必须考虑坐标转换公式的雅可比行列式

$J=\det {\frac {\partial (x,y)}{\partial (r,\theta )}}={\begin{vmatrix}{\dfrac {\partial x}{\partial r}}&{\dfrac {\partial x}{\partial \theta }}\\{\dfrac {\partial y}{\partial r}}&{\dfrac {\partial y}{\partial \theta }}\end{vmatrix}}={\begin{vmatrix}\cos(\theta )&-r\sin(\theta )\\\sin(\theta )&r\cos(\theta )\end{vmatrix}}=r\cos ^{2}(\theta )+r\sin ^{2}(\theta )=r$

因此，极坐标中的面积元素可以写成

$dA=J\,dr\,d\theta =r\,dr\,d\theta$

现在，以极坐标形式给定的函数可以按如下方式积分

$\iint _{R}g(r,\theta )dA=\int \limits _{a}^{b}\int \limits _{0}^{r(\theta )}g(r,\theta )\,r\,dr\,d\theta$

这里，R 与上面相同，即曲线 $r=f(\theta )$ 和射线 $\theta =a$ 和 $\theta =b$ 所包围的区域。

通过将 $g$ 完全等于 1，可以得到上面提到的 $R$ 面积公式。

应用

当相应的积分难以或无法用笛卡尔坐标进行时，极坐标积分通常很有用。例如，让我们尝试找到封闭单位圆的面积。也就是说，$x^{2}+y^{2}=1$ 所包围区域的面积。

在笛卡尔坐标系中

模板：组织部分

$\int \limits _{-1}^{1}\int \limits _{-{\sqrt {1-x^{2}}}}^{\sqrt {1-x^{2}}}\,dy\,dx=2\int \limits _{-1}^{1}{\sqrt {1-x^{2}}}dx$

为了评估这一点，通常使用三角替换法。通过设置 $\sin(\theta )=x$，我们得到 $\cos(\theta )={\sqrt {1-x^{2}}}$ 和 $\cos(\theta )d\theta =dx$。

${\begin{aligned}\int {\sqrt {1-x^{2}}}dx&=\int \cos ^{2}(\theta )d\theta \\&=\int {\frac {1+\cos(2\theta )}{2}}d\theta \\&={\frac {\theta }{2}}+{\frac {\sin(2\theta )}{4}}+C={\frac {\theta }{2}}+{\frac {\sin(\theta )\cos(\theta )}{2}}+C&={\frac {\arcsin(x)+x{\sqrt {1-x^{2}}}}{2}}+C\end{aligned}}$

将此代回方程，我们得到

$2\int \limits _{-1}^{1}{\sqrt {1-x^{2}}}dx=2\left[{\frac {\arcsin(x)+x{\sqrt {1-x^{2}}}}{2}}\right]_{-1}^{1}=\arcsin(1)-\arcsin(-1)=\pi$

在极坐标下

为了在极坐标下进行积分，我们首先意识到 $r={\sqrt {x^{2}+y^{2}}}={\sqrt {1}}=1$，并且为了包含整个圆，$a=0$ 和 $b=2\pi$。

$\int \limits _{0}^{2\pi }\int \limits _{0}^{1}r\,dr\,d\theta =\int \limits _{0}^{2\pi }\left[{\frac {r^{2}}{2}}\right]_{0}^{1}d\theta =\int \limits _{0}^{2\pi }{\frac {d\theta }{2}}=\left[{\frac {\theta }{2}}\right]_{0}^{2\pi }={\frac {2\pi }{2}}=\pi$

一个有趣的例子

极坐标积分的一个不太直观的应用可以得到高斯积分

$\int \limits _{-\infty }^{\infty }e^{-x^{2}}dx={\sqrt {\pi }}$

试试看！(提示：将 $\int \limits _{-\infty }^{\infty }e^{-x^{2}}dx$ 与 $\int \limits _{-\infty }^{\infty }e^{-y^{2}}dy$ 相乘。)