微积分
外观
欢迎来到华夏公益教科书的
微积分
| 一位华夏公益教科书用户建议将 微积分课程 合并到本书中。 在 讨论页面 上讨论是否应该进行此合并。 |
本华夏公益教科书旨在成为一本高质量的 微积分 教科书,用户可以通过它掌握这门学科。涵盖了极限、微分和积分等标准主题,以及其他几个主题。请在您认为有必要的地方进行 贡献。您只需通过对您认为评分不当的书籍的各个部分进行评分来帮助我们!


积分
[edit | edit source]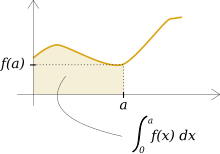
积分基础
[edit | edit source]积分技巧
[edit | edit source]
- 加速度函数 a(t);
- 加速度的积分是速度函数 v(t);
- 速度的积分是距离函数 s(t)。
积分应用
[edit | edit source]
参数方程
[edit | edit source]极坐标方程
[edit | edit source]数列和级数
[edit | edit source]数列
[edit | edit source]级数和检验方法
[edit | edit source]

7.11 反函数定理,隐函数定理 (可选)
- 旧: 二重积分
- Lester R. Ford, Sr. & Jr. (1963) 微积分, McGraw-Hill via HathiTrust
- w:Mellen W. Haskell (1895) 关于引入双曲函数的概念 美国数学会通报 1(6):155–9.
