变分法/第一章

第一章：变分法主要问题的介绍。

• 1 变分法与极值理论之间的联系。

问题 I. 围绕给定轴旋转时，生成最小表面积的曲线。

• 2,3,4 用极值方法解决此问题。
• 5,6 变分法与极值理论的区别。
• 7 坐标 $x$, $y$ 表示为参数 $t$ 的函数。以参数 $t$ 形式描述的 问题 I。
• 8,9 问题 II. 最速降线。
• 10 问题 III. 给定曲面上的最短线。
• 11 以参数 $t$ 形式描述问题的优势。
• 12 问题 IV. 最小阻力的旋转曲面。
• 13 一般问题的陈述。
• 14 端点的变化。
• 15 问题 V. 等周问题。
• 16 问题 VI. 重心最低的曲线。
• 17 相对极值中一般问题的陈述。
• 18 可能做出的概括。
• 19 曲线的变分。最大值和最小值的解析定义。邻近曲线。
• 20 一般问题的另一种陈述。
• 21 最大值或最小值预设存在的不允许性。
• 问题

第 1 条.
在微积分，以及部分积分学被推导出来的时候，提出了一些问题，这些问题虽然不属于极值理论的范畴，但与该理论的问题有着明显的相似之处，而且通常可以用属于该理论的方法来解决。以下是其中第一个被提出的问题。

问题 I. 给定两点 $P_{0}$ 和 $P_{1}$，其坐标分别为 $(x_{0},y_{0})$ 和 $(x_{1},y_{1})$。这两点都在 $X$ 轴的同一侧的平面上 -$xy$（包括 $X$ 轴）。要求用一条位于 $xy$ 平面（包括 $X$ 轴）上半部分的曲线连接 $P_{0}$ 和 $P_{1}$，使得当平面绕 $X$ 轴旋转一圈时，该曲线生成的旋转曲面具有最小的表面积。

我们可以用这个问题来说明变分法与极值理论之间的联系；同时，这两种理论之间的区别也显而易见。

第 2 条.
如果我们尝试用极值理论的方法来解决上一条中的问题，我们必须按以下步骤进行。

假设可以在 $P_{0}$ 和 $P_{1}$ 之间绘制一条曲线，满足问题要求。那么这条曲线的每一部分，无论多么小，都必须具有产生最小面积表面的性质。因为，假设在曲线的任意一部分进行改变，无论多么小，并且让曲线的其余部分保持不变。如果通过这种改变，由曲线这部分产生的表面积比以前小，那么包含变形部分的曲线产生的表面积小于原始曲线。此外，如果对于 $x$ 的一个值对应于 $y$ 的多个值，那么，而不是取属于相同横坐标的曲线部分，我们可以取连接这两个点的直线。这条直线产生的表面积小于通过相同两点的曲线产生的表面积。因此，曲线将产生一个没有最小面积的表面。因此，我们可以将曲线视为被分成几部分，使得这些部分在 $X$ 轴上的投影都相等。

第三条.
在上述假设的基础上，我们假设在曲线上取两点 $P'(x',y')$ 和 $P''(x'',y'')$，并在曲线上找到另一个点 $P(x,y)$，使得 $x-x'=x''-x=\Delta x$。我们假设用直线将 $P$ 和 $P'$，$P$ 和 $P''$ 连接起来，然后假设这些直线彼此靠得很近，以至于它们从直线过渡到曲线。假设在 $P'$ 左侧和 $P''$ 右侧的曲线其余部分保持不变。

直线 $P'P$ 和 $PP''$ 产生的表面积部分为

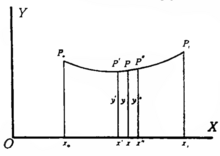
$\pi (y'+y){\sqrt {(\Delta x)^{2}+(y-y')^{2}}}$ 和 $\pi (y+y''){\sqrt {(\Delta x)^{2}+(y''-y)^{2}}}$

为了使这两个表达式相加后对y求导的和为零，即最小值，

$\pi {\sqrt {(\Delta x)^{2}+(y-y')^{2}}}+\pi {\sqrt {(\Delta x)^{2}+(y''-y)^{2}}}+{\frac {\pi (y'+y)(y-y')}{\sqrt {(\Delta x)^{2}+(y-y')^{2}}}}-{\frac {\pi (y+y'')(y''-y)}{\sqrt {(\Delta x)^{2}+(y''-y)^{2}}}}=0\qquad {\text{[A]}}$

量 $y$ 可以从这个等式中作为 $x$ 的函数确定，因此，假设 $y=f(x)$。因此我们有 $y'=f(x-\Delta x)$ 和 $y''=f(x+\Delta x)$。因此，根据泰勒定理，

$y'=f(x-\Delta x)=f(x)-f'(x)\Delta x+{\frac {1}{2}}f''(x)(\Delta x)^{2}-\cdots$

$y''=f(x+\Delta x)=f(x)+f'(x)\Delta x+{\frac {1}{2}}f''(x)(\Delta x)^{2}+\cdots$

因此，

$y-y'=f'(x)\Delta x-{\frac {1}{2}}f''(x)(\Delta x)^{2}+\cdots$

$y''-y=f'(x)\Delta x+{\frac {1}{2}}f''(x)(\Delta x)^{2}+\cdots$

将这些值代入[A]中，忽略因子 $\pi$，

$\Delta x{\sqrt {1+f'(x)^{2}-f'(x)f''(x)\Delta x+\cdots }}+\Delta x{\sqrt {1+f'(x)^{2}+f'(x)f''(x)\Delta x+\cdots }}$

$+{\frac {[2f(x)-f'(x)\Delta x+\cdots ][f'(x)\Delta x-{\frac {1}{2}}f''(x)\Delta x+\cdots ]}{\Delta x{\sqrt {1+f'(x)^{2}-f'(x)f''(x)\Delta x+\cdots }}}}+{\frac {[2f(x)+f'(x)\Delta x+\cdots ][f'(x)\Delta x+{\frac {1}{2}}f''(x)\Delta x+\cdots ]}{\Delta x{\sqrt {1+f'(x)^{2}+f'(x)f''(x)\Delta x+\cdots }}}}=0$

将此表达式按 $\Delta x$ 的升幂展开，并除以 $\Delta x$，然后令 $\Delta x=0$。然后我们有

$1+f'(x)^{2}-f(x)f''(x)=0$;

或者

$1+\left({\frac {{\text{d}}y}{{\text{d}}x}}\right)^{2}-y{\frac {{\text{d}}^{2}y}{{\text{d}}x^{2}}}=0\qquad {\text{[B]}}$

因此，为了使 $f(x)$ 或 $y$ 具有最小值，它必须满足这个微分方程；但是，当 $y$ 满足这个微分方程时，并不总是存在最小值，这将在后面说明。

换句话说，微分方程 [B] 是旋转最小曲面的假设存在性的必要结果。但是，作为一个条件，它不足以保证存在一条曲线来生成这样的曲面。

对方程 [B] 关于 $x$ 求导，我们有

${\frac {{\text{d}}y}{{\text{d}}x}}\cdot {\frac {{\text{d}}^{2}y}{{\text{d}}x^{2}}}=y{\frac {{\text{d}}^{3}y}{{\text{d}}x^{3}}}$,

或者

${\frac {\frac {{\text{d}}y}{{\text{d}}x}}{y}}={\frac {{\frac {\text{d}}{{\text{d}}x}}\left({\frac {{\text{d}}^{2}y}{{\text{d}}x^{2}}}\right)}{\frac {{\text{d}}^{2}y}{{\text{d}}x^{2}}}}$.

积分后，我们有

$y=c^{2}{\frac {{\text{d}}^{2}y}{{\text{d}}x^{2}}}$

其中 $c^{2}$ 是积分常数。由于 $y=e^{\frac {x}{c}}$ 和 $y=e^{-{\frac {x}{c}}}$ 是这个微分方程的两个解，通解为

$y=c_{1}e^{\frac {x}{c}}+c_{2}e^{-{\frac {x}{c}}}$,

其中 $c_{1}$ 和 $c_{2}$ 是常数。这个最后一个方程是悬链线的方程。

第四条.
因此，借助极值理论，我们确实得到了某个结果；但另一方面，我们还需要问这个曲线是否真的给出了最小值；由于我们得出结论的方式，我们还需要看看这个曲线是否只是在某一段范围内或者在其整个范围内都具有问题中所要求的性质。

我们坚持最后陈述的合理性可以从下面的内容中看出，后面将证明上面找到的曲线仅在给定的范围内满足所要求的条件。

一个简单的考虑表明，我们上面所遵循的方法并不严谨；因为它预设了，这本身是不可接受的，即满足问题的曲线在其整个范围内都是规则的，否则，两点 $(x-\Delta x,y')$ 和 $(x,y)$ 之间的曲线部分不能用连接这两点的直线代替；同样，泰勒定理的展开也不允许。

第五条.
极值问题和变分法问题的本质区别在于，在第一种情况下，我们只需要处理有限个离散点，而在变分法中，问题涉及的是连续的一系列点。

如果我们希望用折线代替曲线，然后对折线应用类似于上面使用的那些方法，那么就会发现，在我们找到满足所有条件的折线之后，还需要证明从折线到曲线的必要极限转换实际上导致满足问题条件的确定曲线。

第六条.
任何极限转换，例如从多边形到曲线，如果我们使用积分的概念，它本身就会完成，因为积分表示无限多个数量的和的极限值，这些数量按照一定的规律增加，从而数量本身也相应地变小。

因此，如果我们用以下公式定义曲线 $y=f(x)$ 的表面积，我们需要找到这个面积，则

$S=2\pi \int y~{\text{d}}s$,

或者

${\frac {S}{2\pi }}=\int _{x_{0}}^{x_{1}}y{\sqrt {1+\left({\frac {{\text{d}}y}{{\text{d}}x}}\right)^{2}}}~{\text{d}}x$,

那么，对于在 $P_{0}$ 和 $P_{1}$ 之间绘制的每条曲线，此积分都将具有确定的值，因此问题可以表述如下。

问题 I. $y$ 应该如何确定为 $x$ 的函数，使得上述积分的值最小？

这个问题的解将在后面给出。上面给出的两种方法是为了说明最大值与最小值理论和变分法之间的共同点，以及它们之间的区别。

在微积分中，给出了一个确定的函数，并寻找变量或变量（如果有多个变量）的特定值，使得函数取最大值或最小值；在变分法中，寻找一个函数，并给出一个表达式，该表达式以某种已知的方式依赖于该函数。我们考虑一个确定的积分，其中被积函数以某种已知的方式依赖于未知函数，并要求未知函数必须具有什么形式，才能使确定积分取最大值或最小值。

我们只处理变量的实数值。

第七条.
如果 $t_{2}<t_{3}$ 且点 $P_{2}$ 对应于 $t_{2}$ 且 $P_{3}$ 对应于 $t_{3}$，则 $P_{3}$ 相对于 $P_{2}$ 被称为后点；而 $P_{2}$ 相对于 $P_{3}$ 被称为前点。

正如第 2 条所述，所需曲线的纵坐标 $y$ 是横坐标 $x$ 的单值函数。通常情况下，我们无法预先知道某个纵坐标是另一个纵坐标的单值函数。庞加莱 已经证明，当两个变量 $x$，$y$ 之间存在解析关系时，总是可以将这两个变量表示为第三个变量 $t$ 的单值函数。这个变量唯一需要的性质是，当它遍历两个给定极限之间的所有值时，对应的点 $(x,y)$ 沿着曲线从起点到终点遍历，并且对于更大的 $t$ 值，对应着曲线上更后面的点。

例如，假设 $z-x^{y}$，其中 $x$ 和 $y$ 是两个独立变量。那么，根据这个方程，没有办法在不引入超越函数的情况下表达这两个变量之间的依赖关系。但是，如果我们写

$x=e^{t}$

那么

$z=e^{yt}$

或者

$y={\frac {\log(z)}{t}}$

因此，$x$ 和 $y$ 是变量 $t$ 的单值函数。

如果我们在问题 I 的积分中引入这样一个新的变量 $t$，这个积分就变成了

${\frac {S}{2\pi }}=\int _{t_{0}}^{t_{1}}y{\sqrt {x'^{2}+y'^{2}}}~{\text{d}}t$,

我们用 $x'$ 和 $y'$ 表示量 ${\frac {{\text{d}}x}{{\text{d}}t}}$ 和 ${\frac {{\text{d}}x}{{\text{d}}t}}$.

现在我们可以将问题 I 表述如下

量 $x$ 和 $y$ 需要被确定为参数 $t$ 的单值函数，以使上述积分的值尽可能小。

第 8 条.
为了学习变分法的基本性质，我们将接下来制定其他简单的问题；然后，当我们寻求这些问题的普遍特征时，我们将会自然而然地得到变分法需要解决的问题的更精确的陈述。

作为第二个问题，可以给出变分法中非常著名的一个问题，即 *最速降线* (最快下降的曲线)，可以表述如下

问题 II. 两点 $A$ 和 $B$ 位于一个竖直平面内，点 $B$ 的位置低于点 $A$；需要在这两点之间画出一条曲线，使得一个在重力作用下并被限制在这条曲线上运动的质点，在给定的初速度下，从点 $A$ 运动到点 $B$ 所需的时间最短。

设质点的质量为1，其初速度为$\alpha$，重力加速度为$2g$，时间为$t$，点$A$和$B$的坐标分别为$(0,0)$和$(a,b)$。设正$Y$轴方向为下落物体（由于重力）的方向，设正$X$轴方向为点$B$所在的边。那么，根据能量守恒定律，

$\left({\frac {{\text{d}}x}{{\text{d}}t}}\right)^{2}+\left({\frac {{\text{d}}y}{{\text{d}}t}}\right)^{2}=4gy+\alpha ^{2}$,

或者

${\text{d}}t={\frac {\sqrt {{\text{d}}x^{2}+{\text{d}}y^{2}}}{\sqrt {4gy+\alpha ^{2}}}}={\frac {\sqrt {1+\left({\frac {{\text{d}}y}{{\text{d}}x}}\right)^{2}}}{\sqrt {4gy+\alpha ^{2}}}}~{\text{d}}y$;

因此

$T=\int _{0}^{b}{\frac {\sqrt {1+\left({\frac {{\text{d}}y}{{\text{d}}x}}\right)^{2}}}{\sqrt {4gy+\alpha ^{2}}}}~{\text{d}}y$.

我们的问题是：如何确定$x$关于$y$的函数，使得上述积分值最小？

关于上述积分中出现的根号的符号，很明显，这些符号在运动开始时必须相同，可以取正号。从力学角度来看，曲线在开始时必须下降；因此，在运动开始时，$y$ 随着 $t$ 的增加而增加，因此为正。由于 $4gy+\alpha ^{2}$ 始终为正量，等于 $\left({\frac {{\text{d}}x}{{\text{d}}t}}\right)^{2}+\left({\frac {{\text{d}}y}{{\text{d}}t}}\right)^{2}$，并且永远不会消失，我们总是可以给 ${\sqrt {4gy+\alpha ^{2}}}$ 正号。同样，在运动开始时，量 ${\sqrt {1+\left({\frac {{\text{d}}y}{{\text{d}}x}}\right)^{2}}}$ 必须取正号，因为 ${\text{d}}t$ 始终代表时间的正增量。然而，在运动的后续过程中，可能会发生 ${\text{d}}y=0$。那么量 ${\sqrt {1+\left({\frac {{\text{d}}y}{{\text{d}}x}}\right)^{2}}}$ 会趋于无穷大，使得 ${\text{d}}y$ 和 ${\sqrt {1+\left({\frac {{\text{d}}y}{{\text{d}}x}}\right)^{2}}}$ 可以同时改变它们的符号，而 ${\sqrt {4gy+\alpha ^{2}}}$ 继续保持正号。

第 9 条.
问题陈述中假设 $B$ 必须位于 $A$ 下方，这一点并不重要。因为质点在 $B$ 具有特定的速度 $\beta$，我们可以根据初始速度 $\alpha$ 和 $A$ 相对于 $B$ 的高度计算出来。当质点以该速度到达 $B$ 时，它可以再次上升，当它到达 $B$ 另一侧的高度 $A$ 时，它将具有初始速度。如果我们假设上升所经过的曲线与下降所经过的曲线对称，那么上升所需的时间与下降所需的时间相同。

因此，如果质点从 $B$ 开始运动，我们可以根据 $\beta$（现在是初始速度）计算出点 $A$ 的速度 $\alpha$。如果我们寻找的是初始速度为 $\beta$ 的质点在最短时间内到达 $A$ 所经过的曲线，那么我们就得到了问题的答案。

就当前问题而言，从物理角度来看，我们看到$y$ 是 $x$ 的单值函数。由于这在所有情况下都不可能，因此方便起见，此处也用两个方程表示曲线；也就是说，将 $x$ 和 $t$ 视为第三个变量 $t$ 的单值函数，其中 $t$ 仅受一个条件的约束，即当它遍历两个给定极限之间的所有值时，相应的点 $x$，$y$ 沿着曲线从起点移动到终点，并且以这样一种方式，即 $t$ 的更大值对应于曲线上较后的点。

上述积分变为

$T=\int _{t_{0}}^{t_{1}}{\frac {\sqrt {x'^{2}+y'^{2}}}{\sqrt {4gy+\alpha ^{2}}}}~{\text{d}}t$,

其中我们用 $x'$ 和 $y'$ 分别表示 ${\frac {{\text{d}}x}{{\text{d}}t}}$ 和 ${\frac {{\text{d}}y}{{\text{d}}t}}$。

那么，我们的问题是：*确定 $x$ 和 $y$ 作为参数 $t$ 的函数，使刚刚写出的积分具有尽可能小的值。*

第 10 条.
问题 III。*在规则曲面 $f(x,y,z)=0$ 上的两点之间，需要绘制一条曲线，使它的长度最小。*

考虑一个表面，它可以用两个参数 $u$ 和 $v$ 的单值正则函数 表示的正交坐标 $x$，$y$，$z$。如果我们把这些坐标看作平面上一个点的直角坐标，那么表面上的每个点都将对应于 $uv$ 平面上一个确定的点，而这些点集合起来将在平面上构成一个确定的区域，可以把它看作是表面在平面上的投影。表面上的每一条曲线在这个 $uv$ 平面的区域中都对应一条曲线，反之亦然。

此外，把 $u$ 和 $v$ 看作一个量 $t$ 的单值函数；因此，对于每个 $t$ 值，都对应于 $uv$ 平面上一个点，因此，如果这个点位于 $uv$ 平面的确定区域中，那么它对应于表面上一个确定的点。

因此，如果 $t_{0}$ 和 $t_{1}$ 是对应于表面上两个固定点的 $t$ 值，那么在这两个点之间任何曲线的长度可以通过以下公式确定：

$L=\int _{t_{0}}^{t_{1}}{\sqrt {P\left({\frac {{\text{d}}u}{{\text{d}}t}}\right)^{2}+2Q{\frac {{\text{d}}u}{{\text{d}}t}}\cdot {\frac {{\text{d}}v}{{\text{d}}t}}+R\left({\frac {{\text{d}}v}{{\text{d}}t}}\right)^{2}}}~{\text{d}}t$,

其中

$P=\left({\frac {\partial x}{\partial u}}\right)^{2}+\left({\frac {\partial y}{\partial u}}\right)^{2}+\left({\frac {\partial z}{\partial u}}\right)^{2}$,

$Q={\frac {\partial x}{\partial u}}{\frac {\partial x}{\partial v}}+{\frac {\partial y}{\partial u}}{\frac {\partial y}{\partial v}}+{\frac {\partial z}{\partial u}}{\frac {\partial z}{\partial v}}$,

$R=\left({\frac {\partial x}{\partial v}}\right)^{2}+\left({\frac {\partial y}{\partial v}}\right)^{2}+\left({\frac {\partial z}{\partial v}}\right)^{2}$.

然后，我们要确定 $u$ 和 $v$ 作为 $t$ 的函数，使得 $L$ 为最小值。

第11条.
对于上述问题，需要应用此处给出的表示方法，而在问题 I 和问题 II 中，将$x$ 和 $y$ 表达为 $t$ 的单值函数可以被认为是方便的。在问题 III 中，变量 $u$ 和 $v$ 必须被认为是第三个变量的函数。我们不能将 $v$ 视为 $u$ 的函数，因为我们对曲线的轨迹一无所知。如果我们想将 $v$ 仅仅视为 $u$ 的双值函数，我们仍然会遇到许多困难。因此，必须要求 $u$ 和 $v$ 被确定为 $t$ 的单值函数，使得上一篇文章中的积分取最小值。

第 12 条.
问题 IV. 求旋转曲面的形状，该曲面绕一个固定方向的轴旋转，并在液体中沿轴方向运动时阻力最小，假设曲面元素的阻力与其法线方向的速度分量的平方成正比。

这个问题是牛顿提出的。

假设可以忽略物体与流体之间的摩擦以及流体内部的摩擦。

令 $Y$ 轴为旋转轴，${\text{d}}s$ 为母线的元素，$\theta$ 为法线与 $Y$ 轴之间的夹角，使得 ${\frac {{\text{d}}x}{{\text{d}}s}}=\cos(\theta )$。

因此，曲面的一段区域由下式给出

$2\pi x{\text{d}}s={\sqrt {2\pi x{\sqrt {x'^{2}+y'^{2}}}}}~{\text{d}}t$.

法线方向的速度分量为 $v\cos(\theta )$，该区域在法线方向的阻力为

$v^{2}\cos ^{2}(\theta )2\pi x{\sqrt {x'^{2}+y'^{2}}}~{\text{d}}t$.

将这个数量乘以 $\cos(\theta )$，即可得到沿 $Y$ 轴方向的阻力。因此，我们可以用积分来表示物体的所需阻力。

${\frac {R}{2\pi v^{2}}}=\int {\frac {xx'^{3}}{x'^{2}+y'^{2}}}~{\text{d}}t$.

我们的问题是，用一条曲线连接两点 $P_{1}$ 和 $P_{2}$，使得它绕 $Y$ 轴旋转产生的区域阻力最小。忽略常数因子 ${\displaystyle }$2\pi v^{2}，我们需要确定 $x$ 和 $y$ 作为 $t$ 的单值函数，使得积分

$R=\int {\frac {xx'^{3}}{x'^{2}+y'^{2}}}~{\text{d}}t$

为最小值。

第 13 条.
上述四个问题的共同点在于确定 $x$ 和 $y$ 作为量 $t$ 的单值函数，使得一个依赖于它们的积分形式为

$I=\int _{t_{0}}^{t_{1}}F(x,y,x',y')~{\text{d}}t$

将具有最小可能的值。这里$t_{0}$ 和 $t_{1}$ 具有固定值，使得相应的坐标 $x$，$t$ 曲线的起点和终点应该是已知的。

$F(x,y,x',y')$ 表示四个参数 $x$，$t$，$x'$，$y'$ 的单值正则函数，其中 $x'$ 和 $y'$（因为它们代表曲线的切线方向）被认为是无限制的，而点 $x$，$y$ 的区域可能是整个平面，也可能只是它的一个连续部分。

第十四条.
条件$t_{0}$，$t_{1}$ 应该具有固定值并不重要；此外，两个端点都可以移动，就像第三个问题的例子，如果我们给它以下形式： *在曲面上给定两条曲线；在一条曲线上的点和另一条曲线上的点之间所有可能的曲线中，找到长度最短的曲线。* 我们习惯称之为两条曲线的测地距离。

为了解决这个问题，我们必须首先解决特殊的第三问题，因为，如果一条曲线具有如上所述的最小长度的属性，那么当我们将端点固定时，它也必须保留相同的属性。因此，从 III 中可以确定曲线的性质。端点的变化此外还给出了一些曲线必须具有的特殊属性。

例如，位于同一平面上的两条曲线之间的最短距离显然是一条直线；通过端点的变化，可以得出这条直线必须同时垂直于两条曲线。

第十五条.
与前面给出的四个问题本质上不同的问题是以下问题

第五问题。*需要绘制一条闭合曲线，该曲线在给定周长的情况下，能够包含最大的面积。*

令 $x$ 和 $y$ 是 $t$ 的单值函数，例如 $x(t)$ 和 $y(t)$，使得对于 $t$ 的两个确定值 $t_{0}$ 和 $t_{1}$，曲线上的对应点 $x$，$y$ 重合，并且如果 $t$ 从较小的值 $t_{0}$ 增加到较大的值 $t_{1}$，点 $x$，$y$ 沿着正方向完全遍历了曲线。那么曲线所包含的曲面的两倍面积由积分表示为

$I^{(0)}=\int _{t_{0}}^{t_{1}}(xy'-yx')~{\text{d}}t$,

而曲线的周长由积分给出

$I^{(1)}=\int _{t_{0}}^{t_{1}}{\sqrt {x'^{2}+y'^{2}}}~{\text{d}}t$.

那么，我们的问题是：*确定$x$和$y$作为$t$的单值函数，使得$I^{(0)}$的值最大，同时$I^{(1)}$具有给定的值。*

第16条.
问题VI：*一根无限薄、绝对柔韧但不可伸展的线段，两端固定，在仅受重力作用下，会呈现什么样的形状？*

这个问题具有最小值的特点，因为在稳定平衡状态下，重心必须尽可能低。如果将$Y$-轴取为竖直向上方向，并且如果用$S$表示曲线的长度，并且用$\xi$，$\eta$表示重心的坐标，则$\eta$由以下方程确定

$\eta S=\int _{t_{0}}^{t_{1}}y{\sqrt {x'^{2}+y'^{2}}}~{\text{d}}t$,

其中

$S=\int _{t_{0}}^{t_{1}}{\sqrt {x'^{2}+y'^{2}}}~{\text{d}}t$.

这个问题可以表述为：*变量${\displaystyle }$和${\displaystyle }$需要被确定为一个量$t$的单值函数，以使上述第一个积分取最小值，同时第二个积分保持一个给定的固定值。*

第17条.
问题 V 和 VI 通常归类为 _相对极大值和极小值_，这个术语不需要进一步解释。一般来说，它们包含在以下问题中：_令 $F^{(0)}(x,y,x',y')$ 和 $F^{(1)}(x,y,x',y')$ 是与第 13 节中函数 $F(x,y,x',y')$ 同一性质的两个函数。要求确定 $x$ 和 $y$ 为数量 $t$ 的单值函数，使得积分_

$I^{(0)}=\int _{t_{0}}^{t_{1}}F^{(0)}(x,y,x',y')~{\text{d}}t$

具有极大值或极小值，同时积分_

$I^{(1)}=\int _{t_{0}}^{t_{1}}F^{(1)}(x,y,x',y')~{\text{d}}t$

保持给定的值。

第 18 节.
在下文中，我们将给出我们认为是对已提出的问题的严格处理。读者可以为自己提出自然扩展；例如，不是取两个变量，而是考虑一个以 $n$ 个变量的函数作为被积函数的积分。此外，将这些变量置于辅助条件下，并允许变量相对于数量 $t$ 的二阶和更高阶导数进入讨论。然后，导致极小曲面研究的二重积分可以通过变分方法处理（参见第 175 节以下）。

第 19 节.
我们可以通过引入一个基本概念 _曲线变分的概念_，以更普遍的方式定义变分法的对象。在过去，变分法被认为是分析中最难的分支之一。人们错误地认为，困难在于基本概念（尤其是曲线变分概念）的缺乏清晰度。出现的困难大多是其他方面的。

在极大值和极小值理论中，我们说，对于变量的某个确定值系统，如果该函数对于该值系统的值大于或小于它对于所有相邻值系统的值，则该函数的值是极大值或极小值。

我们说^[6]一个变量的函数 $f(x)$ 在某个确定位置 $x=a$ 有一个最大值或最小值，如果这个值对于 $x=a$ 分别大于或小于 $x$ 的所有其他值，这些值位于 $|x-a|<\delta$ 的邻域内，并且这个邻域我们可以无限接近 $a$。

分析条件是 $f(x)$ 在位置 $x=a$

最大值，用 $f(x)-f(a)<0$ 表示，对于 $|x-a|<\delta$

最小值，用 $f(x)-f(a)>0$ 表示，对于 $|x-a|<\delta$

同样，我们说一个 $n$ 个变量的函数 $f(x_{1},x_{2},\ldots ,x_{n})$ 在某个确定位置 $x_{1}=a_{1},x_{2}=a_{2},\ldots ,x_{n}=a_{n}$ 有一个最大值或最小值，如果这个值对于 $x_{1}=a_{1},x_{2}=a_{2},\ldots ,x_{n}=a_{n}$ 分别大于或小于所有其他位于邻域 $|x_{\lambda }-a_{\lambda }|<\delta _{\lambda }~(\lambda -1,2,\ldots ,n)$ 内的值，并且这个邻域我们可以无限接近第一个位置。

就像我们在这里谈论的是一个相邻的值系统，同样我们在变分法中谈论的是位于给定曲线邻域内的曲线。我们要求在最小值情况下，积分在给定曲线上取值应该小于，而在最大值情况下，积分在给定曲线上取值应该大于在任何相邻曲线上的取值。

为了确定相邻曲线的概念，并使之与相邻值系的观念类比清晰，让我们首先考虑一条折线 A-$A_{1}A_{2}A_{3}\ldots A_{n}$，而不是给定的曲线，并让它从其原始位置稍微滑动。

然后在新位置，每个角点 $B_{k}$ 将对应于旧位置中的一个确定角点 $A_{k}$，而且新位置 $B_{1}B_{2}B_{3}\ldots B_{n}$ 将与旧位置 $A_{1}A_{2}A_{3}\ldots A_{n}$ 的差异尽可能小，如果我们规定任何两个对应点 $A_{k}$ 和 $V_{k}$ 之间的距离应小于任何数量 $\delta$，其中 $\delta$ 尽可能小。现在，通过增加边数，让折线过渡到给定的曲线；然后，点 $B_{1}B_{2}B_{3}\ldots B_{n}$ 也会形成一条曲线，它与第一条曲线相差很小，因此我们称之为第一条曲线的 *相邻曲线*。

因此，我们可以说一条曲线 *与* 另一条曲线 *相邻*，或者通过一个 *变化* 从另一条曲线中产生，这个变化可以任意小，如果后一条曲线上的每个点都对应于前一条曲线上的一个确定点，而且任何两个对应点之间的距离都小于 $\delta$，其中 $\delta$ 可以任意小。

相邻曲线的几何概念并不模糊。同样，很容易看出，对于曲线的每一个变化，积分

$\int F(x,y,x',y')~{\text{d}}t$,

也会发生相应的变化，当第二条曲线与第一条曲线相邻时，这种变化将无限小。

当然，如果积分要取最大值，那么积分值的这种变化必须是 *连续的、负的*；如果积分要取最小值，那么积分值的这种变化必须是 *连续的、正的*。

第 20 条.
观察上面所说，我们可以将第 13 和 17 条的问题表述如下

变量 $x$ 和 $y$ 应被确定为量 $t$ 的单值函数，以使当我们用方程 $x=x(t)$，$y=y(t)$ 定义曲线时，并使曲线尽可能地发生变化，积分中产生的变化

$I=\int _{t_{0}}^{t_{1}}F(x,y,x',y')~{\text{d}}t$

必须是连续正数，如果要进入最小值，并且是连续负数，如果我们要求最大值。

在相对极大值和极小值的情况下，对于曲线的任何无限小的变化，积分

$I^{(1)}=\int _{t_{0}}^{t_{1}}F^{(1)}(x,y,x',y')~{\text{d}}t$

保持其值不变，积分

$I^{(0)}=\int _{t_{0}}^{t_{1}}F^{(0)}(x,y,x',y')~{\text{d}}t$

根据是出现最大值还是最小值，必须始终小于或始终大于由方程 $x=x(t)$，$y=y(t)$ 给出的曲线。

第 21 条.
我们必须寻求严格的方法来解决上述问题。雅可比和较早的数学家，伯努利及其同时代，牛顿和莱布尼茨所采用的解决这些问题的方法，仅仅导致了某些微分方程的形成，在有利的情况下，导致了这些方程的积分。但这些方法不足以确定性地确定所找到的曲线实际上是否具有所要求的性质。

我们知道，在普通极大值和极小值理论的问题中，并不总是需要存在极大值或极小值 肯定的是，任何变量在一个变量有意义的区域内都有一个上限和一个下限。因此，存在一个极限 $l$ 使得变量可以取的所有值都大于 $l$，并且在 $l$ 的邻域中，变量都可以取值。我们将 $l$ 称为变量的下限。同样，也存在一个上限。这些极限并不总是能达到。因此，有两种情况可能发生：变量可以实际上达到表示为上限和下限的值，或者变量只能无限接近而永远无法达到这些极限。因此，假设存在极大值或极小值是不可取的。例如，上面提到的牛顿问题没有解，在第一个问题中，有时存在最小值，有时不存在最小值。

问题.

建议学生选择以下两个或三个问题，并采用与对已提出的六个问题所做相同的解题方法。

1. 最小作用原理。求积分

$u=\int {\sqrt {(x+a)(1+p^{2})}}~{\text{d}}x$

当$x$ 和 $p={\frac {{\text{d}}y}{{\text{d}}x}}$ 的极限值固定，并确定在什么条件下，抛物线实际上是该问题的解。这个问题也可以这样表述：确定一个粒子的路径，使得其作用 $\int v{\text{d}}s$ 在固定点之间最小，如果粒子在任何一点的速度 $v$ 是由于从直线 $x+a=0$（$X$ 轴垂直向下）自由下落产生的。[见 Todhunter，变分法的研究，第 147 页；另见数学季刊，1868 年 11 月] 这里的不连续性与我们在问题 I（第 1 页）中发现的不连续性非常相似。

2. 行星椭圆运动的最小作用原理。一个粒子从给定点以给定速度被发射，并受到固定点的吸引，吸引力与距离的平方成反比。确定到第二个固定点的最小作用路径。[见 Todhunter，研究等，第 160 页；Todhunter，变分法的历史，第 251 页；Jellett，变分法，第 76 页；Jacobi，Crelle，第 17 卷，第 68 页；Liouville 的期刊，第三卷，第 44 页；Delaunay，Liouville 的期刊，第六卷，第 209 页。]

3. 确定使积分 $u=\int yx{\text{d}}x$ 达到最大值的曲线，其中变量的极限值已固定。[见 欧拉，求解最大最小线的方法，洛桑，1794，第 52 页；Woodhouse，等周问题与变分法的论述，第 124 页。]

4. 给定曲线的长度，确定其性质，当它绕固定轴旋转产生的体积最大或最小。[见 欧拉，方法等，第 196 页；Woodhouse，论述等，第 125 页；Moigno et Lindelof，变分法，第 216 页；Jellett，变分法，第 160 页。]

5. 求绕固定轴旋转时产生最大或最小体积的曲线，曲面的面积保持不变。[见 欧拉，方法等，第 194 页；Moigno et Lindelof，变分法，第 218 页；Delaunay，Liouville 的期刊，第六卷，第 315 页；哲学杂志，1866 年；Todhunter，研究等，第 68 页；Jellett，变分法，第 161 页及注释，第 364 页。]

6. 找到绕轴旋转时生成最大体积固体的曲线，曲线的长度和面积都已知。[见 Lacroix，微分积分，第二卷，第 713 页；另请参阅上述参考文献以了解此问题和后续问题。]

7. 找到当曲线长度已知时的最速降曲线。[见 约翰·伯努利著作，第二卷，第 255 页；巴黎科学院回忆录，1718 年，第 120 页。]

8. 给定平面曲线，确定第二条长度已知的曲线，使得两条曲线之间包围的面积最大。

9. 在所有长度相同的曲线中，找到一条曲线，使其绕轴旋转时生成最大或最小的表面积。

10. 求最大或最小化积分

$u=\int _{x_{0}}^{x_{1}}\phi (x,y,z){\sqrt {1+y'^{2}+z'^{2}}}~{\text{d}}x$,

其中 $\phi$ 是变量 $x$、$y$、$z$ 的已知函数，它们由方程 $f(x,y,z)=0$ 联系，$f$ 是已知函数。

11. 找到空间中两固定点之间长度最短的曲线，曲率半径为常数。

12. 找到给定体积的均匀物体必须采取的形式，使其对一个特定方向上的物质点的吸引力最大。