变分法/第六章

第六章：微分方程 $G=0$ 的解的形式。

• 87 微分方程 $G=0$ 的另一种形式。
• 88 函数 $F_{1}$ 的另一种形式。
• 89 幂级数积分。
• 90 微分方程 $G=0$ 的解 $x=\phi (t,\alpha ,\beta )$，$y=\psi (t,\alpha ,\beta )$。
• 91，92 当 $F_{1}=0$ 在曲线的初始点时。
• 93 当 $s$ 是自变量时，微分方程 $G=0$ 的形式。
• 94 该方程的解。
• 95 曲线在所讨论的区间内不能有奇点。曲线中任意点的坐标用 $s$ 的幂级数表示。

第 87 条.
在我们继续研究积分

$I=\int _{t_{0}}^{t_{1}}F(x,y,x',y')~{\text{d}}t{\text{,}}\qquad {\text{[1]}}$

的最大值或最小值存在的进一步条件之前，我们将努力更仔细地研究微分方程 $G=0$ 的性质和形式。

我们假设满足微分方程

$G={\frac {\partial ^{2}F}{\partial x\partial y'}}-{\frac {\partial ^{2}F}{\partial y\partial x'}}+F_{1}\left(x'{\frac {{\text{d}}y'}{{\text{d}}t}}-y'{\frac {{\text{d}}x'}{{\text{d}}t}}\right)=0{\text{,}}\qquad {\text{[2]}}$

已知曲线 $F_{1}$ 不等于零，设 $A$ 为曲线的起点，$AA'$ 为曲线在 $A$ 处的方向。假设微分方程 $G=0$ 具有最简单的形式，如果我们把其中一个坐标视为另一个坐标的单值函数。在上述积分 $I$ 中，量 $x$，$y$ 对量 $t$ 的依赖性仅受一个条件的限制，即当 $t$ 从 $t_{0}$ 连续递增到 $t_{1}$ 时，点从起点移动到终点。

我们可以用无限多种方式在 $t$ 的位置引入另一个变量 $\tau$，其中

$t=f(\tau )$

只需要函数 $f$ 的形式满足以下条件：随着 $\tau$ 的增加，$\tau$ 也随之增加。我们可以反过来用

$\tau =\phi (t)$.

再次引入 $\tau$。积分 $I$ 和微分方程 $G=0$ 的形式在这些变换下不会改变。

在某些情况下，我们可以选择将 $t$ 坐标 $x$ 本身作为自变量，这种情况发生在沿着曲线从起点到终点移动时，x 连续增加。特别地，我们可以将 $X$-轴作为起点 $A$ 的切线，并将曲线的走向作为 $X$-轴的正方向。由于我们只考虑正则曲线或由正则部分组成的曲线，因此如果点 $P$ 从点 $A$ 开始沿着曲线移动，它到 $A$ 处的法线的距离在曲线的某个部分连续增加。因此，对于这部分曲线，如果我们将 ${\displaystyle }$ 处的法线的正方向作为正 $Y$-轴，则对于每个 $x$ 值，只有一个 $y$ 值。因此，对于曲线的特定部分，我们可以始终假设，通过适当选择坐标系，第二个坐标可以看作是第一个坐标的单值函数。因此，我们只需要进行坐标变换。

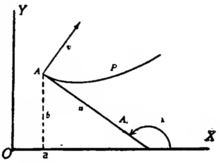
令新坐标原点的坐标为 $a$，$b$，并且令

$x=a+gu+g'v$，$y=b+hu+h'v$，$\qquad {\text{[3]}}$

其中 $u$ 和 $v$ 是新的坐标。

如果 $\lambda$ 是 $X$ 轴和 $u$ 轴之间的夹角，那么我们有众所周知的公式

$g=\cos(\lambda )$，$h=\sin(\lambda )$，$g'=-\sin(\lambda )$，$h'=\cos(\lambda )$。 $\qquad {\text{[4]}}$

积分 $I$ 然后变为，因为 $u$ 可以被看作是独立变量，

$I=\int _{0}^{u}F\left(a+gu+g'v,b+hu+h'v,g+g'{\frac {{\text{d}}v}{{\text{d}}u'}},h+h'{\frac {{\text{d}}v}{{\text{d}}u}}\right)~{\text{d}}u$,

为了简洁，我们将其表示为

$I=\int _{0}^{u}f\left(u,v,{\frac {{\text{d}}v}{{\text{d}}u}}\right)~{\text{d}}u$。 $\qquad {\text{[5]}}$

如果我们进一步写出 ${\frac {{\text{d}}v}{{\text{d}}u}}=v'$ 那么 [5] 变为

$I=\int _{0}^{u}f(u,v,v')~{\text{d}}u$。 $\qquad {\text{[}}5^{\text{a}}{\text{]}}$

如果我们将上一章第 74-80 节中使用的方法应用于此积分，我们将得到一个微分方程来确定 $v$ 作为 $u$ 的函数。

设曲线仅沿纵坐标方向滑动 $v$，因此将 $v+{\bar {v}}$ 代替 $v$，其中 ${\bar {v}}$ 是一个非常小的量，在所考虑曲线段的端点和起点处消失。进行变分的积分是

$I+\Delta I=\int f\left(u,v+{\bar {v}},v'+{\frac {{\text{d}}{\bar {v}}}{{\text{d}}u}}\right)~{\text{d}}u$.

接下来，我们根据 ${\bar {v}}$ 和 ${\frac {{\text{d}}{\bar {v}}}{{\text{d}}u}}$ 的幂展开 $\Delta I$。一阶项的总和为

$\delta I=\int _{0}^{u}\left({\frac {\partial f}{\partial v}}{\bar {v}}+{\frac {\partial f}{\partial v'}}{\frac {{\text{d}}{\bar {v}}}{{\text{d}}u}}\right)~{\text{d}}u{\text{,}}\qquad {\text{[6]}}$

或者，因为

${\frac {\partial f}{\partial v'}}{\frac {{\text{d}}{\bar {v}}}{{\text{d}}u}}={\frac {\text{d}}{{\text{d}}u}}\left({\bar {v}}{\frac {\partial f}{\partial v'}}\right)-{\bar {v}}{\frac {\text{d}}{{\text{d}}u}}{\frac {\partial f}{\partial v'}}$,

我们有

$\delta I=\int _{0}^{u}\left({\frac {\partial f}{\partial v}}-{\frac {\text{d}}{{\text{d}}u}}{\frac {\partial f}{\partial v'}}\right){\bar {v}}~{\text{d}}u+\left[{\bar {v}}{\frac {{\text{d}}f}{{\text{d}}v'}}\right]_{0}^{u}$. $\qquad {\text{[6}}^{a}{\text{]}}$

方括号内的量为零，因为 ${\bar {v}}=0$ 在极限情况下。此外，我们必须有

$\delta I=0$.

由于 ${\bar {v}}$ 是任意的，仅受必须在极限处消失的条件约束，从上一章的引理可知

${\frac {\text{d}}{{\text{d}}u}}{\frac {\partial f}{\partial v'}}-{\frac {\partial f}{\partial v}}=0$,

或者

${\frac {\partial ^{2}f}{\partial ^{2}v'^{2}}}{\frac {{\text{d}}v'}{{\text{d}}u}}+{\frac {\partial ^{2}f}{\partial v\partial v'}}v'+{\frac {\partial ^{2}f}{\partial u\partial v'}}-{\frac {\partial f}{\partial v}}=0$. $\qquad {\text{[2}}^{a}{\text{]}}$

第 88 条.
如果一个坐标可以被认为是另一个坐标的单值函数，则方程 [$2^{\text{a}}$] 可以代替形式 [2] 用于 $G=0$.

现在我们将证明在 [$2^{\text{a}}$] 中出现的量 ${\frac {\partial ^{2}f}{\partial v'^{2}}}$ 与 $F_{1}$ 相同，前提是在函数 $F(x,y,x',y')$ 中 $x$ 和 $y$ 可以被视为仅是 $u$ 的函数。

因为

$f(u,v,v')\equiv F(a+gu+g'v,b+hu+h'v,g+g'v',h+h'v')\equiv F(x,y,x',y')$,

因此，我们得到

${\frac {\partial f}{\partial v'}}={\frac {\partial F}{\partial x'}}g'+{\frac {\partial F}{\partial y'}}h'$,

因此

${\frac {\partial ^{2}f}{\partial v'^{2}}}={\frac {\partial ^{2}F}{\partial x'^{2}}}g'^{2}+2{\frac {\partial ^{2}F}{\partial x'\partial y'}}g'h'+{\frac {\partial ^{2}F}{\partial y'^{2}}}h'^{2}$.

另一方面，根据其定义，$F_{1}$ 由以下任一关系确定： 

${\frac {\partial ^{2}F}{\partial x'^{2}}}=F_{1}y'^{2}$; ${\frac {\partial ^{2}F}{\partial x'}}{\partial y'}=-F_{1}x'y'$; ${\frac {\partial ^{2}F}{\partial y'^{2}}}=F_{1}x'^{2}$. $\qquad {\text{[7]}}$

由此可知

${\frac {\partial ^{2}f}{\partial v'^{2}}}=(g'^{2}y'^{2}-2g'h'x'y'+h'^{2}x'^{2})F_{1}=(g'y'-h'x')^{2}F_{1}=(g'h-h'g)^{2}F_{1}=(-\sin ^{2}(\lambda )-\cos ^{2}(\lambda ))^{2}F_{1}$;

或者最终，

${\frac {\partial ^{2}f}{\partial v'^{2}}}=F_{1}$. $\qquad {\text{[8]}}$

因此，[$2^{\text{a}}$] 可以写成

$F_{1}{\frac {{\text{d}}v'}{{\text{d}}u}}+{\frac {\partial ^{2}f}{\partial v\partial v'}}v'+{\frac {\partial ^{2}f}{\partial u\partial v'}}-{\frac {\partial f}{\partial v}}=0$.

因为我们有

$v'={\frac {{\text{d}}v}{{\text{d}}u}}$,

以及

$f(u,v,v')\equiv F(x,y,x',y')$,

其中 $x$，$y$ 由 $u$，$v$ 根据 [3] 确定，可以得出

$F_{1}{\frac {{\text{d}}^{2}v}{{\text{d}}u^{2}}}+{\frac {\partial ^{2}F}{\partial v\partial v'}}{\frac {{\text{d}}v}{{\text{d}}u}}+{\frac {\partial ^{2}F}{\partial u\partial v'}}-{\frac {\partial F}{\partial v}}=0$. $\qquad {\text{[2}}^{\text{b}}{\text{]}}$

第 89 条.
在微分方程理论中，已知任何形式为 [$2^{\text{b}}$] 的微分方程都可以用独立变量 $u$ 的幂级数形式进行积分。

作为一个特例，我们有以下情况：

假设 1) *要形成的幂级数所代表的曲线在初始点处，我们有*

$u=0$，$v=b_{0}$，

其中 $b_{0}$ 是一个任意常数；

2) 曲线在初始点的方向由任意常数确定

${\frac {{\text{d}}v}{{\text{d}}u}}=v_{0}'$;

那么，当 $u$ 的值足够小时，$v$ 可以用幂级数表示。

$v=b_{0}+v_{0}'u+\cdots$, $\qquad {\text{[9]}}$

我们假设 $F_{1}$ 在初始点 $(0,b_{0})$ 不为零。

$v$ 在位置 $(0,b_{0},v_{0}')$ 的二阶及更高阶导数都可以从微分方程 [$2^{\text{b}}$] 推导出来。因此，在 [9] 中，我们有 $v$ 是一个关于 $u$ 的幂级数，其系数除了每个问题中所含的常数外，还包含两个任意常数 $b_{0}$ 和 $v_{0}'$，它们在不同的曲线之间会发生变化。

第 90 条.
如果将方程 [9] 中给出的 $v$ 的表达式代入公式 [3]，我们有 $x$ 和 $y$ 用 $u$ 表示。在这些表达式中，出现了常数 $g$，$g'$，$h$，$h'$，它们依赖于 $u$ 以及 $u$，$v$ 坐标系的原点坐标 $a$，$b$ 以及两个积分常数 $b_{0}$ 和 $v_{0}'$，在第 89 条中定义。后两个常数在不同的曲线之间是不同的。在这些公式中，就像在第 89 条中一样，我们只能将小值赋给 $u$。

然而，我们知道，正如函数论中所看到的那样，如果一条曲线只在很小的一部分被给出，那么它的延续就被完全确定了。因此，我们只需要知道曲线在无限小的 $u$ 中的轨迹，就能随意跟踪它的轨迹。

曲线的坐标 $x$，$y$ 可以表示为 $t$ 和两个任意常数 $\alpha$ 和 $\beta$ 的函数。代替 $u$，我们可以引入另一个量的一个任意函数，只要这个量在曲线从起点到终点遍历时以连续方式增加。正如已经提到的，积分的两个常数在不同的曲线之间变化。如果我们适当地确定这些常数，我们可以迫使满足微分方程 $G=0$ 的曲线通过两个指定的点。

通过这种方式，我们清楚地了解了给出 $x$ 和 $y$ 的解析表达式的推导方式；一般来说，从方程 $G=0$ 中可以找到 $x$ 和 $y$，形式如下：

$x=\phi (t,\alpha ,\beta )$，$y=\psi (t,\alpha ,\beta )$。 $\qquad {\text{[10]}}$

同时可以看到，至少在一定程度上，$x$ 和 $y$ 是 $t$ 和两个积分常数 $\alpha$ 和 $\beta$ 的单值正则函数，因此最终我们也可以对这两个常数进行微分。

第 91 条.
在与第 89、90 条中所述内容相关的方面，这里似乎需要考虑一个例外情况，即 $G=0$ 中的例外情况，即：

${\frac {\partial ^{2}f}{\partial v'^{2}}}=F_{1}={\frac {\partial ^{2}F}{\partial x'^{2}}}\sin ^{2}(\lambda )-2{\frac {\partial ^{2}f}{\partial x'\partial y'}}\sin(\lambda )\cos(\lambda )+{\frac {\partial ^{2}F}{\partial y'^{2}}}\cos ^{2}(\lambda )\qquad {\text{[8]}}$

等于曲线原点 $(y=0,v-b_{0})$ 为零，该曲线满足方程 $G=0$.

我们将看到这只是一个特例，通过证明以下内容：

如果我们在点 $(u=0,v=b_{0})$ 周围画一个小圆，那么这个圆可以被分成若干扇形，使得在每个扇形内 ${\frac {\partial ^{2}f}{\partial v'^{2}}}$ 不等于零。因为我们可以把围绕初始点 $(u=0,v=b_{0})$ 的足够小的圆的半径视为该曲线的初始方向。如果对于 $v$ 我们在 [8] 中写出 [9] 中给出的幂级数，我们有，通过置 $F_{1}=0$，一个用来确定 $v_{0}'$ 的方程，也就是固定初始方向的量。这个方程要么没有实根，那么将不存在从点 $(u=0,v-b_{0})$ 出发的曲线，要么 $F_{1}$ 对于单个 $v_{0}'$ 消失，那么半径确定了不同的扇形。在这些扇形内，可以从点 $(u=0,v-b_{0})$ 沿各个方向画出曲线，其中 $F_{1}$ 不为零。因此，人们总是可以为 $v_{0}'$ 指定限制，在这些限制内，满足方程 $G=0$ 并从点 $(u=0,v-b_{0})$ 出发的曲线，在原点至少有一个 $F_{1}$ 不为零。

第 92 条.
最后我们将证明，从同一点 $(u=0,v-b_{0})$ 出发的，满足方程 $G=0$ 的曲线，在其初始点完全彼此分离。

如果我们在点 $(u=0,v=b_{0})$ 周围画一个小圆，那么在其边缘上，我们就可以很容易地确定点 $u$，$v$，它被其中一条曲线所截。假设 $\rho$ 是小圆的半径，那么

$u^{2}+(v-b_{0})^{2}=\rho ^{2}$。 $\qquad {\text{[11]}}$

将 [9] 中的幂级数代入 $v$，我们得到

$\rho ^{2}=(1+v_{0}'^{2})u^{2}+C_{3}u^{3}+\cdots$,

或者

$\rho ={\sqrt {1+v_{0}'^{2}}}u+(u)_{2}+\cdots$.

我们可以将这个级数反转，得到 $u$ 作为 $\rho$ 的函数，因此

$u={\frac {1}{\sqrt {1+v_{0}'^{2}}}}\rho +(\rho )_{2}'+\cdots \qquad {\text{[12.1]}}$

因此

$v-b_{0}={\frac {v_{0}'}{\sqrt {1+v_{0}'^{2}}}}\rho +(\rho )_{2}''+\cdots \qquad {\text{[12.2]}}$

这些级数对于所有在一定极限$\rho _{0}$内的$\rho$都是收敛的，因此$u$和$v$，即在半径为$\rho$的圆周上确定点的坐标，对于所有$\rho <\rho _{0}$的值都是唯一确定的。因此，至少在开始时，属于扇形的曲线实际上完全彼此分离。

第 93 条.
微分方程$G=0$的形式，其中$s$被引入作为自变量而不是$t$。 如果我们引入另一个变量$\tau$，代替$t$，并令$t$等于$\tau$的函数，我们得到相同的微分方程$G=0$。通常情况下，将弧长$s$作为自变量是有利的。

由于（第 68 条）函数$F$关于其第三个和第四个参数的导数是保持不变的，我们有（在第 68 条的公式中写$k={\frac {1}{\sqrt {x'^{2}+y'^{2}}}}={\frac {{\text{d}}t}{{\text{d}}s}}$)

${\frac {\partial }{\partial x'}}F(x,y,x',y,)={\frac {\partial }{\partial \left({\frac {{\text{d}}x}{{\text{d}}s}}\right)}}F\left(x,y,{\frac {{\text{d}}x}{{\text{d}}s}},{\frac {{\text{d}}y}{{\text{d}}s}}\right)$,

${\frac {\partial }{\partial y'}}F(x,y,x',y,)={\frac {\partial }{\partial \left({\frac {{\text{d}}y}{{\text{d}}s}}\right)}}F\left(x,y,{\frac {{\text{d}}x}{{\text{d}}s}},{\frac {{\text{d}}y}{{\text{d}}s}}\right)$.

由此可见，${\frac {\partial F}{\partial x'}}$，${\frac {\partial F}{\partial y'}}$ 与表达 $y$ 和 $y$ 为 $t$ 的函数的方式无关，而只取决于曲线上该点的坐标以及该点切线的方向。我们立即得到

${\frac {\partial ^{2}F}{\partial x'\partial y'}}={\frac {\partial ^{2}}{\partial {\frac {{\text{d}}x}{{\text{d}}s}}\partial {\frac {{\text{d}}y}{{\text{d}}s}}}}F\left(x,y,{\frac {{\text{d}}x}{{\text{d}}s}},{\frac {{\text{d}}y}{{\text{d}}s}}\right){\frac {1}{\frac {{\text{d}}s}{{\text{d}}t}}}$;

由于

$F_{1}=-{\frac {1}{x'y'}}{\frac {\partial ^{2}F(x,y,x',y')}{\partial x'\partial y'}}$,

因此，我们得到

$F_{1}\left({\frac {{\text{d}}s}{{\text{d}}t}}\right)^{3}=-{\frac {1}{{\frac {{\text{d}}x}{{\text{d}}s}}{\frac {{\text{d}}y}{{\text{d}}s}}}}{\frac {\partial ^{2}}{\partial {\frac {{\text{d}}x}{{\text{d}}s}}\partial {\frac {{\text{d}}y}{{\text{d}}s}}}}F\left(x,y,{\frac {{\text{d}}x}{{\text{d}}s}},{\frac {{\text{d}}y}{{\text{d}}s}}\right)$.

如果我们进一步写成

${\frac {\partial ^{2}}{\partial {\frac {{\text{d}}x}{{\text{d}}s}}\partial {\frac {{\text{d}}y}{{\text{d}}s}}}}F\left(x,y,{\frac {{\text{d}}x}{{\text{d}}s}},{\frac {{\text{d}}y}{{\text{d}}s}}\right)=-{\frac {{\text{d}}x}{{\text{d}}s}}{\frac {{\text{d}}y}{{\text{d}}s}}F_{1}\left(x,y,{\frac {{\text{d}}x}{{\text{d}}s}},{\frac {{\text{d}}y}{{\text{d}}s}}\right)$,

我们有

$F\left(x,y,{\frac {{\text{d}}x}{{\text{d}}s}},{\frac {{\text{d}}y}{{\text{d}}s}}\right)\left({\frac {{\text{d}}s}{{\text{d}}t}}\right)^{3}=F_{1}\left(x,y,{\frac {{\text{d}}x}{{\text{d}}s}},{\frac {{\text{d}}y}{{\text{d}}s}}\right)$.

因此方程$G=0$ 变为

${\frac {\partial ^{2}}{\partial x\partial {\frac {{\text{d}}y}{{\text{d}}s}}}}F\left(x,y,{\frac {{\text{d}}x}{{\text{d}}s}},{\frac {{\text{d}}y}{{\text{d}}s}}\right)-{\frac {\partial ^{2}}{\partial y\partial {\frac {{\text{d}}x}{{\text{d}}s}}}}F\left(x,y,{\frac {{\text{d}}x}{{\text{d}}s}},{\frac {{\text{d}}y}{{\text{d}}s}}\right)+\left({\frac {{\text{d}}x}{{\text{d}}s}}{\frac {{\text{d}}^{2}y}{{\text{d}}s^{2}}}-{\frac {{\text{d}}y}{{\text{d}}s}}{\frac {{\text{d}}^{2}x}{{\text{d}}s^{2}}}\right)F_{1}\left(x,y,{\frac {{\text{d}}x}{{\text{d}}s}},{\frac {{\text{d}}y}{{\text{d}}s}}\right)=0$.

第 94 条.
从上面的等式，$x$ 和 $y$ 关于 $s$ 的二阶及更高阶导数可以明确地用 $x$,$x$,${\frac {{\text{d}}x}{{\text{d}}s}}$,${\frac {{\text{d}}y}{{\text{d}}s}}$ 表示。

因为，从关系

$\left({\frac {{\text{d}}x}{{\text{d}}s}}\right)^{2}+\left({\frac {{\text{d}}y}{{\text{d}}s}}\right)^{2}=1$,

可以推导出，通过微分，得到

${\frac {{\text{d}}x}{{\text{d}}s}}{\frac {{\text{d}}^{2}x}{{\text{d}}s^{2}}}+{\frac {{\text{d}}y}{{\text{d}}s}}{\frac {{\text{d}}^{2}y}{{\text{d}}s^{2}}}=0$. $\qquad {\text{[i]}}$

为了简便，我们写成

${\frac {\partial ^{2}}{\partial x\partial {\frac {{\text{d}}y}{{\text{d}}s}}}}F\left(x,y,{\frac {{\text{d}}x}{{\text{d}}s}},{\frac {{\text{d}}y}{{\text{d}}s}}\right)-{\frac {\partial ^{2}}{\partial y\partial {\frac {{\text{d}}x}{{\text{d}}s}}}}F\left(x,y,{\frac {{\text{d}}x}{{\text{d}}s}},{\frac {{\text{d}}y}{{\text{d}}s}}\right)=H\left(x,y,{\frac {{\text{d}}x}{{\text{d}}s}},{\frac {{\text{d}}y}{{\text{d}}s}}\right)$,

我们可以将上一篇文章中的微分方程写成以下形式：

$F_{1}\left(x,y,{\frac {{\text{d}}x}{{\text{d}}s}},{\frac {{\text{d}}y}{{\text{d}}s}}\right)\left({\frac {{\text{d}}x}{{\text{d}}s}}{\frac {{\text{d}}^{2}y}{{\text{d}}s^{2}}}-{\frac {{\text{d}}y}{{\text{d}}s}}{\frac {{\text{d}}^{2}x}{{\text{d}}s^{2}}}\right)=H\left(x,y,{\frac {{\text{d}}x}{{\text{d}}s}},{\frac {{\text{d}}y}{{\text{d}}s}}\right)$

借助[i]，我们有

${\frac {{\text{d}}^{2}x}{{\text{d}}s^{2}}}F_{1}\left(x,y,{\frac {{\text{d}}x}{{\text{d}}s}},{\frac {{\text{d}}y}{{\text{d}}s}}\right)={\frac {{\text{d}}y}{{\text{d}}s}}H\left(x,y,{\frac {{\text{d}}x}{{\text{d}}s}},{\frac {{\text{d}}y}{{\text{d}}s}}\right)$, ${\frac {{\text{d}}^{2}y}{{\text{d}}s^{2}}}F_{1}\left(x,y,{\frac {{\text{d}}x}{{\text{d}}s}},{\frac {{\text{d}}y}{{\text{d}}s}}\right)=-{\frac {{\text{d}}y}{{\text{d}}s}}H\left(x,y,{\frac {{\text{d}}x}{{\text{d}}s}},{\frac {{\text{d}}y}{{\text{d}}s}}\right)$. $\qquad {\text{[ii]}}$

无需进一步解释即可说明如何从这些关系中表达 $x$ 和 $y$ 关于 $s$ 的三阶及更高阶导数，用 $x$， $y$， ${\frac {{\text{d}}x}{{\text{d}}s}}$ 和 ${\frac {{\text{d}}y}{{\text{d}}s}}$ 表示。

第 95 条.
因此，如果 $F_{1}$ 处处不为零，并且与 $H$ 一样，是其自变量的连续函数，并且如果 $H$ 从不趋于无穷大（参见第 149 条），那么，${\frac {{\text{d}}^{2}x}{{\text{d}}s^{2}}}$ 和 ${\frac {{\text{d}}^{2}y}{{\text{d}}s^{2}}}$ 从不趋于无穷大，并且也是弧长的连续函数。

由此可见，曲线在所讨论的区间内没有奇点，曲率也从不趋于无穷大。这可以通过以下方式证明：假设曲线上一点 $x_{0}$，$y_{0}$ 对应于 $s$ 的值 $s_{0}$，那么根据上一条中方程 [ii]，该点附近曲线的方程可以表示为

$x=x_{0}+A(s-s_{0})^{\mu }+\cdots$,

$y=y_{0}+B(s-s_{0})^{\mu }+\cdots$,

其中常數 $A$ 和 $B$ 不会同时消失。当从这些方程中推导出的 ${\frac {{\text{d}}x}{{\text{d}}s}}$ 和 ${\frac {{\text{d}}y}{{\text{d}}s}}$ 的值被代入

$\left({\frac {{\text{d}}x}{{\text{d}}s}}\right)^{2}+\left({\frac {{\text{d}}y}{{\text{d}}s}}\right)^{2}=1$,

因此，我们得到

$1=\mu ^{2}(A^{2}+B^{2})(s-s_{0})^{2\mu -2}+A_{1}(s-s_{0})^{2\mu -3}+\cdots$,

由于该方程对于 $x_{0}$，$y_{0}$ 邻域中的所有点都成立，可以看出

$A_{1}=A_{2}=\cdots =0$,

并且进一步可以看出

$\mu =1$，$A^{2}+B^{2}=1$。

因此，曲线位于 $x_{0}$，$y_{0}$ 邻域中的每个点的坐标都可以用正则函数表示

$x=x_{0}+A(s-s_{0})+\cdots$,

$y=y_{0}+B(s-s_{0})+\cdots$,

其中 $A$ 和 $B$ 不会同时消失。由于这对每个点 $x_{0}$，$y_{0}$ 都成立，因此曲线没有奇点。因此，$x'$ 和 $y'$ 不会同时消失。