Cg 编程/Unity/贝塞尔曲线

本教程讨论了在 Unity 中渲染二次贝塞尔曲线和样条的一种方法。这是几个教程中的第一个，演示了 Unity 有用的功能，这些功能与着色器没有直接关联；因此，不需要着色器编程，所有展示的代码都在 C# 中。

平滑曲线在计算机图形学中有很多应用，特别是在动画和建模中。在 3D 游戏引擎中，通常会使用管状网格，并通过顶点混合对其进行变形，如 “非线性变形”部分中所述，而不是渲染曲线；然而，渲染曲线而不是变形网格可以提供显著的性能优势。

线性贝塞尔曲线

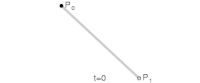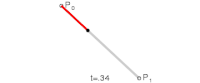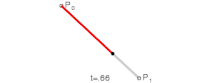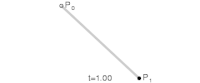
最简单的贝塞尔曲线是线性贝塞尔曲线 $B(t)$ ，对于 $t$ 从 0 到 1，在两点 $P_{0}$ 和 $P_{1}$ 之间，它恰好与这两点之间的线性插值相同

$B(t)=(1-t)P_{0}+tP_{1}$

你可能很时髦，称 $1-t$ 和 $t$ 为 1 次伯恩斯坦基多项式，但实际上它只是线性插值。

二次贝塞尔曲线

更有趣的贝塞尔曲线是二次贝塞尔曲线 $B(t)$ ，对于 $t$ 从 0 到 1，在两点 $P_{0}$ 和 $P_{2}$ 之间，但受中间的第三点 $P_{1}$ 的影响。定义是

$B(t)=(1-t)^{2}P_{0}+2(1-t)tP_{1}+t^{2}P_{2}$

这定义了一条平滑曲线 $B(t)$ ，其中 $t\in [0,1]$ ，从位置 $P_{0}$ 开始（当 $t=0$ ）朝向 $P_{1}$ ，然后弯曲到 $P_{2}$ （并在 $t=1$ 时到达那里）。

在实践中，人们通常会对从 0 到 1 的区间进行足够多的点采样，例如 $B(0),B(0.05),B(0.1),B(0.15),B(0.2),...,B(1)$ ，然后在这些采样点之间绘制直线。

曲线脚本

要在 Unity 中实现这种曲线，我们可以使用 Unity 组件 LineRenderer。除了设置一些参数外，还应该使用函数 SetVertexCount 设置曲线上采样点的数量。然后，需要计算采样点并使用函数 SetPosition 设置它们。这可以通过以下方式实现：

float t;
Vector3 position;
for(int i = 0; i < numberOfPoints; i++)
{
	t = i / (numberOfPoints - 1.0f);
	position = (1.0f - t) * (1.0f - t) * p0 + 2.0f * (1.0f - t) * t * p1 + t * t * p2;
	lineRenderer.SetPosition(i, position);
}

在这里，我们使用从 0 到 numberOfPoints-1 的索引 i 来计数采样点。从该索引 i 计算出从 0 到 1 的参数 t。下一行计算 $B(t)$ ，然后使用函数 SetPosition 设置它。

代码的其余部分只是设置 LineRenderer 组件并定义可用于定义控制点和曲线的某些渲染功能的公共变量。

using UnityEngine;

[ExecuteInEditMode, RequireComponent(typeof(LineRenderer))]
public class Bezier_Curve : MonoBehaviour 
{
	public GameObject start, middle, end;
	public Color color = Color.white;
	public float width = 0.2f;
	public int numberOfPoints = 20;
	LineRenderer lineRenderer;

	void Start () 
	{
		lineRenderer = GetComponent<LineRenderer>();
		lineRenderer.useWorldSpace = true;
		lineRenderer.material = new Material(Shader.Find("Legacy Shaders/Particles/Additive"));
	}
	
	void Update () 
	{
		if( lineRenderer == null || start == null || middle == null || end == null)
		{
			return; // no points specified
		}

		// update line renderer
		lineRenderer.startColor = color;
		lineRenderer.endColor = color;
   		lineRenderer.startWidth = width;
		lineRenderer.endWidth = width;

  		if (numberOfPoints > 0)
   		{
    			lineRenderer.positionCount = numberOfPoints;
		}

		// set points of quadratic Bezier curve
		Vector3 p0 = start.transform.position;
		Vector3 p1 = middle.transform.position;
		Vector3 p2 = end.transform.position;
		float t;
		Vector3 position;
		for(int i = 0; i < numberOfPoints; i++)
		{
			t = i / (numberOfPoints - 1.0f);
			position = (1.0f - t) * (1.0f - t) * p0 
			+ 2.0f * (1.0f - t) * t * p1 + t * t * p2;
			lineRenderer.SetPosition(i, position);
		}
	}
}

要使用此脚本，请在 **项目窗口** 中 **创建** 一个 **C# 脚本** 并将其命名为 **Bezier_Curve**，双击它，复制并粘贴上面的代码，保存它，创建一个新的空游戏对象（在主菜单中：**游戏对象>创建空**），然后将脚本附加到它（将脚本从 **项目窗口** 拖动到 **层次结构窗口** 中的空游戏对象上）。

然后创建另外三个空游戏对象（或任何其他游戏对象），这些游戏对象将具有不同的位置，用作控制点。选择带有脚本的游戏对象，并将其他游戏对象拖动到 **检查器** 中的 **开始**、**中间** 和 **结束** 槽位中。这将从指定为“开始”的游戏对象渲染一条曲线，到指定为“结束”的游戏对象，并朝“中间”弯曲。

二次贝塞尔样条曲线

二次贝塞尔样条曲线只是一条连续的、平滑的曲线，它由二次贝塞尔曲线段组成。如果曲线的控制点是任意选择的，那么样条曲线将既不连续也不平滑；因此，必须以特定方式选择控制点。

一种常见的方法是使用一组用户指定的控制点（图中的绿色圆圈）作为各段的 $P_{1}$ 控制点，并选择相邻两个用户指定控制点之间的中心位置作为 $P_{0}$ 和 $P_{2}$ 控制点（图中的黑色矩形）。这实际上保证了样条曲线是平滑的（在数学意义上也是连续的切向量）。

样条曲线脚本

以下脚本实现了这个想法。对于第 j 个段，它计算 $P_{0}$ 作为第 j 个和第 (j+1) 个用户指定的控制点的平均值， $P_{1}$ 设置为第 (j+1) 个用户指定的控制点，以及 $P_{2}$ 是第 (j+1) 个和第 (j+2) 个用户指定的控制点的平均值。

      p0 = 0.5f * (controlPoints[j].transform.position 
         + controlPoints[j + 1].transform.position);
      p1 = controlPoints[j + 1].transform.position;
      p2 = 0.5f * (controlPoints[j + 1].transform.position 
         + controlPoints[j + 2].transform.position);

然后，每个单独的段都被计算为二次贝塞尔曲线。唯一的调整是，除了最后一个段之外，所有段都不应该达到 $P_{2}$ 。如果它们确实达到了，那么下一段的第一个样本位置将位于相同的位置，这将在渲染中可见。完整的脚本是

using System.Collections.Generic;
using UnityEngine;

[ExecuteInEditMode, RequireComponent(typeof(LineRenderer))]
public class Bezier_Spline : MonoBehaviour 
{
	public List<GameObject> controlPoints = new List<GameObject>();
	public Color color = Color.white;
	public float width = 0.2f;
	public int numberOfPoints = 20;
	LineRenderer lineRenderer;

	void Start () 
	{
		lineRenderer = GetComponent<LineRenderer>();
		lineRenderer.useWorldSpace = true;
		lineRenderer.material = new Material(Shader.Find("Legacy Shaders/Particles/Additive"));
	}
	
	
	void Update () 
	{
		if (null == lineRenderer || controlPoints == null || controlPoints.Count < 3)
    		{
       			return; // not enough points specified
   		}
		// update line renderer
		lineRenderer.startColor = color;
		lineRenderer.endColor = color;
   		lineRenderer.startWidth = width;
		lineRenderer.endWidth = width;

		if(numberOfPoints < 2)
		{
			numberOfPoints = 2;
		} 
		lineRenderer.positionCount = numberOfPoints * (controlPoints.Count - 2);

		Vector3 p0, p1 ,p2;
		for(int j = 0; j < controlPoints.Count - 2; j++)
		{
			// check control points
			if (controlPoints[j] == null || controlPoints[j + 1] == null 
			|| controlPoints[j + 2] == null)
			{
				return;  
			}
			// determine control points of segment
			p0 = 0.5f * (controlPoints[j].transform.position 
			+ controlPoints[j + 1].transform.position);
			p1 = controlPoints[j + 1].transform.position;
			p2 = 0.5f * (controlPoints[j + 1].transform.position 
			+ controlPoints[j + 2].transform.position);
			
			// set points of quadratic Bezier curve
			Vector3 position;
			float t;
			float pointStep = 1.0f / numberOfPoints;
			if (j == controlPoints.Count - 3)
			{
				pointStep = 1.0f / (numberOfPoints - 1.0f);
				// last point of last segment should reach p2
			}  
			for(int i = 0; i < numberOfPoints; i++) 
			{
				t = i * pointStep;
				position = (1.0f - t) * (1.0f - t) * p0 
				+ 2.0f * (1.0f - t) * t * p1 + t * t * p2;
				lineRenderer.SetPosition(i + j * numberOfPoints, position);
			}
		}
	}
}

该脚本必须命名为 Bezier_Spline，并且与贝塞尔曲线的脚本工作方式相同，只是用户可以指定任意数量的控制点。对于闭合样条曲线，最后两个用户指定的控制点应与前两个控制点相同。对于实际上到达端点的开放样条曲线，应两次指定第一个和最后一个控制点。

总结

在本教程中，我们已经了解了

线性贝塞尔曲线和二次贝塞尔曲线以及二次贝塞尔样条曲线的定义
使用 Unity 的 LineRenderer 组件实现二次贝塞尔曲线和二次贝塞尔样条曲线。

进一步阅读

如果您想了解更多

关于贝塞尔曲线（和贝塞尔样条曲线），维基百科关于 “贝塞尔曲线” 的文章提供了一个良好的起点。
关于 Unity 的 LineRenderer，您应该阅读 Unity 关于类 LineRenderer 的文档。

< Cg 编程/Unity

除非另有说明，否则此页面上的所有示例源代码均授予公共领域。