顶点着色器和可编程图形管道中后续阶段最重要的任务之一是将图元(例如三角形)的顶点从原始坐标(例如在 3D 建模工具中指定的坐标)变换到屏幕坐标。虽然可编程顶点着色器允许以多种方式变换顶点,但一些变换通常在顶点着色器之后的固定功能阶段执行。因此,在编程顶点着色器时,了解哪些变换必须在顶点着色器中执行尤为重要。这些变换通常作为统一参数指定,并通过矩阵向量乘法应用于输入顶点位置(和法线向量)。在具有输入参数 vertex : POSITION 的顶点着色器中,标准变换可以通过此矩阵向量积计算
mul ( UNITY_MATRIX_MVP , vertex )
Unity 的内置统一参数 UNITY_MATRIX_MVP 将标准顶点变换指定为 4x4 矩阵。(但是,在 Unity 中,建议使用函数 UnityObjectToClipPos(vertex) 执行此变换,该函数也适用于立体投影和投影到 360 图像等。)
虽然这对于点和方向来说很简单,但正如“应用矩阵变换”一节 中所述,对于法线向量来说就不那么简单了。
这里,我们将首先概述坐标系以及它们之间的变换,然后讨论各个变换。
相机类比:1. 定位模型,2. 定位相机,3. 调整缩放,4. 裁剪图像 用相机类比来思考变换顶点的整个过程非常有用,如右图所示。步骤和相应的顶点变换是
定位模型 - 模型变换
定位相机 - 观察变换
调整缩放 - 投影变换
裁剪图像 - 视口变换 前三个变换在顶点着色器中应用。然后,透视除法(可以认为是投影变换的一部分)在顶点着色器之后的固定功能阶段自动应用。视口变换也在此固定功能阶段自动应用。虽然固定功能阶段中的变换无法修改,但其他变换可以被这里描述的其他类型的变换所取代。但是,了解传统的变换很有用,因为它们允许充分利用裁剪和对变化变量的透视正确插值。
以下概述显示了各种坐标系之间顶点变换的顺序,并包括表示变换的矩阵
对象/模型坐标
具有语义的顶点输入参数(特别是语义 POSITION)
↓
模型变换 : 模型矩阵 M object → world {\displaystyle \mathrm {M} _{{\text{object}}\to {\text{world}}}} unity_ObjectToWorld)
世界坐标
↓
观察变换 : 观察矩阵 M world → view {\displaystyle \mathrm {M} _{{\text{world}}\to {\text{view}}}} UNITY_MATRIX_V)
观察/眼睛坐标
↓
投影变换 : 投影矩阵 M projection {\displaystyle \mathrm {M} _{\text{projection}}} UNITY_MATRIX_P)
裁剪坐标
具有语义 SV_POSITION 的顶点输出参数
↓
透视除法 (除以 w 坐标)
归一化设备坐标
↓
视口变换
屏幕/窗口坐标
请注意,模型、观察和投影变换在顶点着色器中应用。透视除法和视口变换在顶点着色器之后的固定功能阶段应用。接下来的部分将详细讨论所有这些变换。
模型变换指定从对象坐标(也称为模型坐标或局部坐标)到公共世界坐标系的变换。对象坐标通常特定于每个对象或模型,并且通常在 3D 建模工具中指定。另一方面,世界坐标是场景中所有对象的公共坐标系,包括光源、3D 音频源等。由于不同的对象具有不同的对象坐标系,因此模型变换也不同;即,必须对每个对象应用不同的模型变换。
模型变换可以用 4×4 矩阵表示,我们将其表示为模型矩阵 M object → world {\displaystyle \mathrm {M} _{{\text{object}}\to {\text{world}}}} unity_ObjectToWorld)。它的结构是
M object → world = [ a 1 , 1 a 1 , 2 a 1 , 3 t 1 a 2 , 1 a 2 , 2 a 2 , 3 t 2 a 3 , 1 a 3 , 2 a 3 , 3 t 3 0 0 0 1 ] {\displaystyle \mathrm {M} _{{\text{object}}\to {\text{world}}}=\left[{\begin{matrix}a_{1,1}&a_{1,2}&a_{1,3}&t_{1}\\a_{2,1}&a_{2,2}&a_{2,3}&t_{2}\\a_{3,1}&a_{3,2}&a_{3,3}&t_{3}\\0&0&0&1\end{matrix}}\right]} with A = [ a 1 , 1 a 1 , 2 a 1 , 3 a 2 , 1 a 2 , 2 a 2 , 3 a 3 , 1 a 3 , 2 a 3 , 3 ] {\displaystyle {\text{ with }}\mathrm {A} =\left[{\begin{matrix}a_{1,1}&a_{1,2}&a_{1,3}\\a_{2,1}&a_{2,2}&a_{2,3}\\a_{3,1}&a_{3,2}&a_{3,3}\end{matrix}}\right]} and t = [ t 1 t 2 t 3 ] {\displaystyle {\text{ and }}\mathbf {t} =\left[{\begin{matrix}t_{1}\\t_{2}\\t_{3}\end{matrix}}\right]}
A {\displaystyle \mathrm {A} } t 是一个 3D 向量,表示 3D 空间中的平移(即位移)。 M object → world {\displaystyle \mathrm {M} _{{\text{object}}\to {\text{world}}}} A {\displaystyle \mathrm {A} } t 结合在一个方便的 4×4 矩阵中。从数学上来说,模型矩阵表示仿射变换:线性变换加上平移。为了使这种方法起作用,所有三维点都由具有第四坐标为 1 的四维向量表示
P = [ p 1 p 2 p 3 1 ] {\displaystyle P=\left[{\begin{matrix}p_{1}\\p_{2}\\p_{3}\\1\end{matrix}}\right]}
当我们将矩阵乘以这样的点 P {\displaystyle P}
M object → world P = [ a 1 , 1 a 1 , 2 a 1 , 3 t 1 a 2 , 1 a 2 , 2 a 2 , 3 t 2 a 3 , 1 a 3 , 2 a 3 , 3 t 3 0 0 0 1 ] [ p 1 p 2 p 3 1 ] {\displaystyle \mathrm {M} _{{\text{object}}\to {\text{world}}}\;P=\left[{\begin{matrix}a_{1,1}&a_{1,2}&a_{1,3}&t_{1}\\a_{2,1}&a_{2,2}&a_{2,3}&t_{2}\\a_{3,1}&a_{3,2}&a_{3,3}&t_{3}\\0&0&0&1\end{matrix}}\right]\left[{\begin{matrix}p_{1}\\p_{2}\\p_{3}\\1\end{matrix}}\right]} = [ a 1 , 1 p 1 + a 1 , 2 p 2 + a 1 , 3 p 3 + t 1 a 2 , 1 p 1 + a 2 , 2 p 2 + a 2 , 3 p 3 + t 2 a 3 , 1 p 1 + a 3 , 2 p 2 + a 3 , 3 p 3 + t 3 1 ] {\displaystyle =\left[{\begin{matrix}a_{1,1}p_{1}+a_{1,2}p_{2}+a_{1,3}p_{3}+t_{1}\\a_{2,1}p_{1}+a_{2,2}p_{2}+a_{2,3}p_{3}+t_{2}\\a_{3,1}p_{1}+a_{3,2}p_{2}+a_{3,3}p_{3}+t_{3}\\1\end{matrix}}\right]}
除了第四个坐标(它应该是点位的 1),结果等于
A [ p 1 p 2 p 3 ] + [ t 1 t 2 t 3 ] {\displaystyle \mathrm {A} \left[{\begin{matrix}p_{1}\\p_{2}\\p_{3}\end{matrix}}\right]+\left[{\begin{matrix}t_{1}\\t_{2}\\t_{3}\end{matrix}}\right]}
模型矩阵 M object → world {\displaystyle \mathrm {M} _{{\text{object}}\to {\text{world}}}} unity_ObjectToWorld。(另请参见 “应用矩阵变换”部分 。)
严格来说,Cg 程序员不必担心模型矩阵的计算,因为它以统一参数的形式提供给顶点着色器。实际上,渲染引擎、场景图和游戏引擎通常会提供模型矩阵;因此,顶点着色器的程序员不必担心计算模型矩阵。然而,在某些情况下,在开发图形应用程序时必须计算模型矩阵。
模型矩阵通常通过组合对象的初等变换的 4×4 矩阵来计算,特别是平移、旋转和缩放。具体来说,在层次场景图的情况下,将对象的全部父组(父级、祖父母等)的变换组合起来形成模型矩阵。让我们看一下最重要的初等变换及其矩阵。
表示向量 t = ( t 1 , t 2 , t 3 ) {\displaystyle =(t_{1},t_{2},t_{3})}
M translation = [ 1 0 0 t 1 0 1 0 t 2 0 0 1 t 3 0 0 0 1 ] {\displaystyle \mathrm {M} _{\text{translation}}=\left[{\begin{matrix}1&0&0&t_{1}\\0&1&0&t_{2}\\0&0&1&t_{3}\\0&0&0&1\end{matrix}}\right]}
表示沿 x {\displaystyle x} s x {\displaystyle s_{x}} y {\displaystyle y} s y {\displaystyle s_{y}} z {\displaystyle z} s z {\displaystyle s_{z}}
M scaling = [ s x 0 0 0 0 s y 0 0 0 0 s z 0 0 0 0 1 ] {\displaystyle \mathrm {M} _{\text{scaling}}=\left[{\begin{matrix}s_{x}&0&0&0\\0&s_{y}&0&0\\0&0&s_{z}&0\\0&0&0&1\end{matrix}}\right]}
表示绕归一化轴 ( x , y , z ) {\displaystyle (x,y,z)} α {\displaystyle \alpha }
M rotation = [ ( 1 − cos α ) x x + cos α ( 1 − cos α ) x y − z sin α ( 1 − cos α ) z x + y sin α 0 ( 1 − cos α ) x y + z sin α ( 1 − cos α ) y y + cos α ( 1 − cos α ) y z − x sin α 0 ( 1 − cos α ) z x − y sin α ( 1 − cos α ) y z + x sin α ( 1 − cos α ) z z + cos α 0 0 0 0 1 ] {\displaystyle \mathrm {M} _{\text{rotation}}=\left[{\begin{matrix}(1-\cos \alpha )x\,x+\cos \alpha &(1-\cos \alpha )x\,y-z\sin \alpha &(1-\cos \alpha )z\,x+y\sin \alpha &0\\(1-\cos \alpha )x\,y+z\sin \alpha &(1-\cos \alpha )y\,y+\cos \alpha &(1-\cos \alpha )y\,z-x\sin \alpha &0\\(1-\cos \alpha )z\,x-y\sin \alpha &(1-\cos \alpha )y\,z+x\sin \alpha &(1-\cos \alpha )z\,z+\cos \alpha &0\\0&0&0&1\end{matrix}}\right]}
绕特定轴的旋转可以很容易地推导出特殊情况。例如,这些情况对于实现欧拉角旋转是必要的。但是,欧拉角有多种约定,这里不会讨论。
一个标准化的四元数 ( x q , y q , z q , w q ) {\displaystyle (x_{q},y_{q},z_{q},w_{q})} 2 arccos ( w q ) {\displaystyle 2\arccos(w_{q})} ( x q , y q , z q ) {\displaystyle (x_{q},y_{q},z_{q})}
还有其他基本的变换,但对模型矩阵的计算而言并不那么重要。这些或其他变换的 4x4 矩阵通过矩阵乘积进行组合。假设矩阵 M 1 {\displaystyle \mathrm {M} _{1}} M 2 {\displaystyle \mathrm {M} _{2}} M 3 {\displaystyle \mathrm {M} _{3}} M 1 {\displaystyle \mathrm {M} _{1}} M 2 {\displaystyle \mathrm {M} _{2}} M 3 {\displaystyle \mathrm {M} _{3}}
M combined = M 3 M 2 M 1 {\displaystyle \mathrm {M} _{\text{combined}}=\mathrm {M} _{3}\mathrm {M} _{2}\mathrm {M} _{1}\,\!}
请注意,矩阵因子的顺序很重要。还要注意,这个矩阵乘积应该从右(向量被乘的地方)读到左,即 M 1 {\displaystyle \mathrm {M} _{1}} M 3 {\displaystyle \mathrm {M} _{3}}
视图坐标系的示意图。 观察变换对应于放置和定向相机(或观察者的眼睛)。 但是,看待观察变换的最佳方式是,它将世界坐标转换为位于坐标系原点的相机的视图坐标系(也称为眼睛坐标系),(按惯例)指向负 z {\displaystyle z} 正 z {\displaystyle z} x z {\displaystyle xz} y {\displaystyle y}
与模型变换类似,观察变换由一个4×4矩阵表示,称为视图矩阵 M world → view {\displaystyle \mathrm {M} _{{\text{world}}\to {\text{view}}}} UNITY_MATRIX_V); 但是,它通常与模型矩阵 M object → world {\displaystyle \mathrm {M} _{{\text{object}}\to {\text{world}}}} M object → view {\displaystyle \mathrm {M} _{{\text{object}}\to {\text{view}}}} UNITY_MATRIX_MV)。 由于模型矩阵先应用,正确的组合是
M object → view = M world → view M object → world {\displaystyle \mathrm {M} _{{\text{object}}\to {\text{view}}}=\mathrm {M} _{{\text{world}}\to {\text{view}}}\mathrm {M} _{{\text{object}}\to {\text{world}}}\,\!}
(另请参见部分“应用矩阵变换” 。)
与模型矩阵类似,Cg 程序员不必担心视图矩阵的计算,因为它是以统一参数的形式提供给顶点着色器的。 但是,在开发图形应用程序时,有时有必要计算视图矩阵。
这里,我们简要总结了如何从相机的t 位置、视图方向d 和世界向上向量k (全部以世界坐标表示)计算视图矩阵 M world → view {\displaystyle \mathrm {M} _{{\text{world}}\to {\text{view}}}} 负 z {\displaystyle z}
1. 计算(在世界坐标中)视图坐标系的 z {\displaystyle z} z ,作为负归一化的d 向量
z = − d | d | {\displaystyle \mathbf {z} =-{\frac {\mathbf {d} }{|\mathbf {d} |}}}
2. 计算(同样在世界坐标中)视图坐标系的 x {\displaystyle x} x ,通过
x = d × k | d × k | {\displaystyle \mathbf {x} ={\frac {\mathbf {d} \times \mathbf {k} }{|\mathbf {d} \times \mathbf {k} |}}}
3. 在世界坐标系中计算视图坐标系 y {\displaystyle y} y
y = z × x {\displaystyle \mathbf {y} =\mathbf {z} \times \mathbf {x} }
使用 x 、y 、z 和 t ,可以轻松确定逆视图矩阵 M view → world {\displaystyle \mathrm {M} _{{\text{view}}\to {\text{world}}}} t ,并将单位向量 (1,0,0)、(0,1,0) 和 (0,0,1) 映射到 x 、y, 、z 。因此,后面的向量必须位于矩阵 M view → world {\displaystyle \mathrm {M} _{{\text{view}}\to {\text{world}}}}
M view → world = [ x 1 y 1 z 1 t 1 x 2 y 2 z 2 t 2 x 3 y 3 z 3 t 3 0 0 0 1 ] {\displaystyle \mathrm {M} _{{\text{view}}\to {\text{world}}}=\left[{\begin{matrix}x_{1}&y_{1}&z_{1}&t_{1}\\x_{2}&y_{2}&z_{2}&t_{2}\\x_{3}&y_{3}&z_{3}&t_{3}\\0&0&0&1\end{matrix}}\right]}
然而,我们需要矩阵 M world → view {\displaystyle \mathrm {M} _{{\text{world}}\to {\text{view}}}} M view → world {\displaystyle \mathrm {M} _{{\text{view}}\to {\text{world}}}} M view→world {\displaystyle \mathrm {M} _{\text{view→world}}}
M view → world = [ R t 0 T 1 ] {\displaystyle \mathrm {M} _{{\text{view}}\to {\text{world}}}=\left[{\begin{matrix}\mathrm {R} &\mathbf {t} \\\mathbf {0} ^{T}&1\end{matrix}}\right]}
其中 R {\displaystyle \mathrm {R} } t 是一个 3D 向量。这种矩阵的逆矩阵是
M view → world − 1 = M world → view = [ R − 1 − R − 1 t 0 T 1 ] {\displaystyle \mathrm {M} _{{\text{view}}\to {\text{world}}}^{-1}=\mathrm {M} _{{\text{world}}\to {\text{view}}}=\left[{\begin{matrix}\mathrm {R} ^{-1}&-\mathrm {R} ^{-1}\mathbf {t} \\\mathbf {0} ^{T}&1\end{matrix}}\right]}
在本例中,矩阵 R {\displaystyle \mathrm {R} } R {\displaystyle \mathrm {R} }
M world → view = [ R T − R T t 0 T 1 ] {\displaystyle \mathrm {M} _{{\text{world}}\to {\text{view}}}=\left[{\begin{matrix}\mathrm {R} ^{T}&-\mathrm {R} ^{T}\mathbf {t} \\\mathbf {0} ^{T}&1\end{matrix}}\right]} with R = [ x 1 y 1 z 1 x 2 y 2 z 2 x 3 y 3 z 3 ] {\displaystyle {\text{with }}\mathrm {R} =\left[{\begin{matrix}x_{1}&y_{1}&z_{1}\\x_{2}&y_{2}&z_{2}\\x_{3}&y_{3}&z_{3}\end{matrix}}\right]}
虽然推导出这个结果需要一些线性代数知识,但最终的计算只需要基本的向量和矩阵运算,并且可以轻松地在任何常见的编程语言中实现。
文艺复兴时期的透视绘画:“男人画鲁特琴”由阿尔布雷希特·丢勒创作,1525 年 首先,投影变换决定投影的类型,例如透视或正交。透视投影对应于具有缩短效果的线性透视,而正交投影是不具有缩短效果的正交投影。缩短效果实际上是通过透视除法实现的;但是,控制透视投影的所有参数都在投影变换中设置。
从技术角度来说,投影变换将视图坐标转换为裁剪坐标。(场景可见部分之外的所有图元部分都在裁剪坐标中被裁剪掉。)它应该是顶点着色器中应用于顶点的最后一个变换,在顶点以语义 SV_POSITION 输出参数返回之前。然后,这些裁剪坐标通过 **透视除法** 转换为归一化设备坐标,这只是将所有坐标除以第四个坐标。(归一化设备坐标之所以被称为这个名字,是因为它们的值在场景可见部分的所有点的 -1 到 +1 之间。)
与模型变换和视图变换类似,投影变换也由一个 4×4 矩阵表示,称为投影矩阵 M projection {\displaystyle \mathrm {M} _{\text{projection}}} UNITY_MATRIX_P)。
与模型视图矩阵类似,Cg 程序员不必担心投影矩阵的计算。但是,在开发应用程序时,有时需要计算投影矩阵。
这里,我们展示了三种情况下的投影矩阵(所有情况都是针对 OpenGL 约定,即相机指向视图坐标中的负 z {\displaystyle z}
标准透视投影(对应于 OpenGL 2.x 函数 gluPerspective)
斜透视投影(对应于 OpenGL 2.x 函数 glFrustum)
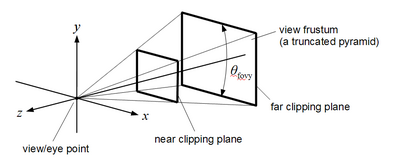
正交投影(对应于 OpenGL 2.x 函数 glOrtho) 角度 θ fovy {\displaystyle \theta _{\text{fovy}}} 以下是近裁剪平面和远裁剪平面在 z = − n {\displaystyle z=-n} z = − f {\displaystyle z=-f} 标准透视投影 的特点是
一个角度 θ fovy {\displaystyle \theta _{\text{fovy}}} y {\displaystyle y}
到近裁剪平面的距离 n {\displaystyle n} f {\displaystyle f}
近裁剪平面上中心矩形的宽高比 a {\displaystyle a} 与视点和裁剪平面一起,这个中心矩形定义了视锥体,即对于特定投影变换可见的 3D 空间区域。视锥体外的所有基本图形和所有基本图形的部分都被裁剪掉。近裁剪平面和远裁剪平面是必要的,因为深度值以有限精度存储;因此,不可能覆盖无限大的视锥体。
使用参数 θ fovy {\displaystyle \theta _{\text{fovy}}} a {\displaystyle a} n {\displaystyle n} f {\displaystyle f} M projection {\displaystyle \mathrm {M} _{\text{projection}}}
M projection = [ d a 0 0 0 0 d 0 0 0 0 n + f n − f 2 n f n − f 0 0 − 1 0 ] {\displaystyle \mathrm {M} _{\text{projection}}=\left[{\begin{matrix}{\frac {d}{a}}&0&0&0\\0&d&0&0\\0&0&{\frac {n+f}{n-f}}&{\frac {2nf}{n-f}}\\0&0&-1&0\end{matrix}}\right]} with d = 1 tan ( θ fovy / 2 ) {\displaystyle {\text{ with }}d={\frac {1}{\tan(\theta _{\text{fovy}}/2)}}}
斜透视投影的参数。 斜透视投影 的特点是
与标准透视投影情况相同,到裁剪平面的距离 n {\displaystyle n} f {\displaystyle f}
坐标 r {\displaystyle r} l {\displaystyle l} t {\displaystyle t} b {\displaystyle b} a {\displaystyle a} θ fovy {\displaystyle \theta _{\text{fovy}}} 给定参数 n {\displaystyle n} f {\displaystyle f} r {\displaystyle r} l {\displaystyle l} t {\displaystyle t} b {\displaystyle b} M projection {\displaystyle \mathrm {M} _{\text{projection}}}
M projection = [ 2 n r − l 0 r + l r − l 0 0 2 n t − b t + b t − b 0 0 0 n + f n − f 2 n f n − f 0 0 − 1 0 ] {\displaystyle \mathrm {M} _{\text{projection}}=\left[{\begin{matrix}{\frac {2n}{r-l}}&0&{\frac {r+l}{r-l}}&0\\0&{\frac {2n}{t-b}}&{\frac {t+b}{t-b}}&0\\0&0&{\frac {n+f}{n-f}}&{\frac {2nf}{n-f}}\\0&0&-1&0\end{matrix}}\right]}
正投影的参数。 右图说明了正投影 ,它没有透视缩短。参数与斜视投影的情况相同;但是,视锥体(更准确地说,是视体积)现在是一个盒子,而不是一个截断的金字塔。
使用参数 n {\displaystyle n} f {\displaystyle f} r {\displaystyle r} l {\displaystyle l} t {\displaystyle t} b {\displaystyle b} M projection {\displaystyle \mathrm {M} _{\text{projection}}}
M projection = [ 2 r − l 0 0 − r + l r − l 0 2 t − b 0 − t + b t − b 0 0 − 2 f − n − f + n f − n 0 0 0 1 ] {\displaystyle \mathrm {M} _{\text{projection}}=\left[{\begin{matrix}{\frac {2}{r-l}}&0&0&-{\frac {r+l}{r-l}}\\0&{\frac {2}{t-b}}&0&-{\frac {t+b}{t-b}}\\0&0&{\frac {-2}{f-n}}&-{\frac {f+n}{f-n}}\\0&0&0&1\end{matrix}}\right]}
视口变换的示意图。 投影变换将视图坐标映射到裁剪坐标,然后通过裁剪坐标的第四个分量进行透视除法,映射到归一化设备坐标。在归一化设备坐标(ndc)中,视图体积始终是一个以原点为中心的方框,方框内的坐标介于 -1 和 +1 之间。然后,该方框通过视口变换映射到屏幕坐标(也称为窗口坐标),如相应图形所示。此映射的参数是视口(屏幕上渲染的矩形)的左下角坐标 s x {\displaystyle s_{x}} s y {\displaystyle s_{y}} w s {\displaystyle w_{s}} h s {\displaystyle h_{s}} n s {\displaystyle n_{s}} f s {\displaystyle f_{s}}
glViewport(GLint s x {\displaystyle s_{x}} , GLint s y {\displaystyle s_{y}} , GLsizei w s {\displaystyle w_{s}} , GLsizei h s {\displaystyle h_{s}} );
glDepthRangef(GLclampf n s {\displaystyle n_{s}} , GLclampf f s {\displaystyle f_{s}} );
视口变换矩阵并不重要,因为它在固定功能阶段自动应用。但是,为了完整起见,这里列出它。
[ w s 2 0 0 s x + w s 2 0 h s 2 0 s y + h s 2 0 0 f s − n s 2 n s + f s 2 0 0 0 1 ] {\displaystyle \left[{\begin{matrix}{\frac {w_{s}}{2}}&0&0&s_{x}+{\frac {w_{s}}{2}}\\0&{\frac {h_{s}}{2}}&0&s_{y}+{\frac {h_{s}}{2}}\\0&0&{\frac {f_{s}-n_{s}}{2}}&{\frac {n_{s}+f_{s}}{2}}\\0&0&0&1\end{matrix}}\right]}
传统的顶点变换在Nvidia 的 Cg 教程第 4 章 中也进行了简要说明。
传统的 OpenGL 变换在“OpenGL 4.1 Compatibility Profile Specification”第 2.12 节中进行了详细描述,该规范可以在Khronos OpenGL 网站 上获得。Dave Shreiner 编著的“OpenGL Programming Guide”一书的第 3 章(关于查看)对顶点变换进行了更易懂的描述。该书由 Addison-Wesley 出版。(旧版可在网上 获得)。
< Cg 编程
除非另有说明,本页上的所有示例源代码均归属公共领域。











![{\displaystyle \mathrm {M} _{{\text{object}}\to {\text{world}}}=\left[{\begin{matrix}a_{1,1}&a_{1,2}&a_{1,3}&t_{1}\\a_{2,1}&a_{2,2}&a_{2,3}&t_{2}\\a_{3,1}&a_{3,2}&a_{3,3}&t_{3}\\0&0&0&1\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/74f8aaab560e5cb2f74f328599b57b54638f29f6)
![{\displaystyle {\text{ with }}\mathrm {A} =\left[{\begin{matrix}a_{1,1}&a_{1,2}&a_{1,3}\\a_{2,1}&a_{2,2}&a_{2,3}\\a_{3,1}&a_{3,2}&a_{3,3}\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dcff6fb39a87563940e5b11f2cd33c100e98d8de)
![{\displaystyle {\text{ and }}\mathbf {t} =\left[{\begin{matrix}t_{1}\\t_{2}\\t_{3}\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1762d98b5711974550f359f7b06264db7c931360)

![{\displaystyle P=\left[{\begin{matrix}p_{1}\\p_{2}\\p_{3}\\1\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa4c63dd467c6eb272d3b11d2dcb27c641be56bf)

![{\displaystyle \mathrm {M} _{{\text{object}}\to {\text{world}}}\;P=\left[{\begin{matrix}a_{1,1}&a_{1,2}&a_{1,3}&t_{1}\\a_{2,1}&a_{2,2}&a_{2,3}&t_{2}\\a_{3,1}&a_{3,2}&a_{3,3}&t_{3}\\0&0&0&1\end{matrix}}\right]\left[{\begin{matrix}p_{1}\\p_{2}\\p_{3}\\1\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13d11dfa872a62f11d49f0b7594bea2e57f36ab1)
![{\displaystyle =\left[{\begin{matrix}a_{1,1}p_{1}+a_{1,2}p_{2}+a_{1,3}p_{3}+t_{1}\\a_{2,1}p_{1}+a_{2,2}p_{2}+a_{2,3}p_{3}+t_{2}\\a_{3,1}p_{1}+a_{3,2}p_{2}+a_{3,3}p_{3}+t_{3}\\1\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f96ff85224b8f3fb35ccd73c31b54bd69cca25d)
![{\displaystyle \mathrm {A} \left[{\begin{matrix}p_{1}\\p_{2}\\p_{3}\end{matrix}}\right]+\left[{\begin{matrix}t_{1}\\t_{2}\\t_{3}\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ff6335e75528b3f090325320d6db5f829863e54e)

![{\displaystyle \mathrm {M} _{\text{translation}}=\left[{\begin{matrix}1&0&0&t_{1}\\0&1&0&t_{2}\\0&0&1&t_{3}\\0&0&0&1\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a9ccb86cb24fb7ce0bf772f83efbb7391c312146)






![{\displaystyle \mathrm {M} _{\text{scaling}}=\left[{\begin{matrix}s_{x}&0&0&0\\0&s_{y}&0&0\\0&0&s_{z}&0\\0&0&0&1\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b366a6c227cafdd36ec11f98948bc514b42ef014)


![{\displaystyle \mathrm {M} _{\text{rotation}}=\left[{\begin{matrix}(1-\cos \alpha )x\,x+\cos \alpha &(1-\cos \alpha )x\,y-z\sin \alpha &(1-\cos \alpha )z\,x+y\sin \alpha &0\\(1-\cos \alpha )x\,y+z\sin \alpha &(1-\cos \alpha )y\,y+\cos \alpha &(1-\cos \alpha )y\,z-x\sin \alpha &0\\(1-\cos \alpha )z\,x-y\sin \alpha &(1-\cos \alpha )y\,z+x\sin \alpha &(1-\cos \alpha )z\,z+\cos \alpha &0\\0&0&0&1\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/68f40eec0dda33d6ffef4c0c25b0586470d62fef)















![{\displaystyle \mathrm {M} _{{\text{view}}\to {\text{world}}}=\left[{\begin{matrix}x_{1}&y_{1}&z_{1}&t_{1}\\x_{2}&y_{2}&z_{2}&t_{2}\\x_{3}&y_{3}&z_{3}&t_{3}\\0&0&0&1\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e00ec26b5506a084ce548aef7c370c0097ed34a)

![{\displaystyle \mathrm {M} _{{\text{view}}\to {\text{world}}}=\left[{\begin{matrix}\mathrm {R} &\mathbf {t} \\\mathbf {0} ^{T}&1\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bcd0a52a1646832fca2af268dd812f7a7cbbc5ca)

![{\displaystyle \mathrm {M} _{{\text{view}}\to {\text{world}}}^{-1}=\mathrm {M} _{{\text{world}}\to {\text{view}}}=\left[{\begin{matrix}\mathrm {R} ^{-1}&-\mathrm {R} ^{-1}\mathbf {t} \\\mathbf {0} ^{T}&1\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24280cf60fc5e0c97a0623ca0dea8a080d80b017)
![{\displaystyle \mathrm {M} _{{\text{world}}\to {\text{view}}}=\left[{\begin{matrix}\mathrm {R} ^{T}&-\mathrm {R} ^{T}\mathbf {t} \\\mathbf {0} ^{T}&1\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c67a2e4ff6d60e39d428d0cac5ab3266f5c1b586)
![{\displaystyle {\text{with }}\mathrm {R} =\left[{\begin{matrix}x_{1}&y_{1}&z_{1}\\x_{2}&y_{2}&z_{2}\\x_{3}&y_{3}&z_{3}\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ba6f143978631c3e9f3414b755a11e4429c16ee3)






![{\displaystyle \mathrm {M} _{\text{projection}}=\left[{\begin{matrix}{\frac {d}{a}}&0&0&0\\0&d&0&0\\0&0&{\frac {n+f}{n-f}}&{\frac {2nf}{n-f}}\\0&0&-1&0\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/43afae7ea0ce408c5a1a479a265177d988a0fb1c)





![{\displaystyle \mathrm {M} _{\text{projection}}=\left[{\begin{matrix}{\frac {2n}{r-l}}&0&{\frac {r+l}{r-l}}&0\\0&{\frac {2n}{t-b}}&{\frac {t+b}{t-b}}&0\\0&0&{\frac {n+f}{n-f}}&{\frac {2nf}{n-f}}\\0&0&-1&0\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/43a44af0b15159b3378c0d628f98e88f6fa82c86)
![{\displaystyle \mathrm {M} _{\text{projection}}=\left[{\begin{matrix}{\frac {2}{r-l}}&0&0&-{\frac {r+l}{r-l}}\\0&{\frac {2}{t-b}}&0&-{\frac {t+b}{t-b}}\\0&0&{\frac {-2}{f-n}}&-{\frac {f+n}{f-n}}\\0&0&0&1\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f7345d54b1caa48a201493b48d21f86f2a2321ac)




![{\displaystyle \left[{\begin{matrix}{\frac {w_{s}}{2}}&0&0&s_{x}+{\frac {w_{s}}{2}}\\0&{\frac {h_{s}}{2}}&0&s_{y}+{\frac {h_{s}}{2}}\\0&0&{\frac {f_{s}-n_{s}}{2}}&{\frac {n_{s}+f_{s}}{2}}\\0&0&0&1\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2dccc455d0d455f5128c324abe28d96a952a728d)