电路创意/在电阻薄膜上行走

<<< 目录 - 页面阶段 >>>

通过电压图"发明"各种电阻电路 （现在重现著名的欧姆实验）

电路创意：窥视一个电压供电的线性电阻器，显示电阻薄膜上的电压分布。

“发明”的器件：运动到电压转换器，分压器，电阻叠加器和减法器，反相放大器.

开始：欧姆实验

历史。 几乎三个世纪前，欧姆进行了他的著名实验。在那个黑暗时代，物理学家试图解释为什么不同导线之间存在明显的差异，什么是电流，以及它与静电之间的关系；对他们来说，电流和电压的概念是抽象的，几乎是上帝自己揭示的。正如他们所说，他拉伸了一段长度为 L、电阻为 R 的铜线；然后，他在导线上施加了电压差。由于欧姆在 19 世纪初进行了他的实验，他唯一能用作电源的只有由亚历山德罗·伏特发明的电池的前身。不幸的是，这个实验失败了，因为欧姆使用了一根电阻非常低的导线，因此电源负载过重，普通的伏特电池无法正常工作。因此，欧姆决定利用塞贝克刚刚发明的热电效应制造一个良好的电压源。因此，电压差的来源是一个热电偶；1820 年代可用的其他电源太不可靠了。欧姆将热电偶的一端浸入沸水中，另一端浸入放在三脚架上的小容器中的融化的冰中。然后，使用验电器（请记住，在那个时代他们没有 3 美元的万用表：），一块磁化针，也许还有大量的想象力，欧姆开始研究“电阻器”上的电压分布。

重现欧姆定律。 在实验室中重现欧姆实验非常有趣、激动人心和重要，因为欧姆定律是电子电路的基础，电气工程专业的学生都在学习。这是一个好主意，如果在电子课程的实践练习和理论课上，学生和老师一起重新发明一切，每一个单一元件（甚至是电阻器）。所以我们开始想象欧姆是如何做他的著名实验，并找到了电流、电压和电阻之间的基本关系。这样，现在使用现代测量仪器和毫不逊色的想象力来重现著名的欧姆实验，我们可以“发明”各种有价值的无源电阻电路。

搭建实验室装置。 为了进行欧姆的真实实验，我们需要一根电阻丝、导线、一个电源、一个电压表和一个电流表。一条总电阻为 10 Ω 的加热器上的 50 厘米长的导线充当电阻丝。绝缘铜线充当导线。一个可变电源可以产生高达 40 V/2.5 A 的电压。我们将使用两种电压表和电流表 - 老式指针式和 VOM 数字式。

水力类比：压力图

一个有分支的管道（没有流动）

让我们从考虑一个众所周知的水力类比（管道）开始 - 我们可以在周围看到它。例如，想象一个装满水的巨大容器，它供应一根细长的管道；让我们先将管道分支（图 1）。问题是：“管道内的压力是多少？”更准确地说，“沿管道的局部压力是多少？” 不会有太多人能正确地回答这些简单的问题。

我们可以了解，如果我们沿着管道等间隔钻一些小孔（如果我们想更精确，我们可以垂直地插入一些充当局部压力表的细玻璃管）。结果是我们意料之中的：所有水位（因此，沿管道的所有局部压力）都相等。这张图显示了沿管道的压力分布；我们可以将其称为“压力图”。

一个打开的管道（有流动）

现在打开管道（图 2）；水将开始流动。这是我们日常生活中众所周知的现象，有人在管道末端打开水龙头。在左侧，水压最大；在右侧，水压最小。但是现在沿管道的局部压力是多少？我们的直觉告诉我们，局部压力将从左到右逐渐减小。

实际上，水柱的高度（因此，沿管道的局部压力）从左到右逐渐减小。压力图的包络线是一个三角形。

电气领域：电压图

一个开路的电路（没有电流）

现在让我们将这些概念转移到我们的电气领域，看看沿电阻丝的电压是否以相同的方式分布。这意味着在今天的条件下重现欧姆的真实实验。

现在，将导线的两端固定在瓷绝缘端子（支架）上，先对导线的左侧施加电压（例如，10 V）（图 3）。在这种情况下，我们可以研究什么？我们用电压表测量什么？通常的观点是将电阻器视为一个点，一个没有尺寸的东西，一个只有电阻属性的两端元件。但在这里，我们有独特的机会窥视“电阻器”内部！当你沿着导线“看”时会“看到”什么？当我们从右到左滑动电压表时，它会显示什么？如果没有任何电流，沿电阻器的局部电压是多少 - 零、10 V 还是其他什么？

好吧，让我们试试。首先，将万用表的黑色测试端连接到地线。然后用红色万用表探针接触电阻丝，并沿着电阻丝移动探针，测量所有电压降（目前，相对于地线）！如果你累了，可以将鳄鱼夹夹在探针上，"咬"住电阻丝，然后沿着电阻丝移动这个"滑块"！也许，正是用这种方式，在很久以前，有人发明了真正的电位器... 无论如何，结果令人惊叹：无论鳄鱼夹在电阻膜上的哪个位置，所有局部电压都是 10V！ 显然，这个电气现象与我们上面观察到的液压现象相同：上面：连接在开路中的电阻丝上测量的局部电压相同，都等于输入电压。但是为什么呢？

记住电阻的作用 - 它"阻碍"。它阻碍什么？它阻碍、阻挡、干扰电流，通过耗散功率。但在开路中没有电流流动。因此，没有东西需要阻碍；当没有电流时，电阻不是电阻。只有当有东西需要阻碍时，电阻才是电阻！

我们可以用压力图的概念来类似地表示电阻丝上的电压分布。我们可以将电压视为一种压力；因此，我们可以用局部电压柱来表示局部电压，就像我们用局部水柱来表示局部压力一样（图 4）！与上面一样，电压柱的长度与局部电压相对于地线的幅度成正比（我们可以将零电压水平设定在电阻的高度，然后在电阻水平之上绘制正电压柱，在之下绘制负电压柱）。这些电压柱的集合构成了整个电压图。以后，为了简化图像，我们将经常使用电压图的包络线来代替电压柱的集合。

闭合电路

"发明"各种电阻器

运动到电压转换器。现在，将电阻丝的右端接地。但是要小心；电阻丝很热！看电流表 - 它显示为 1A；所以，功率为 P = V.I = V²/R = I².R = 10W。顺便问一下，这些计算正确吗（电阻值是恒定的）？我们看到，对于这根细电阻丝来说，将热量散发到环境中太困难了，它正在发热。

现在，再次沿电阻丝移动"鳄鱼滑块"，测量局部电压降；欧姆做了完全相同的事情。他将探针从一个位置移动到另一个位置，测量相应的电势，求出它们的差，并计算比值（V₂ - V₁)/(L₂ - L₁) = (V₂ - V₁)/(r₂ - r₁) = dV/dR = I。因此，他确定这个比值（即电流 I）沿电阻丝是恒定的；因此，欧姆得出结论：V/R = I。

我们可以看到，当移动"鳄鱼滑块"时，电压降从 10 伏逐渐减小到 0 伏；相应地，电压图中的柱子也会逐渐减小它们的长度（图 5）。对于任何具有某个电阻值并传递大电流到功率负载的真实导体，我们都可以绘制这样的图。

这里，输入量是什么，输出量是什么？欧里卡！以"滑块"的移动作为输入，测量电压降作为输出，我们就"发明"了传说中的（但名字错误的）电位器、运动到电压转换器、传感器... 输出量和输入量之间的关系是什么？我们"发明"的传感器是线性运动到电压转换器吗？如果是，为什么？提示：电阻沿电阻丝线性分布。好吧，根据电阻沿电阻丝线性分布这一事实，我们可以得出结论，该转换器是线性的。

在哪些地方可以看到这样的传感器？当然，最流行的应用是燃油箱液位传感器，其中浮子移动这样的电阻传感器。但是，如果你有一天打开燃油箱（小心，这很危险！），你就会发现它是非线性的。你能说出原因吗？

双极性运动到电压转换器。我们已经准备好进行更复杂的实验... 是否还有其他有趣的点（与无处不在的地线不同）可以固定负电压探针？当然，我们可以接触任何电阻丝的点！一种典型的布置是将正轨（这里为 +10V）指定为地线。但也许最有趣的点是充当地线的中间点；所以，用黑色（负极）"鳄鱼夹" "咬"住它。然后，将红色（正极）"鳄鱼夹"沿电阻丝滑动，移到黑色"鳄鱼夹"的左侧和右侧（图 6）。但是，首先用双极性万用表替换单极性万用表。为什么？我们能预期什么？结果令人惊喜：输出电压从 -5V 变化到 +5V！欧里卡！我们获得了一个双极性运动到电压传感器！当然，另一个应用是双极性可变电压源。

共模信号。让我们继续实验... 如果我们同时将两个万用表探针向同一个方向移动，会发生什么？电压没有变化。为什么？他们将这种输入称为"共模输入信号"。

差分输入信号。如果我们同时将两个万用表探针向相反方向移动，会发生什么？电压的变化速度甚至比上面更快。为什么？他们将这种输入称为"差分输入信号"。

用奇特的指示器测量电压降

我们可以使用更不寻常的指示器来测量电阻丝上的电压降，例如电灯泡（图 7）、电机、LED等。你觉得用这种奇特的方式（图 8）给电灯泡供电会有什么问题吗？如果有，什么时候以及为什么？

你知道旅行用吹风机和烤面包机利用了同样的强大理念，用低电压为其内部电路（电机、定时器等）供电吗？然后，让我们以类似的方式给一个小型的直流电机供电（图 9）。正如我们所看到的，电机速度与其速度成正比。同样，如果我们交换两个鳄鱼夹，电机会改变旋转方向（图 10）。

研究奇特的"电阻器"

铅笔石墨。如果我们有足够的创意，我们就可以研究各种不寻常的电阻材料，以观察它们上的电压分布。例如，我们可以用普通铅笔石墨上的部分电压降来给各种负载（包括 LED）供电（图 11）；这似乎是在网上非常流行的实验。^[1]

导电泡沫。另一个非传统但非常吸引人的实验是研究导电泡沫中的电压分布（图 12）。但是，这需要使用一个完美的万用表（为什么？）。但是这里的电压分布是线性的还是表面的呢？

石墨轨迹。最后，如果我们用软铅笔在纸上画一条电阻路径（铅越软，导电性越强），然后沿着这条"电阻器"滑动万用表探针，我们就可以在我们的实验中走得太远了。但你不觉得我们甚至可以测量我们人体的电压分布吗？当然，对于所有这些奇特的实验，我们需要一个非常、非常完美的（高电阻）万用表....

如何在屏幕上可视化电压图

基本思想。但是，对于我们人类来说，在电路属性（电压和电阻）变化时绘制所有电压图太难了，也太无聊了。因为这些图不能是静态的、死的图像；它们必须是"活的"图（动画），根据电路状态发生变化。因此，我们需要一台计算机，它能密切"观察"我们对被测电路的操作，并在屏幕上构建相应的"活"电压图。然后，让我们构建这样一个基于计算机的系统，让它来做这个"苦力"：）。这样，我们只需要看屏幕上的图像，并思考它背后的电路现象就行了！

组件。首先，我们需要一些计算机。它可以足够简单，只要它有一些图形功能（例如，1986 年用于在这个实验室构建 *Microlab* 系统的计算机是著名的 Apple II 的一个版本）。然后，我们只需要将一些模拟-数字转换器 (ADC) 连接到 PC 总线，它们充当模拟输入，以及一些数字-模拟转换器 (DAC) 充当模拟输出，我们的基于计算机的系统 *Microlab* 就准备好了（参见图 13）！

电源。请注意，模拟-数字外设（图 14）直接从可怜的计算机上“吸收”能量；因此，它不仅充当计算机，还为外设供电。那么，我们也可以为高电阻物体供电吗？我们能使用这些 DAC 来为被测电阻供电吗？这将允许计算机控制物体！只是，这些 DAC 的运算放大器输出只能提供最大 10 mA 电流。因此，我们无法为低电阻（10 Ω）电线供电！

电阻器。我们可以使用线性高电阻（例如，4.7 kΩ）可变电阻来代替低电阻电线。然后，我们可以使用 DAC 的 10 mA 输出为电阻器供电，没有任何问题（计算最大电流）。为了使装置更复杂，我们可以同时为电阻器两端供电。因此，将 AO1（DAC1）连接到电阻器右侧，将 AO2（DAC2）连接到电阻器左侧。

电压表。你觉得是否应该连接两个老式但吸引人的双极性电压表 V1 和 V2 来观察输入电压？或者只依赖于抽象的数字万用表和屏幕上的数字测量结果？但是，这些好用的老式仪表是“活的”、移动的、几何的、空间的和真实的；这就是人们信任它们的原因。请注意，它们也是双极性的，中间为零。但是，它们具有 20 kΩ 的内部电阻，这会有什么问题吗？提示：这两个 DAC 充当具有几乎为零输出电阻的完美电压源。

接地。现在，我们也来说说接地。但是，什么是接地？我们可以在维基百科关于虚拟接地的文章中找到可能的答案。简而言之，接地是参考点，我们根据它测量电压。复合电压源内部的任何点都可以充当真实接地（图 15）。我们使用的 PC 电源是所谓的“分体电源”。它由两个串联连接的 12 V 电源组成（- + >>> - +）。中间点在此配置中充当接地。这些 DAC 的接地内部连接到该接地。我们还必须将电压表的黑色测试端连接到该接地。

软件。现在，让我们启动一个程序，该程序可以将电压图可视化显示在屏幕上，作为“活的”动画。为此，程序使计算机“关注”三个关键点处的局部电压——电阻器左侧端点、滑块中间点和右侧端点。然后，让我们通过连接来满足它的好奇心：) 首先，将 DAC1 的输出连接到 ADC1 的输入，将 DAC2 的输出连接到 ADC2 的输入；然后，将 ADC3 的输入连接到滑块。我们可以使用键盘箭头控制这两个 DAC 的输出电压；因此，这两个 DAC 实际上充当可编程电压源。计算机持续测量三个电压（V_IN1、V_IN2 和 V_IN3），并绘制三个电压条，它们的长度与电压大小成正比。最后，它使用一条代表电压图包络的线将它们连接起来。

为了更真实，我们首先可以拆卸可变电阻器（“电位器”）并将测量探头直接接触到电阻膜。现在，我们准备继续进行这些令人惊叹的实验。我们将使用众所周知的“发明”各种设备的技术：一次只改变一个量，同时保持其他量恒定。让我们开始吧！

改变 V1：左侧控制的电压-电压转换器

上面，我们保持两个电压恒定，同时改变（移动）滑块位置；因此，我们“发明”了运动-电压转换器。但是，为什么不改变量的角色呢？

同样，我们可以将“鳄鱼滑块”停在某个地方（例如，电线中间），然后改变输入电压作为输入，就像之前一样，测量电压降（相对于接地）作为输出。因此，配置如下：我们有两个电压源；其中一个（现在是左侧的一个）变化，另一个保持恒定。计算机屏幕上的结果（图 16）令人惊叹——电压图的左端上升和下降，沿图的所有点也以减小的幅度做相同的动作（形象地说，我们可以将电压图想象成二等阿基米德杠杆）。我们可以在这种几何解释中直接看到欧姆定律

$I_{OUT}={\frac {V_{IN1}}{r1+r2}}={\frac {V_{IN1}}{R}}$

因此，我们“发明”了最简单的电压-电流转换器。但更重要的是，我们“发明”了传奇的电压分配器（电压-电压转换器或“电位器”），它在这里由左侧控制！输入电压和输出电压之间的关系是什么（所谓的“传递比”？我们可以直接从屏幕上“活”的几何解释（两个嵌套的相似三角形）中推导出它——V_OUT = V_IN1.L₂/(L₁ + L₂)。由于电阻 *r* 与长度 *L* 成正比（电阻器是线性的），我们可以得出结论

如果 V1 变化，电阻器充当左侧控制的电压-电压转换器，其传递比为 $\ Vout={\frac {r2}{r1+r2}}.Vin1$

改变 V2：右侧控制的电压-电压转换器

上面，我们“晃动”了电阻器（电压图）的左端，同时保持右端固定在零接地水平。但是，为什么不通过“移动”右端并保持左端固定在零水平来交换角色呢？让我们试试！

屏幕上的结果（图 17）并不比上面逊色——现在，电压图的右端在晃动，沿图的所有点也以与距离成正比的减小的幅度晃动。同样，我们可以将电压图想象成二等阿基米德杠杆，我们从右侧转动它。

因此，我们获得了另一个电压分配器（电压-电压转换器或“电位器”），它在这里由右侧控制。输入电压和输出电压之间的关系是什么？屏幕上“活”的几何解释（两个嵌套的相似三角形）将再次帮助我们——V_OUT = V_IN2.L₁/(L₁ + L₂)。因此，结论与上一个结论类似

如果 V2 变化，电阻器充当右侧控制的电压-电压转换器，其传递比为

$\ Vout={\frac {r1}{r1+r2}}.Vin2$

同时改变 V1 和 V2：电阻求和器

在之前的实验中，当我们改变某些输入电压时，我们保持另一个电压等于零。但是，如果我们将另一个电压保持为某个（例如，正）电压，会发生什么？更重要的是，如果我们同时改变两个电压，会发生什么？让我们先假设它们具有相同的极性。

屏幕上的结果（图 18）比之前的更令人惊叹——通过改变两个电压，我们可以将左侧和右侧的电压图抬升和下降。沿着电压图的局部电压从低电压源逐渐减小到高电压源。现在，我们可以将电压图看作一个从左侧和右侧同时转动的双面二级阿基米德杠杆。

我们现在“发明”了什么样的设备？输入电压 V_IN1、V_IN2、滑块位置 L₁/(L₁ + L₂) 和输出电压 V_OUT 之间的关系是什么？屏幕上“存在”的迷人几何解释（梯形）将再次帮助我们。如您所见，梯形的两条平行边代表两个输入电压；内部线段代表输出电压。您可能可以解决这个常见的几何学校问题（提示：画一条辅助对角线）——V_OUT = V_IN1.L₂/(L₁ + L₂) + V_IN2.L₁/(L₁ + L₂)。因此，结论与之前的结论类似。

如果两个输入电压都发生变化，则电阻器充当具有传输比的无源电阻夏季。

$\ Vout=\ {\frac {r2}{r1+r2}}.Vin1\ +{\frac {r1}{r1+r2}}.Vin2$

但这并非一个简单的夏季；如我们所见，这是一个带有加权系数的夏季。

$\ a={\frac {r2}{r1+r2}}$ 和 $\ b={\frac {r1}{r1+r2}}$

创建虚拟接地

无源电阻减法器

我们终于到达了故事中最有趣的部分……在之前的实验中，我们使用了极性相同的两个电压。但是为什么不反转一个输入源的极性呢？让我们试试吧！

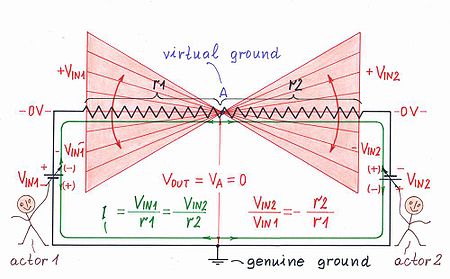
屏幕上的结果（图 19）令人惊讶且惊叹——一个电压 V_A = 0（相对于地）为零的点 A 出现在电阻膜上的某个位置！请注意，这个神秘点没有连接到真实（真实、真正的）地，但它的行为却像这样的地！这是一种人工的，虚拟接地……通常，他们在解释运算放大器电路时会介绍这个概念。但我们可以看到，这不是运算放大器电路的独特属性；它是这个只包含两个电阻的简单电阻电路的属性。从这个角度看，欧姆早在 1826 年就可能观察到虚拟接地现象，如果他只引入了一个第二个电压源！

再次，屏幕上“存在”的迷人几何解释（两个相似但现在相反的三角形）将帮助我们制定在给定点存在虚拟接地的要求。显然，两个输入电压 V_IN1 和 V_IN2 必须具有相反的极性，并且它们必须与相应的电阻 r1 和 r2（R₁ 和 R₂，如果它们代表单独的电阻）之间的比例相同： ${\frac {V_{IN2}}{V_{IN1}}}=-{\frac {r_{2}}{r_{1}}}$

如果您喜欢类比，您可以将这种安排视为一个电气“拔河”，两个电压源“相互对抗”——V_IN1“向上拉”点 A，而 V_IN2“向下拉”点 A。上拉电阻 r1 和下拉电阻 r2 在这里充当电气“绳索”。

负反馈游戏

如果我们开始改变输入电压 V_IN1 或 V_IN2 或两个电压（保持 V_IN1 = -V_IN2），会发生什么？看看，虚拟接地点左右移动！我们能把它停在电阻膜上的某个地方吗？如果我们设法把它停下来，我们将能够创建著名的带负反馈的电路……让我们试试吧！

您是否认为，与其进行枯燥的实验，不如玩一个有趣的游戏来模仿负反馈系统？如果您同意这个建议，让我们来分配角色:) 我们中的一人（“演员”1）可以扮演（成为、控制）主要独立输入电压源 V_IN1。另一个“演员”2 可以代表第二个依赖电压源 V_IN2；他/她必须保持虚拟接地不动。为此，他/她只需观察虚拟接地点（一个零指示器可能有助于测量其电压）并改变 V_IN2，以使虚拟接地电压始终等于零。

屏幕上的结果（图 20）简直太棒了！演员 1 (V_IN1) 试图移动虚拟接地点，但演员 2 (V_IN2) 将其返回到旧位置。电压图围绕固定虚拟接地点旋转，V_IN2 始终与 V_IN1 成比例；第二个电压以相反极性跟随第一个电压： $V_{IN2}=-{\frac {r_{2}}{r_{1}}}V_{IN1}$ .

真是个好主意！实际上，我们可以将输入电压 V_IN2 视为一个输出电压，并且我们可以真正地将其用作输出电压！这种安排代表了带负反馈的最简单的反相系统。

运算放大器反相放大器

如我们所见，演员 2 对这种“苦力”感到厌倦了——观察虚拟接地并改变 V_IN2:) 还有什么可以做吗？运算放大器似乎是一个不错的选择（图 21）。它具有完美的电气感；因此，它不需要零指示器来监测虚拟接地电压。同样，如果演员 1 也感到厌倦了，我们可以让计算机在 DAC1 的输出端产生一个周期性电压。好吧，我们可以看到运算放大器在数量之间保持与上述相同的比例： $V_{OA}=-{\frac {R_{2}}{R_{1}}}V_{IN}$ ；因此，我们“发明”了著名的运算放大器反相放大器！现在，我们可以通过改变滑块的位置进行一些实验：在中点，在中点的左侧和右侧。运算放大器如何对这种“干预”做出反应？电压图会发生什么变化？我们可以利用所有这些情况来构建电子电路吗？

另请参见

直流电路中的电压降
 构建并联电压求和器使用更基本的电路构建模块
虚拟接地揭示了这一著名现象的秘密

参考文献

↑ 电位器作为分压器由 Tony Kuphaldt 展示了用铅笔石墨进行有趣实验

外部链接

纸质电路 (YouTube 视频)
具有电压输出的复合无源转换器
并联电压求和器通过使用更简单的电压到电流和电流到电压转换器来构建电路 (Flash 动画；需要 Ruffle 扩展）。
我们如何创建一个虚拟接地？是关于这一伟大现象的电路故事。

<<< 顶部 - 目录 - 页面阶段 >>>

[1] 电位器作为分压器由 Tony Kuphaldt 展示了用铅笔石墨进行有趣实验