电路创意/无源电压电流转换器
电路创意: 施加在电阻器上的电压使与电阻器成比例的电流流过电阻器。

您是否注意到,在低压电子设备中,电压和电流这两个电气属性携带的是信息而不是能量?而且,由于某些原因,我们更倾向于使用电压作为数据载体?因此,大多数电子电路都具有电压输入和输出。
不幸的是 :),也存在电流输入和电流输出设备。例如:电流表只有电流输入,电流源只有电流输出,双极型晶体管具有电流输入和电流输出,电子管和场效应管具有电压输入和电流输出,跨阻放大器和诺顿放大器具有电流输入和电压输出,等等。在这些情况下,我们需要设备将携带信息的电气属性从电压转换为电流,反之亦然。
在这个故事中,我们开始揭示著名的(像欧姆定律一样)电压电流转换器的秘密,它将电气数据载体从电压更改为电流(图 1)。与往常一样,这种电路有两种版本 - 无源的(“坏的”)和有源的(“好的”)。这里,我们从“坏的”无源版本开始。然后,在另一个专门介绍“好的”有源版本的故事中,我们将展示这两个版本并非独立的。相反,这两个电路之间存在密切的相互关系:有源版本源自无源版本(有源版本包含无源版本,它只是改进的无源版本)。这样,我们将展示这个著名电路的演变,逐步地,从简单到复杂。
您是否曾经问过自己关于我们世界中因果关系的问题:“先有鸡还是先有蛋?”(困扰着从遥远的过去到现在的哲学家 :))以及,“是什么导致了什么 - 压力导致流动还是流动导致压力?” 由于我们很难回答这个基本问题,我们可能只假设两种可能的答案。
好吧,让我们首先从更流行的假设开始,即压力导致流动。实际上,我们可能会在生活中观察到很多情况,其中类似压力的量使类似流动的量通过阻碍物运动。以下是一些示例:气动(想象一个恒压泵将空气通过一个封闭的管道环路移动 - 您可以使用老式空气净化器进行这种有趣的实验,它通过由波纹软管制成的封闭环路吸入和吹出空气),水(记得著名的连通器,其中两个容器之间的高度差会导致水流动),热(如果我们在金属棒的一端加热,热量就会开始流向另一端),机械(想象一个电机驱动皮带 - 能量沿着这条“电路”流动),信息(有人给另一个人讲故事 - 数据通过电话线流动),金钱(富人给穷人钱 :)),等等。如果您需要更多示例,只需环顾四周,您就会发现很多压力导致流动(更一般地,差异导致运动)的类比。让我们最终概括所有这些情况。
如果我们对阻碍物施加压力,就会开始流动。在这种情况下,类似压力、类似流动和类似阻碍物的属性是相互关联的。通常,输出类似流动的变量与输入类似压力的变量成正比;因此,我们可以说阻碍物将类似压力的变量转换为类似流动的变量。
在电学中,我们可能会问自己上述哲学“鸡或蛋”问题的电气版本,“在欧姆定律中,是什么导致了什么 - 电压导致电流还是电流导致电压?”[1] 再次,由于我们很难回答这个基本问题,我们可能假设两种可能的答案。
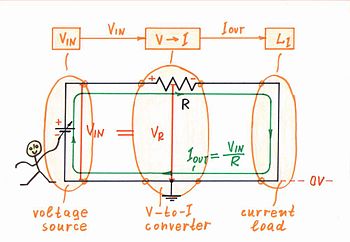
在这个故事中,我们将从更流行的假设开始,即在由电压源供电的最基本欧姆电路中,电压导致电流(图 2)。我们知道,如果我们对电阻器 R 施加电压 VIN,就会有与之成比例的电流 IOUT = VIN/R 开始流过电路。我们可以说,这是欧姆定律的电压导致电流公式:I = V/R。
在这个电压供电电路中,电阻器 R 决定流过它的电流。我们通常说电阻器将电压 VIN 转换为与之成比例的电流 IOUT,或者它用作简单的电压电流转换器 - 具有传输比 k = IOUT/VIN [mA/V] 的线性电路。
如果我们用电压条和电流环路(图 2)来可视化看不见的电气量,我们可以以比 I = V/R 更具吸引力的方式展示电路操作和欧姆定律。它们基于著名的水塔和鱼缸水力类比。在这个“几何”演示中,电压条的高度与相应的电压(降落)成正比,电流环路的厚度与电流的大小成正比(另请参见交互式动画)。
然后,我们可以用图解法来展示电路工作原理(以及欧姆定律) - 图 3。由于两个 2 端元件(电压源和电阻)上的电压和电流相同,我们可以将它们的 IV 曲线叠加到一个公共坐标系上。两条线的交点是 *工作点* A;它代表电压 VA 和电流 IA 的电流幅度。当我们改变输入电压源的电压 VIN 时,它的 IV 曲线会水平移动(参见交互式 动画)。因此,工作点 A 在电阻 R 的 IV 曲线上滑动;它的斜率代表转换器的比例。


最后,我们可以用另一种吸引人的欧姆定律图形解释 - 电压图(线性电阻内部电阻薄膜上的电压分布) - 图 4 来展示电路工作原理。在这个几何表示中,对应高度的局部条形代表局部电压降(为简单起见,我们可以只绘制电压图的包络线)。我们可以直观地从许多人类日常生活的例子中推导出电压图的概念:液压 [1]、气动、机械、热力等。这些类比有助于理解,当输入电压变化时,沿着电阻薄膜的局部电压从左到右逐渐(线性地)下降。实际上,这种安排再现了著名的欧姆实验 [2](参见另一个交互式 动画)。在这个安排中,角度 α 的正切代表电流 IOUT。
应用
[edit | edit source]充当输出设备的 V-to-I 转换器
[edit | edit source]
电压控制电流源。几乎所有自然电气来源都是恒压源(一次电池和二次电池)。实际上,自然界中不存在恒流源(除了电感器、范德格拉夫发生器和光电二极管);如果我们需要电流源,我们必须自己建造它。[2] 为此,我们将一个电压到电流转换器(电阻 R)与输入电压源 VIN 串联 - 图 5。构建公式为
电流源 = 电压源 + 电压到电流转换器
如果我们用理想电流负载(只是一根导线)短路电路输出,它将产生一个恒定电流 IOUT = VIN/R。
实际负载(图 5 上的 LED)会引入一些电压降 VL,这会影响激励电压 VIN。现在,电压差 VIN - VL 决定了电流 IOUT,而不是电压 VIN;因此,电流会减小(参见关于 缺陷 的部分)。
充当输入设备的 V-to-I 转换器
[edit | edit source]
复合电压表。电流计(检流计)实际上是电流表。为了用电流表测量电压,我们在电流表之前连接一个电压到电流转换器(称为“倍增”电阻 R)(图 6)。这样,我们可以将经典的电压表表示为由两个组件组成的复合设备
复合电压表 = 电压到电流转换器 + 电流表
经典电压表的倍增电阻充当电压到电流转换器。

复合无源转换器:类似地,在流行的电容积分器、电感微分器、对数转换器等的无源电路中,电阻充当电压到电流转换器(图 7)
V-to-V RC 积分器 = V-to-I 转换器 + I-to-V C 积分器
V-to-V RL 微分器 = V-to-I 转换器 + I-to-V L 微分器
V-to-V RD 对数转换器 = V-to-I 转换器 + I-to-V D 对数转换器
在这些电路中,相应的 I-to-V 转换器会引入一些电压降,这会影响激励电压 VIN。因此,电流会减小,并出现误差(参见关于 缺陷 的部分)。

晶体管基极电阻。BJ 晶体管是一种电流控制器件;它实际上“短路”了输入源(更准确地说,我们可以用一个小电压 VIN < VBE0 来驱动晶体管)。为了用相对较高的电压驱动晶体管(例如,在晶体管开关电路中),我们将一个基极电阻与基极-发射极结串联。它充当电压到电流转换器,从而为晶体管赋予电压输入(图 8。)
电压输入晶体管 = V-to-I 转换器 + 电流输入晶体管
出于同样的目的,电阻连接到诺顿运算放大器 [3] 的反相输入和同相输入,以便施加电压。
晶体管的基极电阻充当电压到电流转换器。

运放反相放大器(输入部分)。在运放反相电路中,运放将反相输入的电压保持在零电平(所谓的虚地)。因此,电路表现为电流控制器件,它“短路”了连接到反相输入的输入源。为了用电压驱动运放(例如,在运放反相放大器电路中),我们在输入电压源和反相输入之间连接一个电阻,该电阻充当电压到电流转换器(图 9)
运放反相放大器 = V-to-I 转换器 + 运放 I-to-V 转换器
运放 V-to-V RC 积分器 = V-to-I 转换器 + 运放 I-to-V C 积分器
运放 V-to-V RL 微分器 = V-to-I 转换器 + 运放 I-to-V L 微分器
运放 V-to-V RD 对数转换器 = V-to-I 转换器 + 运放 I-to-V D 对数转换器
输入/输出电阻是多少?
[edit | edit source]
研究输入电阻和输出电阻很有趣(为了具体起见,假设负载电阻为 RL)。
输入电阻。首先,将电流表 *串联到* 转换器输入,并将电压表 *并联到* 转换器输入;然后,改变输入电压以研究输入电阻。从输入源一侧看,我们看到两个串联的电阻;因此,输入电阻为 RIN = R + RL。如你所见,它取决于负载电阻 RL。

输出电阻。现在,将电压表 *并联到* 转换器输出,并将电流表 *串联到* 转换器输出;然后,改变负载电阻(电压)并观察电流以研究输出电阻。从负载一侧看,我们只看到电阻 R;因此,输出电阻为 ROUT = R。这里我们假设输入电压源是完美的(即,它的内部电阻为零)。
缺陷
[edit | edit source]
实际负载充当不完美的电流负载,消散能量(例如,简单的电流表、电流测量电阻、二极管等)或存储能量(电容器、二次电池、电感器等)。它们具有一定的电阻(线性或非线性)、电容或电感,会导致负载上出现电压降 VL(图 12)。因此,现在电压差 VIN - VL 决定了电流 IOUT,而不是仅由电压 VIN 决定;因此,电流会减小。如果你点击交互式 Flash 电影 [3] 中的 *探索* 按钮,或者如果你转到交互式 Flash 构建器 中的 *阶段 2*,你可以以更具吸引力的方式探索电路工作原理。[4]
在 连通器 的水流比喻中也存在同样的问题,其中容器之间的高度差决定了流速,而不是仅由输入水压源的高度来决定。
经典补救措施。 在某些情况下(例如,当无源电压到电流转换器是电流源的一部分时),我们可能会从日常生活中运用一种自相矛盾的技巧——用另一个大得多的有害数量来贬低一个有害数量。在电力中,这是降低负载引起的误差的众所周知的经典补救措施:增加励磁电压 V 和电阻 R 以抑制负载电压降 VL。结果,输出电流保持不变,但负载的影响(即使它变化)也会减小;因此,我们得到一个相对恒定的电流源。如果我们走得太远,我们将“发明”经典的“电力”定义中的理想电流源,其中无限电压除以无限电阻得到有限电流。例如,想象一下,我们首先使用 10V 电压源和 10K 电阻构建一个 1mA 电流源,然后使用 100V 和 100K,然后使用 1000V 和 1000K,……最后使用无限 V 和无限 K。只想象一下该电阻在这种折衷方案中将消耗多少功率!此外,我们通常无法改变输入电压 V 和电阻 R。那么如何解决这个问题呢?
寻找完美的补救措施。 注意,在简单的电压到电流转换器中存在一个奇怪的矛盾:一方面,电压降 VL 很有用,因为它用作输出电压;另一方面,这种电压降是有害的,因为它会降低流过电阻 R 的实际产生电流的电压 VR。我们如何解决这种矛盾?记住,当生活中出现不好的事情时我们会怎么做。如果你找不到补救措施,请访问有关 有源电压到电流转换器 的相关故事,以获得答案。
无源电压到电流转换器不像相反的 无源电流到电压转换器 那样流行。实际上,它存在于几乎所有基本电子学书籍中,但作者并没有区分它。结果,很少有资源明确地展示它,而是隐含地展示它。以下是一些资源。
- ↑ 具有电流输出的基本无源转换器 是关于最简单电力转换器的教师故事。
- ↑ 重新发明恒流源 揭示了恒流源的原理。
- ↑ 无源电压到电流转换器 是一个动画 Flash 教程,揭示了无源版本的原理。
- ↑ 运放电路构建器 (电影理念) 是一个交互式 Flash 教程,展示了如何将任何无源转换器转换为有源转换器(从右侧库中选择电阻 R2 以构建电压到电流转换器)。
重新发明运放反相电压到电流转换器 揭示了有源版本背后的基本原理。
无源电流到电压转换器 将揭示“镜像”电路无源版本背后的基本原理。
电阻器 是关于最简单的电阻元件的综合故事。
电压到电流转换器 介绍了电路的无源和有源版本。
电流到电压转换器 介绍了“镜像”电路的无源和有源版本。
重新发明电压到电流转换器 是一个类似的电路故事,但它结构更好,更容易浏览。
无源电压到电流转换器 是一个交互式 Flash 电影(需要 Flash 播放器)
电压表设计 对普通的“运动”电压表提出了一个经典但有用的观点。
