电路理论/双源激励/戴维南和诺顿

戴维南电压

• 
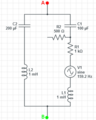
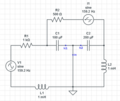
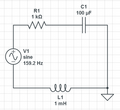
  移除负载电阻R₃
• 
  向上和向下重绘
• 
  打开电流源（使用叠加法）
• 
  短路电压源（使用叠加法）

打开电流源后，得到一个串联电路。总电流将是 

$\mathbb {I} _{t}={\frac {\mathbb {V} _{s}}{X_{L1}+X_{L2}+R_{1}+X_{C2}+X_{C1}}}$

由电压源产生的V_AB将是C2和L2之间的压降，即（matlab代码）

$\mathbb {V} _{AB}=\mathbb {I} _{t}*(-4j)=0.0204-0.0344*i$

由电流源产生的V_AB稍微复杂。在C₂和L₂之间接地。在C₁、R₂和R₁的连接点进行节点分析

$\mathbb {I} _{S}-{\frac {\mathbb {V} _{N}}{R_{1}+X_{L1}+X_{L2}}}-{\frac {\mathbb {V} _{N}}{X_{C1}+X_{C2}}}=0$

求解V_N

$\mathbb {V} _{N}=\mathbb {I} _{S}{\frac {1}{{\frac {1}{R_{1}+X_{L1}+X_{L2}}}+{\frac {1}{X_{C1}+X_{C2}}}}}$

现在可以找到两个并联支路的电流。然后V_AB将是C₂的压降减去L₂的压降（因为电流方向相反）

$V_{AB}={\frac {\mathbb {V} _{N}}{X_{c1}+X_{C2}}}*X_{C2}-{\frac {\mathbb {V} _{N}}{R_{1}+X_{L1}+X_{L2}}}*X_{L2}=118.0-118.0*i$

因此，戴维南电压将是两个V_AB的总和（matlab代码）

$V_{th}=118.0-118.0*i$

诺顿电流

• 
  负载电阻R₃短路，诺顿电流被识别
• 
  打开电流源（使用叠加法计算）
• 
  短路电压源（使用叠加法计算）

电压源短路时的短路电流即为总电流

$\mathbb {I} _{N}={\frac {\mathbb {V} _{1}}{R_{1}+X_{C1}+X_{L1}}}$

由于电流源导致的短路电流稍微复杂一点。从第一个图可以看出

$\mathbb {I} _{N}=\mathbb {I} _{C}1-\mathbb {I} _{C}2$

I_C1 和 I_C2 都可以通过电流分配器找到，因此 I_N 为

$\mathbb {I} _{N}=\mathbb {I} _{s}*({\frac {R1+X_{L1}}{R1+X_{L1}+X_{C1}}}-{\frac {X_{L2}}{X_{L2}+X_{C2}}})$