电路理论/模拟计算机

目标

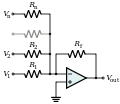
设计一个模拟计算机，用于生成以下微分方程的解

$a_{2}{d^{2}v(t) \over dt^{2}}+a_{1}{dv(t) \over dt}+a_{o}v(t)=f(t)$

f(t) 是输入，即汽车经过的颠簸

v(t) 是输出，即汽车对颠簸的垂直运动

a₂ 与减震器的弹簧常数有关

a₁ 与阻尼系数和油的粘度有关

a_o 根据所需的乘坐感受而变化

目标是通过电子方式改变 a₂、a₁ 和 a_o，而不是实际构建多个模型。这就像二战前所做的建模，而不是使用 matlab 或类似软件。

现代应用包括控制系统（工业过程中的阀门开闭、电机开闭、核电站控制）。

组织

乍一看，需要 6 个运算放大器，2 个用于微分，3 个用于缩放，1 个用于加法。

但加法器也可以进行缩放。

还需要考虑整体电路设计。期望的输出是 v(t)。函数 f(t) 是输入。导数是通过反馈输出构建的临时值。所以数学公式看起来像这样

${\frac {a_{2}}{a_{o}}}{d^{2}v(t) \over dt^{2}}+{\frac {a_{1}}{a_{o}}}{dv(t) \over dt}-{\frac {1}{a_{o}}}f(t)=v(t)$

还需要将输出反馈到输入...并将先求一阶导数，再求二阶导数，然后与 f(t) 一起馈送到加法器。所以数学公式看起来更像这样

$-(-{\frac {a_{1}}{a_{o}}}{dv(t) \over dt}-{\frac {a_{2}}{a_{o}}}{d^{2}v(t) \over dt^{2}}+{\frac {1}{a_{o}}}f(t))=v(t)$

• 
  这将输入进行微分，因此输出为 $-{dv(t) \over dt}$
• 
  这将第一个导数的输出（为负值）变为正值，因此第二个导数也将为负值
• 
  这将生成二阶导数 ${d^{2}v(t) \over dt^{2}}$，现在它与第一个导数一样为负值
• 
  这将获取负值 ${dv(t) \over dt}$ 和负值（因为被反转了） $-{d^{2}v(t) \over dt^{2}}$ 项，并将它们添加到正值 f(t) 中，并进行适当的缩放以生成 $v(t)$

模拟

假设 OA4 的输出是 v(t)。

那么 OA1 的输出是

$-R_{1}C_{1}{dv(t) \over dt}$

OA2 的输出是

$-{\frac {R_{3}}{R_{2}}}(-R_{1}C_{1}{dv(t) \over dt})={\frac {R_{3}R_{1}}{R_{2}}}C_{1}{dv(t) \over dt}$

OA3 的输出为

$-R_{4}C_{2}{d({\frac {R_{3}R_{1}}{R_{2}}}C_{1}{dv(t) \over dt}) \over dt}=-{\frac {R_{4}R_{3}R_{1}}{R_{2}}}C_{1}C_{2}{d^{2}v(t) \over dt^{2}}$

假设 V₁₄ 为 f(t)，那么 OA4 的输出，即加法器的输出为

$-R_{8}({\frac {f(t)}{R_{7}}}+{\frac {-{\frac {R_{4}R_{3}R_{1}}{R_{2}}}C_{1}C_{2}{d^{2}v(t) \over dt^{2}}}{R_{5}}}+{\frac {-R_{1}C_{1}{dv(t) \over dt}}{R_{56}}})={\frac {R_{8}R_{1}}{R_{56}}}C_{1}{dv(t) \over dt}+{\frac {R_{8}R_{4}R_{3}R_{1}}{R_{5}R_{2}}}C_{1}C_{2}{d^{2}v(t) \over dt^{2}}-{\frac {R_{8}}{R_{7}}}f(t)$

将此与

${\frac {a_{1}}{a_{o}}}{dv(t) \over dt}+{\frac {a_{2}}{a_{o}}}{d^{2}v(t) \over dt^{2}}-{\frac {1}{a_{o}}}f(t)=v(t)$

可以看出

${\frac {a_{1}}{a_{0}}}={\frac {R_{8}R_{1}}{R_{56}}}C_{1}$

${\frac {a_{2}}{a_{o}}}={\frac {R_{8}R_{4}R_{3}R_{1}}{R_{5}R_{2}}}C_{1}C_{2}$

${\frac {1}{a_{0}}}={\frac {R_{8}}{R_{7}}}$

已知 a₀、a₁ 和 a₂ 三个已知数，10 个未知数和 3 个方程。因此，问题是约束不足的，这意味着可以使用其他要求来选择电阻和电容值。