电路理论/分析方法

电路理论

分析方法

当电路变得庞大而复杂时，拥有各种简化和分析电路的方法将非常有用。没有完美的公式来解决电路问题。根据电路的类型，可以采用不同的方法来解决电路。某些方法可能无效，而某些方法在涉及复杂数学运算时可能非常困难。解决电路的两个最重要方法是节点分析法和网孔电流分析法。这些方法将在下面进行解释。

叠加

电路分析领域最重要的原则之一是叠加原则。它仅对线性电路有效。

叠加原理指出，多个贡献源对线性电路的总效应等于每个源单独作用时的效应之和。

这意味着什么？用通俗的语言来说，这意味着如果我们有一个具有多个源的电路，我们可以一次“关闭”除一个源之外的所有源，然后仅用一个源激活的情况下研究电路。我们对每个源依次进行此操作，然后将每个源的效应加在一起得到总效应。在我们使用此原理之前，我们必须了解其背后的数学基础。

必要条件

叠加只能应用于线性电路；也就是说，电路中所有源与电路响应之间都存在线性关系。仅使用几个代数规则，我们可以构建叠加的数学理解。如果f表示响应，a和b是常数，那么

f(ax_{1}+bx_{2})=f(ax_{1})+f(bx_{2})\,

就电路而言，它清楚地解释了叠加的概念；每个输入可以单独考虑，然后相加得到输出。通过几个额外的代数性质，我们可以看到叠加不能应用于非线性电路。在这个例子中，响应y等于输入x的平方，即 y=x²。如果a和b是常数，那么

y=(ax_{1}+bx_{2})^{2}\neq (ax_{1})^{2}+(bx_{2})^{2}=y_{1}+y_{2}\,

请注意，这只是无限多个反例之一……

逐步操作

使用叠加法来找到给定的输出可以分解为四个步骤

隔离一个源 - 选择一个源，并将所有剩余的源设置为零。在开路和闭路电路中解释了“关闭”这些源的后果。总而言之，关闭电压源会导致短路，关闭电流源会导致开路。（原因 - 无法通过开路流动电流，短路之间没有压降。）
找到来自隔离源的输出 - 一旦隔离了一个源，可以使用我们到目前为止学习的任何技术来找到该源的响应。
对每个源重复步骤1和2 - 继续选择一个源，将剩余的源设置为零，然后找到响应。重复此过程，直到考虑了所有源。
将输出相加 - 一旦找到每个源导致的输出，将它们加在一起即可找到总响应。

冲激响应

可以利用电路的冲激响应来确定电路的输出。

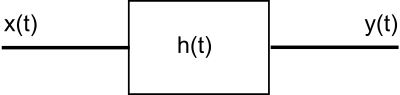
输出 y 是输入 x 与冲激响应的卷积 h * x。

[卷积]

y(t)=(h*x)(t)=\int _{-\infty }^{+\infty }h(t-s)x(s)ds

.

如果输入 x(t) 是冲激 ( $\delta (t)$ )，输出 y(t) 将等于 h(t)。

通过了解电路的冲激响应，可以将任何源插入电路，然后通过卷积计算输出。

卷积

卷积运算是一个非常困难且复杂的运算，它将两个方程组合成一个结果方程。卷积的定义基于定积分，因此求解卷积方程需要积分微积分的知识。本维基教科书不需要读者事先了解积分微积分，因此不会深入讨论这个主题，只提供简单的定义和一些解释。

定义

两个函数 a 和 b 的卷积 a * b 定义为

(a*b)(t)=\int _{-\infty }^{\infty }a(\tau )b(t-\tau )d\tau

记住
星号表示卷积，而不是乘法

星号运算符用于表示卷积。许多计算机系统和经常在计算机上写数学的人通常使用星号表示简单的乘法（星号是许多编程语言中的乘法运算符），但在这里必须做出重要的区分：星号运算符表示卷积。

性质

卷积是可交换的，也就是说 $a*b=b*a$ 。卷积也对加法是分配的，即 $a*(b+c)=a*b+a*c$ ，并且是结合的，即 $a*(b*c)=(a*b)*c$ .

系统和卷积

假设我们有以下的框图系统

	x(t) = 系统输入 h(t) = 冲激响应 y(t) = 系统输出

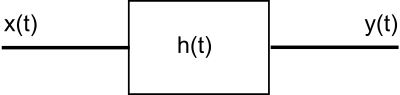其中 x(t) 是电路的输入，h(t) 是电路的冲激响应，y(t) 是输出。在这里，我们可以通过将冲激响应与电路的输入进行卷积来找到输出。因此，我们看到电路的冲激响应不仅仅是输出与输入的比率。然而，在频域中，输出中频率为 ω 的分量是输入中具有相同频率的分量与该频率下传递函数的乘积。故事的寓意是：电路的输出是输入与冲激响应的卷积。