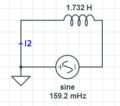
串联元件可以合并在一起.. 这简化了电路。
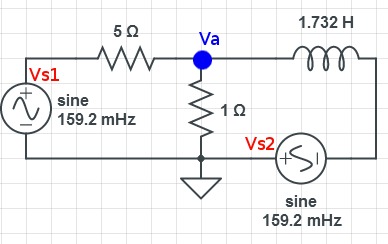
文件:Example70mupad.pngmupad 和 matlab 代码 用于以下所有工作





求解

这与通过 1 欧姆电阻的电压相同。
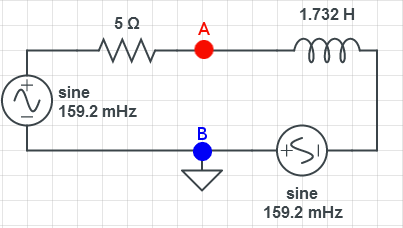
使接地成为  的负极,然后
的负极,然后



求解

-
将负载短路
-
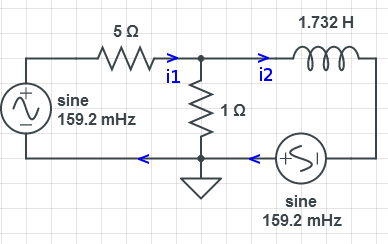
将电路分为两个部分,以便使用叠加原理
-
通过短路电压源,使电路的一半短路



将电压源短路,将电流源开路,移除负载并找到负载连接处的阻抗

检查

是的!它们匹配

将找到电阻中的电流并与网状电流进行比较

是的!它们匹配



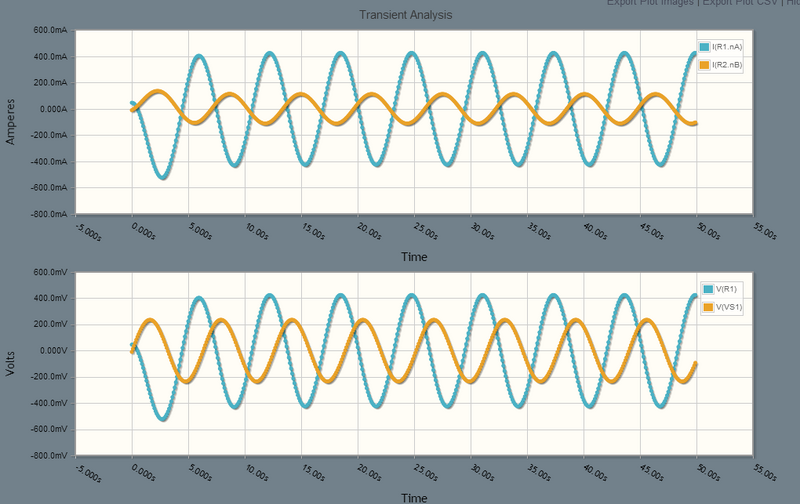
该电路已经仿真。 找到了一种将方程式输入电压源参数的方法,可以提高精度
-
输入 sqrt(3) 而不是数值近似值
-
添加 pi/2 以从 cos 转换为 sin 源
要与上述结果进行比较,需要将电阻器上的电流和电压转换为时域。
周期看起来大约是 6 秒... 应该是

通过 1 欧姆电阻的电流,一旦被移动到时域(从上面的数字),就是

从网孔分析,计算了两个电源的电流

幅值是准确的,它们几乎相差 π,这可以在模拟中看到。
电压与通过 1 欧姆电阻的电流相同

第一个(左侧)电源的电压为

幅值匹配。 由于第一个电源看到了电感器,电源的电压在电流之前达到峰值。
电阻器的电压应该在电源之前达到峰值 171 - 45 = 126°... 似乎它确实如此。