电路理论/拉普拉斯变换

拉普拉斯变换

拉普拉斯变换是一种强大的工具，在电气工程中非常有用。该变换允许将“时域”中的方程转换为复数 s 域中等效的方程。拉普拉斯变换是一种积分变换，虽然读者不需要了解积分微积分，因为所有结果都将提供。本页面将讨论拉普拉斯变换，它只是一种用于求解和操作常微分方程的工具。

电路元件的拉普拉斯变换类似于相量表示，但它们并不相同。拉普拉斯变换比相量更通用，并且在某些情况下更容易使用。此外，不要将“复数 s 域”与我们之前讨论过的复功率概念混淆。复功率使用变量$\mathbb {S}$，而拉普拉斯变换使用变量 s。拉普拉斯变量 s 与功率无关。

该变换以数学家皮埃尔·西蒙·拉普拉斯（1749-1827）的名字命名。该变换本身直到奥利弗·亥维赛德，一位著名的电气工程师，开始使用它的变体来求解电路才变得流行。

拉普拉斯域

拉普拉斯域，或“复数 s 域”，是拉普拉斯变换将时域方程变换到的域。s 是一个复变量，由实部和虚部组成

$s=\sigma +j\omega$

拉普拉斯域将实部 (σ) 作为横轴，将虚部 (ω) 作为纵轴。s 的实部和虚部可以被视为独立量。

此符号与傅立叶变换理论中使用的符号的相似之处并非巧合；对于$\sigma =0$，如果信号是因果的，则拉普拉斯变换与傅立叶变换相同。

变换

拉普拉斯变换的数学定义如下

[拉普拉斯变换]

$F(s)={\mathcal {L}}\left\{f(t)\right\}=\int _{0^{-}}^{\infty }e^{-st}f(t)\,dt$

注意
字母s没有特殊含义，在拉普拉斯变换中使用它是作为一种常见约定。

变换，通过定积分，消除了结果方程中的所有 t，而是留下新的变量 s，它是一个复数，通常写成$s=\sigma +j\omega$。本质上，该变换取函数 f(t)，并将其“变换”为关于 s 的函数 F(s)。一般来说，函数 f(t) 的变换写成 F(s)。时域函数用小写字母表示，而结果的 s 域函数用大写字母表示。

在
附录中

有一个拉普拉斯变换对的表格，我们将使用以下符号来显示函数的变换

$f(t)\Leftrightarrow F(s)$

我们使用这种符号，因为我们可以使用拉普拉斯逆变换将 F(s) 转换回 f(t)。

逆变换

拉普拉斯逆变换将复数 S 域中的函数转换为其在时域中的对应函数。它的数学定义如下

[拉普拉斯逆变换]

${\mathcal {L}}^{-1}\left\{F(s)\right\}={1 \over {2\pi }}\int _{c-i\infty }^{c+i\infty }e^{ft}F(s)\,ds=f(t)$

其中 $c$ 是一个实常数，使得所有极点 $s_{1},s_{2},...,s_{n}$ of $F(s)$ 位于区域 ${\mathfrak {R}}\{s_{i}\}<c$ 中。换句话说，$c$ 的选择使得 $F(s)$ 的所有极点都在与实轴在 $s=c$ 处相交的垂直线左侧。

逆变换在数学上比变换本身更困难。然而，幸运的是，拉普拉斯变换及其逆变换的广泛表格已经计算出来，并且可以方便地浏览。

变换性质

拉普拉斯变换性质表在
附录

拉普拉斯变换最重要的性质（目前）如下

${\mathcal {L}}\left\{f'(t)\right\}=sF(s)-f(0)$

类似地，我们可以用类似的方式表达高阶导数

${\mathcal {L}}\left\{f''(t)\right\}=s^{2}F(s)-sf(0)-f'(0)$

或者对于任意导数

${\mathcal {L}}\left\{f^{(n)}(t)\right\}=s^{n}F(s)-\sum _{i=0}^{n-1}s^{(n-1-i)}f^{(i)}(0)$

其中符号 $f^{(n)}(t)$ 表示函数 $f$ 在点 $t$ 处的 n 次导数，而 $f^{(0)}(t)$ 表示 $f(t)$.

通俗地说，拉普拉斯变换将微分运算转化为多项式运算。唯一需要记住的重要一点是，我们必须添加时域函数的初始条件，但对于大多数电路，初始条件为 0，因此我们不需要添加任何东西。

对于积分，我们得到以下结果

${\mathcal {L}}\left\{\int _{0}^{t}f(t)\,dt\right\}={1 \over s}F(s)$

初始值定理

拉普拉斯变换的**初始值定理**如下所示：

[初始值定理]

$f(0)\Leftrightarrow \lim _{s\to \infty }sF(s)$

这对于求解微分运算变换时所需的函数初始条件很有用（见上文）。

最终值定理

与初始值定理类似，**最终值定理**指出，我们可以找到函数 f 在 t 趋于无穷大时的值，在拉普拉斯域中，如下所示：

[最终值定理]

$\lim _{t\to \infty }f(t)\Leftrightarrow \lim _{s\to 0}sF(s)$

这对于求解电路的稳态响应很有用。最终值定理只能应用于稳定系统。

传递函数

如果我们有一个在时域中具有脉冲响应 h(t) 的电路，输入为 x(t)，输出为 y(t)，我们可以通过变换所有三个元素来找到电路在拉普拉斯域中的**传递函数**。

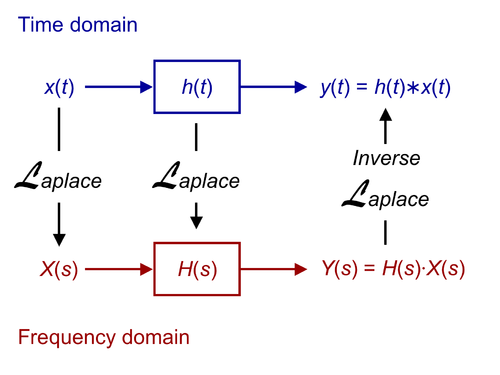
在这种情况下，H(s) 被称为电路的“传递函数”。它可以定义为脉冲响应的变换，也可以定义为电路输出与其在拉普拉斯域中的输入的比值。

[传递函数]

$H(s)={\mathcal {L}}\left\{h(t)\right\}={\frac {Y(s)}{X(s)}}$

传递函数是分析电路的强大工具。如果我们知道电路的传递函数，那么我们就掌握了理解电路所需的所有信息，而且我们拥有了一种易于操作的形式。当我们获得传递函数时，就可以说电路已完全“解决”。

卷积定理

之前提到过，我们可以通过使用卷积运算来计算系统的输出，该输出来自输入和脉冲响应。作为提醒，给定以下系统：

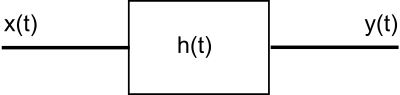
x(t) = 系统输入 h(t) = 脉冲响应 y(t) = 系统输出

我们可以使用卷积运算来计算输出，如下所示：

$y(t)=x(t)*h(t)$

其中星号表示卷积，而不是乘法。但是，在 S 域中，由于拉普拉斯变换的一个特性，此运算变得容易得多。

[卷积定理]

${\mathcal {L}}\left\{a(t)*b(t)\right\}=A(s)B(s)$

其中星号运算符表示卷积运算。这使我们得到了卷积定理的英文表述：

时域中的卷积在 S 域中变为乘法，S 域中的卷积在时域中变为乘法。

现在，如果我们在拉普拉斯 S 域中有一个系统

X(s) = 输入 H(s) = 传递函数 Y(s) = 输出

我们可以从输入 X(s) 和传递函数 H(s) 计算输出 Y(s)

$Y(s)=X(s)H(s)$

注意，此属性与相量非常相似，其中可以通过将输入乘以网络函数来确定输出。因此，网络函数和传递函数是非常相似的量。

电阻

拉普拉斯变换可以独立地应用于不同的电路元件，然后可以在 S 域中完全求解电路（这更容易）。让我们看看一些电路元件

电阻是时间和频率不变的。因此，电阻的变换与电阻本身的阻值相同

[电阻变换]

$R(s)=r$

将此结果与电阻 r 的相量阻抗值进行比较

$Z_{r}=r\angle 0$

您可以很快地看到，相量和拉普拉斯变换之间的阻值非常相似。

欧姆定律

如果我们将欧姆定律进行变换，我们将得到以下方程式

[欧姆定律变换]

$V(s)=I(s)R$

现在，根据欧姆定律，电路元件的电阻是电压与电流的比值。因此，我们将求解量 ${\frac {V(s)}{I(s)}}$，结果将是我们的电路元件的电阻

$R={\frac {V(s)}{I(s)}}$

这个比值，即电阻的输入/输出比值，是一个重要的量，我们将为所有电路元件找到这个量。我们可以说，阻值为 r 的电阻的变换由下式给出

[电阻变换]

${\mathcal {L}}\{{\text{resistor}}\}=R=r$

电容器

让我们看一下时间域中电压、电流和电容之间的关系

$i(t)=C{\frac {dv(t)}{dt}}$

求解电压，我们得到以下积分

$v(t)={\frac {1}{C}}\int _{t_{0}}^{\infty }i(t)dt$

然后，将这个方程变换到拉普拉斯域，我们得到以下结果

$V(s)={\frac {1}{C}}{\frac {1}{s}}I(s)$

同样，如果我们求解比值 ${\frac {V(s)}{I(s)}}$，我们将得到以下结果

${\frac {V(s)}{I(s)}}={\frac {1}{sC}}$

因此，电容为 C 的电容器的变换由下式给出

[电容器变换]

${\mathcal {L}}\{{\mbox{capacitor}}\}={\frac {1}{sC}}$

电感器

让我们看看电感的方程式

$v(t)=L{\frac {di(t)}{dt}}$

将其代入拉普拉斯域，我们得到以下公式

$V(s)=sLI(s)$

求解比值 ${\frac {V(s)}{I(s)}}$，我们得到以下结果

${\frac {V(s)}{I(s)}}=sL$

因此，电感为 L 的电感器的变换由以下给出

[电感器的变换]

${\mathcal {L}}\{{\text{inductor}}\}=sL$

阻抗

由于所有负载元件可以合并成一个依赖于 s 的单一格式，因此我们将所有负载元件的效果称为阻抗，与我们在相量表示中所称的一样。我们用大写字母 Z 表示阻抗值（但不表示相量 $\mathbb {Z}$）。

确定电路中的电流

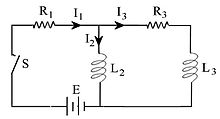电容为零、初始电流为零的 RCL 电路。

在所示网络中，假设每个电流在开关闭合时均为零，确定电流 $I_{1}(t)$、$I_{2}(t)$ 和 $I_{3}(t)$ 的性质。

解

电路中结点的电流流动

由于任何结点处电流的代数和为零，因此

$I_{1}(t)-I_{2}(t)-I_{3}(t)=0$.........(182)

电路上的电压平衡

将电压定律应用于左侧的电路，我们得到

$I_{1}(t)R_{1}+L_{2}{\frac {dI_{2}(t)}{dt}}\ =E(t)$......... (182-1)

再次将电压定律应用于外部电路，考虑到 E 是恒定的，我们得到

$I_{1}(t)R_{1}+I_{3}(t)R_{3}+L_{3}{\frac {dI_{3}(t)}{dt}}\ =E(t)$......... (182-2)

电流和电压方程的拉普拉斯变换

对 (182)、(182-1) 和 (182-2) 进行拉普拉斯变换，我们得到

$i_{1}(s)-i_{2}(s)-i_{3}(s)=0$.........(182-3)

$i_{1}(s)R_{1}+sL_{2}i_{2}(s)={\frac {E}{s}}\$......... (182-4)

$i_{1}(s)R_{1}+(R_{3}+sL_{3})i_{3}(s)={\frac {E}{s}}\$ ......... (182-5)

拉普拉斯变换的实现回顾

三个拉普拉斯变换后的方程 (182-3)、(182-4) 和 (182-5) 展示了 积分变换将微分方程转换为线性代数方程的优势，可以求解这些方程以获得因变量（在本例中为三个电流），然后进行逆变换以得到所需的解。

• 在方程 (182-3) 中，我们利用了拉普拉斯变换的 *求和性质*。
• 在方程 (182-4) 中，我们利用了 *微分导数* 的变换，如下所示。

$si_{2}(s)-I_{2}(0)={\mathcal {L}}\left\lbrace {\frac {dI_{2}}{dt}}\right\rbrace$.........(182-4.1)

由于给定的初始条件替代为：$I_{2}(0)=0$

• 在方程 (182-5) 中，我们也利用了微分导数的变换

$si_{3}(s)-I_{3}(0)={\mathcal {L}}\left\lbrace {\frac {dI_{3}}{dt}}\right\rbrace$.........(182-5.2)

同样，我们用给定的初始条件替代：$I_{3}(0)=0$

施加的电压是阶跃函数这一事实表明使用了阶跃函数的拉普拉斯变换，如下所示

${\frac {E}{s}}={\mathcal {L}}\left\lbrace E\right\rbrace$.........(182-5.3)

求解线性联立方程

三个线性联立方程（182-3）、（182-4）和（182-5）有三个未知数 $i_{1}(s)$，$i_{2}(s)$和$i_{3}(s)$，可以通过克莱姆法则等简单的消元方法求解，如下。

$i_{1}(s)={\frac {\begin{vmatrix}0&-1&-1\\{\frac {E}{s}}\ &sL_{2}&0\\{\frac {E}{s}}\ &0&R_{3}+sL_{3}\\\end{vmatrix}}{\Delta }}={\frac {E}{s}}{\frac {R_{3}+s(L_{2}+L_{3})}{\Delta }}$ ......... (182-6)

其中，矩阵的行列式 ∆ 如下确定

$\Delta ={\begin{vmatrix}1&-1&-1\\R_{1}&sL_{2}&0\\R_{1}&0&R_{3}+sL_{3}\\\end{vmatrix}}={\begin{vmatrix}1&0&0\\R_{1}&sL_{2}+R_{1}&R_{1}\\R_{1}&R_{1}&R_{1}+R_{3}+sL_{3}\\\end{vmatrix}}$

$\Delta =s^{2}L_{2}L_{3}+s(R_{1}L_{2}+R_{3}L_{2}+R_{1}R_{3})+R_{1}R_{3}$......... (182-6.1)

由于我们对 ∆ 的因式感兴趣，我们考虑方程 ∆ = 0。由于这个方程的所有系数都是正数，因此它不可能有正根。它的判别式为

$(R_{1}L_{2}+R_{3}L_{2}+R_{1}R_{3})^{2}-4L_{2}L_{3}R_{1}R_{3}$ ........ (182-6.1.1)

可以写成

$R_{1}^{2}L_{2}^{2}+2R_{1}L_{2}(R_{3}L_{2}+R_{1}L_{3})+(R_{3}L_{2}-R_{1}L_{3})^{2}$........ (182-6.1.2)

这是一个正数。因此方程 Δ = 0 具有两个不同的负根 $-\alpha _{1}$ 和 $-\alpha _{2}$，假设。

因此，

$\Delta =L_{2}L_{3}(s+\alpha _{1})(s+\alpha _{2})$ ......... (182-6.2)

其中，$-\alpha _{1}$ 和 $-\alpha _{2}$ 是二次方程 (182-6.1) 的根，如下所示：

$\alpha _{1}={\frac {1}{2}}\left\lbrace {\frac {R_{1}L_{2}+R_{3}L_{2}+R_{1}R_{3}}{L_{2}L_{3}}}+{\sqrt {\left({\frac {R_{1}L_{2}+R_{3}L_{2}+R_{1}R_{3}}{L_{2}L_{3}}}\right)^{2}-4{\frac {R_{1}R_{3}}{L_{2}L_{3}}}}}\right\rbrace$ ......... (182-6.2.1)

$\alpha _{2}={\frac {1}{2}}\left\lbrace {\frac {R_{1}L_{2}+R_{3}L_{2}+R_{1}R_{3}}{L_{2}L_{3}}}-{\sqrt {\left({\frac {R_{1}L_{2}+R_{3}L_{2}+R_{1}R_{3}}{L_{2}L_{3}}}\right)^{2}-4{\frac {R_{1}R_{3}}{L_{2}L_{3}}}}}\right\rbrace$ ......... (182-6.2.2)

因此，方程 (182-6) 和 (186-6.2) 给出

$i_{1}(s)={\frac {E}{s}}.{\frac {R_{3}+s(L_{2}+L_{3})}{L_{2}L_{3}(s+\alpha _{1})(s+\alpha _{2})}}$

$i_{1}(s)={\frac {A_{0}}{s}}+{\frac {A_{1}}{s+\alpha _{1}}}+{\frac {A_{1}}{s+\alpha _{2}}}$ .........(182-7)

常数 $A_{0}$, $A_{1}$, 和 $A_{2}$ 是用 $R_{1}$, $L_{2}$, $L_{3}$, 和 $R_{3}$ 表示的，给出如下：

$A_{0}=-{\frac {ER_{3}}{L_{2}L_{3}\alpha _{1}\alpha _{2}}}$ .........(182-7.1)

$A_{1}=E{\frac {R_{3}\alpha _{2}-\alpha _{1}\alpha _{2}(L_{2}+L_{3})}{L_{2}L_{3}\alpha _{1}\alpha _{2}(\alpha _{1}-\alpha _{2})}}$.........(182-7.2)

$A_{2}=E{\frac {\alpha _{2}(L_{2}+L_{3})-R_{3}}{L_{2}L_{3}\alpha _{2}(\alpha _{1}-\alpha _{2})}}$.........(182-7.3)

电流方程的拉普拉斯逆变换

因此，(182-7) 的拉普拉斯逆变换为：

$I_{1}(t)={\mathcal {L}}^{-1}\left\lbrace {\frac {A_{0}}{s}}+{\frac {A_{1}}{s+\alpha _{1}}}+{\frac {A_{1}}{s+\alpha _{2}}}\right\rbrace =A_{0}+A_{1}e^{-\alpha _{1}t}+A_{2}e^{-\alpha _{2}t}$.........(182-8)

剩余变量 $I_{2}(t)$ 和 $I_{3}(t)$ 以及相应的电压由公式 (182)、(182-1) 和 (182-2) 确定。

电路动态分析

公式 (182-8) 中的电流 $I_{1}(t)$ 显示了一个与时间无关的成分 $A_{0}$ 以及两个衰减项，当 t 趋于 ∞ 时，这两个衰减项将达到渐近值。换句话说，三个电路中的电流没有正弦振荡，主要是因为：（1）施加的电压是恒定的，（2）电路没有电容元件。

注意： 此示例可以通过多种方式 修改，使其涉及电压脉冲、正弦电压源、电容以及电荷和电流的各种边界和初始条件。

方法的推广

在上面的例子中，可以做以下修改

(1) 基尔霍夫方程中施加的电压可以采用多种形式，例如

• :$E(t)=E_{o}\delta (t)$
• :$E(t)=E_{o}\sin(\omega t)$
• :$E(t)=E_{o}f(t)$

(2) 电容在持续时间内添加电流的积分项，如

• : ${\frac {1}{C}}\int _{0}^{t}I(\tau )d\tau$